Komplexa tal
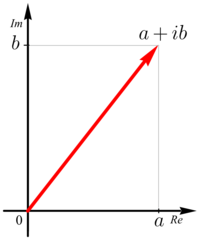
De komplexa talen kan ses som en utvidgning av de reella talen. Ett komplext tal kan skrivas som
där det reella talet a är realdelen, det reella talet b är imaginärdelen och i är den imaginära enheten med egenskapen
Om b ≠ 0 så är z ett icke reellt komplext tal (till exempel 2 + 4i), och om a = 0 kallas talet rent imaginärt (till exempel 4i).[1]
Mängden av komplexa tal betecknas med C[2] eller ℂ, och utgör en kropp.
Definitioner[redigera | redigera wikitext]
De första matematikerna som på 1500-talet började räkna med komplexa tal ansåg att kvadratrötter ur negativa tal egentligen inte fanns, utan var "imaginära" (det vill säga "inbillade"), medan de riktiga talen var "reella" (alltså "verkliga"). Detta språkbruk lever kvar, trots att det sedan länge är känt att komplexa tal är precis lika "verkliga" som de reella talen. Mängden av komplexa tal C kan nämligen formellt definieras med hjälp av enbart reella tal och de vanliga aritmetiska operationerna för dessa. Man definierar då[3] C som mängden R2av ordnade talpar (a, b), där a och b tillhör den reella talmängden R, tillsammans med operatorerna + och ·, vilka ges av föreskrifterna
och
- .
Definierad på detta sätt utgör C en (algebraisk) kropp, i likhet med mängden R av reella tal. Det innebär att de fyra vanliga räknesätten, alltså addition, subtraktion, multiplikation och division, är definierade på C och uppfyller de vanliga reglerna (så att bland annat addition och multiplikation är associativa och kommutativa operationer, multiplikation är distributiv med avseende på addition och subtraktion, och subtraktion respektive division kan ses som addition respektive multiplikation med inversa element).
Till skillnad från de reella talen saknar de komplexa talen en naturlig ordning. De reella talen kan tänkas ordnade på en tallinje, med de mindre talen till vänster om de större talen. De komplexa talen får man i stället tänka sig i ett talplan, där talet (a, b) tolkas som punkten med koordinaterna a och b. Dessa koordinater kallas för realdelen respektive imaginärdelen för talet (a, b). Observera särskilt att både realdelen a och imaginärdelen b är reella tal.
Det komplexa talplanet kallas också för Arganddiagrammet.
Delmängden av de komplexa talen av typen (a, 0) motsvarar de reella talen, så att (a, 0) kan "identifieras med" a och den imaginära enheten i är det komplexa talet (0, 1). Med dessa konventioner och med definitionerna av multiplikation och addition ovan, får man
Alla tal (0, b), det vill säga alla tal b⋅i, sägs vara rent imaginära. De rent imaginära talen blandas ibland ihop med "imaginärdelar", men imaginärdelen av det rent imaginära talet bi är enligt definitionen ovan det reella talet b.
Rektangulär form[redigera | redigera wikitext]
Representationen av ett komplext tal på formen
kallas rektangulär form.
För
är projektionsfunktionerna definierade som
- realdelen av z
och
- imaginärdelen av z.
Polär form[redigera | redigera wikitext]

Enligt Eulers formel gäller
vilket innebär att ett allmänt komplext tal kan skrivas som
där r, absolutbeloppet, är avståndet till origo i det komplexa talplanet och φ är vinkeln mellan den reella axeln och en linje genom origo och talets punkt i det komplexa talplanet.
Vinkeln φ kallas argumentet (arg) för
och bestäms enligt
Intervallet för argumentet är (−π, π], vilket kallas principalargumentet, kan mappas till [0, 2π) genom att 2π adderas till negativa värden. Argumentet kan omfatta alla intervall som är en heltalsmultipel av 2π.
För datorbaserade beräkningar kan det vara lämpligt att använda funktionen atan2(b, a) om denna är implementerad.
Absolutbelopp[redigera | redigera wikitext]
Absolutbeloppet av ett komplext tal z = a + bi kan i det komplexa talplanet tolkas som avståndet från origo till punkten (a, b) och beräknas som
eller
För absolutbeloppet gäller
Konjugat[redigera | redigera wikitext]
Konjugatet till ett komplext tal z = a + bi definieras som
Ett komplext tals konjugat kan bildas genom att spegla dess imaginärdel i x-axeln:
Om talet är givet på polär form kan konjugatet bildas genom teckenbyte för argumentet:
För konjugatet gäller
De reella och imaginära delarna kan extraheras med hjälp av konjugatet:
Räkneregler[redigera | redigera wikitext]


Rektangulär form[redigera | redigera wikitext]
Addition[redigera | redigera wikitext]
De reella och de imaginära delarna adderas var för sig.
Subtraktion[redigera | redigera wikitext]
I analogi med addition, subtraheras de reella och imaginära delarna var för sig.
Multiplikation[redigera | redigera wikitext]
Division[redigera | redigera wikitext]
Exempel:
Bråket förlängs med nämnarens konjugat. Därmed elimineras nämnarens imaginära del och kvoten fås på formen a + bi.
Polär form[redigera | redigera wikitext]
Låt
Då gäller enligt räknereglerna för exponentiella tal
Av detta följer
Exempel: Om z skrivs i polär form som
är n:te roten av z
Övrigt[redigera | redigera wikitext]
För beräkningar utförda för hand är det lämpligt att använda den rektangulära formen för addition och subtraktion och den polära formen för multiplikation och division.
Funktioner av komplexa tal[redigera | redigera wikitext]
De analytiska funktioner som är definierade för de reella talen är också definierade för de komplexa talen. Några av dem är entydigt definierade, andra är flervärda funktioner.
Exponentialfunktionen[redigera | redigera wikitext]
Enligt de kända serieutvecklingarna för reella x av
framgår att exponentialfunktionen ez för komplexa z enligt
kan definieras genom serien
Serien är konvergent för alla z.
Logaritmfunktionen[redigera | redigera wikitext]
Utifrån exponentialfunktionen kan den komplexa logaritmen definieras och är en flervärd funktion.
Den komplexa logaritmen definieras som
och de flesta logaritmlagar som gäller för de reella talen gäller också för den komplexa logaritmen.
Med hjälp av logaritmfunktionen kan till exempel roten av komplexa tal bildas då
vilket lätt kan beräknas.
Observera att med denna definition, erhålls två lösningar även när z är ett reellt tal.
Trigonometriska funktioner[redigera | redigera wikitext]
Trigonometriska funktioner av komplexa tal är entydigt definierade enligt
Funktionernas inverser blir som för reella tal flervärda funktioner.
Seriers konvergens[redigera | redigera wikitext]
Antag en summa av n komplexa tal:
Om följden har ett gränsvärde S är den oändliga serien konvergent med summan S:
Termerna cj kan skrivas
och således
Serien konvergerar, om och endast om, delserierna konvergerar och då är
Matriser[redigera | redigera wikitext]
2×2-matriser av formen
kan användas för att representera komplexa tal där E är en enhetsmatris och matrisen I motsvarar den imaginära enheten. Då gäller
Reella tal motsvaras av diagonalmatrisen
De linjära avbildningar som svarar mot dessa matriser spänner upp ℝ².
Användningsområden[redigera | redigera wikitext]
Komplexa tal är grundläggande för delar av matematiken. Enligt algebrans fundamentalsats har en ekvation av typen p(x) = 0, där p är ett polynom av graden n, exakt n komplexa rötter. Detta medför att de komplexa talen utgör en algebraiskt sluten kropp. Om p endast har reella koefficienter och x är en rot till p(x) = 0, så är även konjugatet till x en rot.
Komplexa tal inom fysiken[redigera | redigera wikitext]
Komplexa tal är mycket användbara inom fysiken, till exempel för att beskriva vågrörelser eller svängningar inom elektromagnetismen. Detta på grund av att man med komplexa tal samtidigt hanterar både absolutbelopp och fasvinkel, vilket är till stor nytta för att beräkna belopp och fasförskjutningar för spänningar och strömmar.
Med jω-metoden (j-omega-metoden) behandlas växelströmsproblem i nära analogi med motsvarande likströmsproblem genom införande av komplexa impedanser.
Inom elektrotekniken används ofta komplexa tal i olika slag av transformer, som till exempel Fouriertransformen och Laplacetransformen, för att underlätta vid beräkningar av växelströmsförlopp.
Inom kvantmekaniken är de grundläggande vågfunktionerna komplexa.
I strömningsmekanik används komplexa funktioner för konforma avbildningar.
Historik[redigera | redigera wikitext]
Under 1500-talet förekom kvadratrötter ur negativa tal i de lösningar till tredje- och fjärdegradsekvationer som upptäcktes av de italienska matematikerna Niccolo Fontana Tartaglia och Gerolamo Cardano. Även om man bara var intresserade av reella lösningar, ledde dessa formler ibland till sådana kvadratrötter som mellanresultat.
Namnet imaginära för sådana tal myntades av René Descartes på 1600-talet och man betraktade dem länge med stor misstänksamhet. Komplexa tal accepterades först efter att deras geometriska tolkning hade beskrivits och publicerats av Caspar Wessel 1799. Denna beskrivning återupptäcktes flera år senare av bland andra Carl Friedrich Gauss. Den moderna definitionen som ett par av reella tal infördes under 1800-talet av William Rowan Hamilton.
Flera av Leonhard Eulers mest betydande upptäckter vilar väsentligt på införande av komplexa tal. Abels skapelse, de elliptiska funktionerna, förde än mer de komplexa talen i förgrunden inom matematisk forskning. Så blev ytterligare fallet, när den moderna funktionsteorin framväxte ur Abels, Cauchys, Weierstrass och Riemanns arbeten.
Carl Friedrich Gauss och Karl Weierstrass arbeten har visat, att införande av högre komplexa tal, bildade av flera än två grundenheter, inte medför fördelar jämförliga med dem som vinns genom införande av de av två grundenheter bildade komplexa talen.[4]
Likheter och skillnader med vektorer[redigera | redigera wikitext]
Komplexa tal och tvådimensionella reella vektorer adderas enligt samma regler (är isomorfa under addition), absolutbeloppen är desamma, och båda kan skalas med ett reellt tal.
Vektorer har en inre produkt som är ett reellt tal. För komplexa tal är det enkelt att skapa en funktion motsvarande skalärprodukten, men en sådan är inte en bärande del av de komplexa talens struktur. En möjlig sådan funktion är
- .
Den viktigaste skillnaden är att multiplikation inte är definierad för vektorer i den meningen att en multiplikation av två vektorer resulterar i en tredje vektor.
Se även[redigera | redigera wikitext]
| Den här artikeln ingår i boken: Matematik |
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Weisstein, Eric W., "Complex Number" (engelska), MathWorld.
- ^ http://www.math.kth.se/~skjelnes/KURS/GYMNAS/10/Forelesning220311Gymnas.pdf
 PDF
PDF
- ^ ”Komplexa tal”. http://www.users.abo.fi/togustaf/DiffE/KomplexaTal.pdf. Läst 14 oktober 2013.
 PDF
PDF
- ^ Komplexa tal i Nordisk familjebok (andra upplagan, 1911)
Källor[redigera | redigera wikitext]
- Complex Analysis for Mathematics and Engineering av John H. Mathews & Russel W. Howell
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Komplexa tal.
Wikimedia Commons har media som rör Komplexa tal.
| |||||
| ||||||||||||||
|









































![{\displaystyle {\sqrt[{n}]{z}}={\sqrt[{n}]{r}}\left(\cos {\frac {\varphi }{n}}+\mathrm {i} \,\sin {\frac {\varphi }{n}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dd13b8c209598a93509b3883922b7d08d3c2354)
























