Inversion
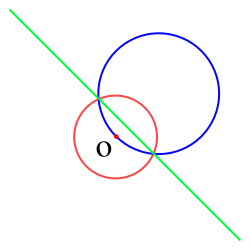
Inversion i planet är, löst uttryckt, ett sätt att spegla geometriska objekt i en given cirkel, den så kallade inversioncirkeln. Inversion innebär alltså att man vänder objekt innanför cirkeln, så de hamnar utanför cirkeln och tvärtom. Objekt som ligger helt på inversionscirkeln, kommer att övergå i objekt som fortfarande ligger på inversionscirkeln.
Medan inversion (lokalt) bevarar vinklar, förvanskas dock längder och bland de få objekt som har enkla utseenden både före och efter inversion finns linjer (som övergår i linjer eller cirklar) och cirklar (som övergår i linjer eller cirklar). Därför kan inversiv geometri ses som en formalisering av den transparenta och intuitiva observationen att linjer kan betraktas som "cirklar med oändlig radie".
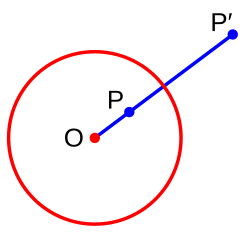
Grunden för inversion av geometriska objekt är inversion av punkter. Två punkter A och B sägs vara inversiva punkter till varandra med avseende på cirkeln med centrum O och radie r om
Genom likformighet kan man till exempel visa vända-ut-och-in egenskapen samt att vinklar bevaras som nämndes ovan.
Man kan på analogt sätt även införa inversion i rummet.
Inversion "uppfanns" av Jakob Steiner cirka 1830 och behandlas rätt smidigt i kartesianska koordinatsystem genom att representera punkter (vektorer) som komplexa tal. Typiskt utseende på inversion ges då av Möbiusavbildningen
För att kunna undersöka något djupare egenskaper hos inversion, visar det sig lämpligt använda resultat och metoder från den komplexa analysen. Faktum är, att inversion numer oftast studeras på högskolenivå som en del i kurser i komplex analys.
Möbiustransformationer kan visas bilda en grupp. Och enlighet med Felix Kleins Erlangenprogram, att geometri är studium av symmetrigruppen hos vissa funktionsklasser, kommer inversion att bilda en egen geometri, så kallad inversiv geometri.
Vissa geometriska problem som behandlar cirklar och linjer och vid första anblick verkar svåra kan lösas genom att utföra en lämplig inversion varpå resultatet följer. Ett exempel på detta är Steiners porism.
Inversion har även kopplingar till icke-euklidisk geometri.


