Mätbar funktion

En mätbar funktion är inom matematiken en speciell sorts funktion mellan mätbara rum som bevarar mätbarheten.

Formell definition

För en mätbar funktion är den inversa bilden av en mätbar mängd också mätbar.

Låt $(X,\mathcal{F})\,$ och $(Y,\mathcal{G})\,$ vara mätbara rum.

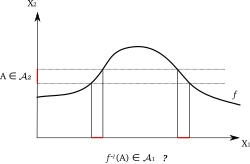
En funktion $f: X \rightarrow Y$ är mätbar om

$f^{-1} (G) \in \mathcal{F}\,$

för alla $G \in \mathcal{G}\,$.

Man kan också säga att en funktion är $\mathcal{F}\,$-mätbar eller $(\mathcal{F},\mathcal{G})\,$-mätbar.

Notera att man inte behöver ha något mått definierat på rummen för att avgöra om en funktion är mätbar.

Lebesguemätbar funktion

Om $(Y,\mathcal{G}) = (\R,\mbox{Leb}\,\R)\,$ kan man också säga att en mätbar funktion är Lebesguemätbar.

Borelfunktion

Låt

$\overline{\R}:=\R\cup \{ -\infty, +\infty \}.$

Om X är ett topologiskt rum, $(X,\mathcal{F}) = (X,\mbox{Bor}\,X)\,$ och $(Y,\mathcal{G}) = (\overline{\R},\mbox{Bor}\,\overline{\R})\,$ så kallas en mätbar funktion

$f: X \rightarrow \overline{\R}$

för Borelfunktion.

Eftersom Borelmängder är genererad av öppna mängder kan man bevisa att en funktion $f: X \rightarrow \R \cup \{ -\infty, +\infty \}$ är en Borelfunktion om och endast om

$f^{-1} (G)\,$, $f^{-1} (\{ -\infty \} )\,$ och $f^{-1} (\{ +\infty \} )\,$ .

är Borelmängder för alla öppna mängder $G \subset \mathbb{R}$

Alternativt, en funktion $f: X \rightarrow \overline{\R}$ är en Borelfunktion om och endast om

$\lbrace x \in A : f(x) > c \rbrace$

är Borelmängder för alla $c \in \R$.

Exempel

Alla kontinuerliga funktioner i $\R^n$ är Lebesguemätbara och Borelfunktioner.

Se även

• Mått
• Borelmängd
• Lebesgueintegration
• Denna artikel ingår i en bok om Måtteori. PDF-version

Källor

• G.B. Folland, Real analysis: Modern techniques and their applications, Second edition, Wiley interscience, (1999)