Handelsresandeproblemet
Handelsresandeproblemet (engelska: the Traveling Salesman Problem, TSP) är ett matematiskt problem inom den del av optimeringsläran som behandlar optimering i grafer. Enkelt uttryckt går problemet ut på att hitta den kortaste vägen för en handelsresande som ska besöka en uppsättning städer. Det kan emellertid istället gälla den snabbaste vägen eller den billigaste eller optimum enligt något annat kriterium. Frågeställningen är vanlig i GIS-analyser som hanterar ruttplaneringsproblem och nätverksanalyser.
Handelsresandeproblemet formulerades första gången på 1850-talet av matematikerna William Rowan Hamilton och Thomas Penyngton Kirkman.
Allmänt[redigera | redigera wikitext]
Handelsresandeproblemet är ett vanligt förekommande matematiskt problem. Varianter av handelsresandeproblemet förekommer i princip överallt där transportsträckor förekommer, långa eller korta, så som vid borrning av kretskort och vid resor mellan ett antal orter.
Att forska på handelsresandeproblemet är populärt, och artiklar om just detta har alltid rönt långt större intresse hos allmänheten än vad andra optimeringsproblem har gjort. Orsaken till dess popularitet och allmänintresse ligger delvis i problemets enkla definition, vilket gör problemet begripligt även för personer helt utan någon matematisk skolning, även för förskolebarn. Ett handelsresandeproblem är enkelt att definiera, men utgör likafullt en av de svåraste typerna av optimeringsproblem, då det gäller att finna en bevislig, matematisk optimalitet (optimal lösning). Problemets grundläggande frågeställning är att hitta snabbaste vägen mellan ett antal orter.
Ett "handelsresandeproblem" uppstår då ett visst antal punkter (noder) i godtycklig ordning skall besökas med minsta möjliga kostnad i form av tid, pengar, resväg eller vad som helst som är mätbart. Vad som skall utföras på de olika punkterna är helt ovidkommande för själva problemets lösning.
Varje gång en transportrutt av något slag skall planeras eller exempelvis en robots rörelser skall automatiseras (inför punktsvetsning, placering av komponenter på kretskort, på en bil etc), dyker ett handelsresandeproblem upp i någon form.
Även privatpersoner stöter på problemet när de planerar en resa eller när de ska handla varor i en större matbutik.
Formell beskrivning[redigera | redigera wikitext]
Handelsresandeproblemets definition är: ”Finn den billigaste Hamiltoncykeln i en given graf med bågkostnader”. Bågkostnader ("transportkostnader" inom en graf) behöver inte vara kostnader, det kan också vara sträcka eller tid, allt beroende på vad som skall optimeras.
I det klassiska handelsresandeproblemet skall varje nod besökas en enda gång. Det finns emellertid en variant där återbesök tillåts (varje nod skall således besökas minst en gång). Denna typ av handelsresandeproblemet förkortas vanligen TSPr.
Ytterligare en speciell variant av handelsresandeproblemet är, då noderna är uppdelade i två grupper dels en grupp som skall besökas, dels en grupp som får besökas men som inte måste besökas. Det är tillåtet att ta vägen över en nod som får besökas på vägen till en nod som skall besökas.
Handelsresandeproblem behandlas normalt i oriktade grafer (det vill säga man får gå både från A till B och från B till A), men de förekommer även i riktade grafer (man får gå antingen från A till B eller från B till A men inte i båda riktningarna). De metoder som används för att lösa handelsresandeproblem är normalt endast definierade (giltiga) i oriktade grafer.
Världens största handelsresandeproblem[redigera | redigera wikitext]
Rekordet för antalet noder, för vilka transportvägarna är lösta, ligger för tillfället på 85 900 noder. Det uppnåddes i april 2006 av forskarna William Cook, David Applegate, Robert Bixby, Vašek Chvátal, Keld Helsgaun, Daniel Espinoza och Marcos Goycoolea som löste uppgiften med hjälp av programmet Concorde TSP Solver. De fem förstnämnda forskarna löste för övrigt den 20 maj 2004 ett problem med 24 978 noder, efter att ha arbetat med det i ungefär tre år. Noderna i problemet var Sveriges 24 978 orter. Resultatet blev att den som har för avsikt att besöka Sveriges samtliga orter måste resa cirka 72 500 km.[1]
När så här stora problem ska lösas används flera olika metoder parallellt med varandra. En del av metoderna måste kanske användas flera gånger, för att den föregående metoden inte visade sig ge godtagbara resultat. Mycket av bevisbördan ligger i att kunna visa, att den lösning som de optimerade metoderna fått fram verkligen är en optimallösning och inget annat.
Lösningsmetoder[redigera | redigera wikitext]
Handelsresandeproblem är svåra att lösa, redan vid 10 noder är det normalt svårt att direkt se den optimala turen. Att helt enkelt testa alla möjliga lösningar på ett givet problem är visserligen i princip möjligt, men antalet test ökar med fakultets funktion (exempel på fakultet: 5‑fakultet = 5! = 1·2·3·4·5 = 120) beroende av antalet bågar och noder där n är totala antalet noder och m är totala antalet bågar. Därför är det oftast inte praktiskt möjligt att ens med superdatorer testa alla möjliga lösningar vid problem med ett mycket stort antal noder. Andra metoder måste tillgripas.
Eftersom handelsresandeproblem är erkänt svårlösta, har det utvecklats flera olika metoder för att lösa dem. Dessa metoder kan delas upp i två grupper. Den ena gruppen innehåller metoder som hittar den optimala lösningen. Den andra gruppen innehåller metoder som åtminstone finner en tillåten lösning. Den senare metodtypen kallas för 'en heuristik' (lite vårdslöst skulle man kunna ersätta ordet med 'en chansning').
Heuristiker hittar normalt inte den optimala lösningen och de lösningar de vanligtvis levererar ger inga uppgifter om hur bra eller dålig lösningen är, men de ger åtminstone en lösning. Denna kan emellertid lika väl vara den sämsta som den bästa. Trots heuristikens alla nackdelar har den en stor fördel som gör den intressant vid lösandet av optimeringsproblem. Den är nämligen mycket snabb i förhållande till den förstnämnda metodtypen. Är snabbhet en viktig faktor vid lösandet, väljs normalt en heuristisk metod.
När det gäller de optimerande metoderna, finns det flera att välja bland. En del av dessa är mycket generella (oftast är kravet att valensen är minst två för alla noder (valensen för en nod är det antal bågar som har sin ändpunkt i noden[2])) och fungerar på flertalet handelsresandeproblem. Andra är sådana som utnyttjar en speciell egenskap i det aktuella handelsresandeproblemet, som därmed kan göra just det problemet lättare att lösa.
Eftersom handelsresandeproblem är svårlösta brukar problemen utsättas för så kallad förbehandling. Förbehandling har flera syften: det ena är att minska problemets komplexitet, det andra är att förbereda problemet för den optimeringsmetod som ska användas – optimeringsmetoden kan till exempel ställa krav på att alla noder ska ha minst valens två för att fungera – det tredje syftet är att försöka utröna om det över huvud taget finns någon lösning på det aktuella optimeringsproblemet.
Matematiskt optimerande metoder[redigera | redigera wikitext]
Alla Hamiltoncykler (handelsresandeturer) är så kallade 1-träd, men för att 1‑träd ska vara en Hamiltoncykel, måste varje nod i cykeln ha valens 2. Detta samband utnyttjar flera olika metoder för att lösa handelsresandeproblem. Två metoder som använder 1-träd för att lösa handelsresandeproblem är dels metoden att addera straffkostnader till bågar som ansluter till en nod med för hög valens, dels trädsökningsalgoritmer (en algoritm är en matematisk procedur, en sorts mall, som försöker lösa ett givet problem).
Metod med straffkostnader[redigera | redigera wikitext]
Algoritmen med addering av straffkostnader är som visas nedan.[3]
| Steg | Att göra |
|---|---|
| 1 | Finn billigaste uppspännande 1-träd. |
| 2 | Stoppa om en Hamiltoncykel hittas. |
| 3 | Välj en nod med för hög valens. Öka kostnaderna för alla bågar som ansluter till noden med exempelvis 1. |
| 4 | Gå tillbaka till steg 1. |
Metoden är enkel men har en allvarlig begränsning: den kan hamna i en evighetsslinga, en så kallad cykling. Detta kan inträffa om två noder omväxlande får för hög valens. En annan nackdel med metoden är, att om kostnaderna för bågarna varierar stort, kan det ta många iterationer (upprepningar) och därmed lång tid för metoden att finna en lösning.
Exempel[redigera | redigera wikitext]
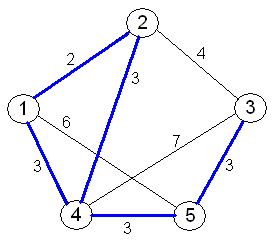
Initialt ser problemet ut som ovan.
Först skall det billigaste uppspännande 1-träd (steg 1 i algoritmen) sökas. Därefter konstateras att det inte rör sig om en Hamiltoncykel (steg 2) varför processen går vidare till steg 3 i algoritmen. Då konstateras att nod 4 har valens 3, och följaktligen ökar kostnaderna för alla bågar som ansluter till nod 4 (se nästa bild).
Algoritmens steg upprepas, och det är nu klart att alla noder har valens 2. Därmed finns det en Hamiltoncykel, det vill säga lösningen är funnen.
Metod som använder trädsökning[redigera | redigera wikitext]
Denna metod är mer avancerad än den ovan beskrivna (som adderar straffkostnader), och den belastas inte av de svagheter som metoden med straffkostnaderna har.
Metoden bygger på att problemet initialt delas upp i delproblem så att dessa bildar en trädstruktur. Därefter beräknas undre och övre gränser för problemet, för att svaret inte skall omfatta alla tänkbara lösningar. Dessa gränser används för att avgöra vilka delproblem som är intressanta att undersöka vidare. Vidare avbryts undersökningen av delproblemet om en lösning på problemet saknas, eller om en Hamiltoncykel erhålles.
Metoden finner ett optimum som är matematiskt säkerställt, och den kan inte hamna i cykling. Är det inte ett krav att hitta ett optimum, kan beräkningen istället avbrytas när en tillräckligt bra lösning har hittats.
Exempel[redigera | redigera wikitext]
Samma graf som i exemplet med straffkostnader används även här.
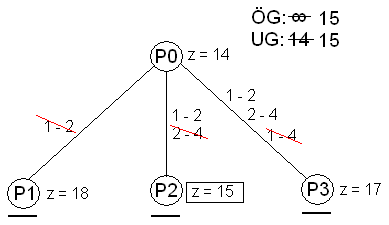
P0 (grundproblemet): Först skall billigaste 1-träd hittas. Om detta hade bildat en Hamiltoncykel, hade problemet varit löst i och med detta. Om inte, så vidtar arbetet med att dela upp problemet i delproblem (P1, P2 och så vidare).
Övre gränsen (ÖG) bestäms av den senast funna lösning som för tillfället är den bästa. Eftersom ingen lösning finns vid inledningen, är övre gränsen då lika med plus oändligheten. Undre gränsen (UG) bestäms med hjälp av uträkningar antingen i huvudproblemet eller i delproblemet, vilka garanterat ger ett värde som inte är högre än den optimala lösningen. Som en första undre gräns använd normalt värdet av ett 1-träd, det vill säga normalt värde av PO (z=14).
När övre och undre gränser är klara, vidtar arbetet med att bilda delproblem. I P0 framgår att en cykel föreligger, vilken omfattar tre bågar ([1-2], [2-4], [1-4]). Eftersom cykeln omfattar tre bågar bildas tre delproblem P1, P2 och P3. I P1 får båge [1-2] inte användas. I P2 skall båge [1-2] användas medan båge [2-4] inte får användas. I P3 skall bågarna [1-2] och [2-4] användas medan båge [1-4] inte får användas. Nu skall alla delproblemen lösas på den första nivån i trädet (P1, P2 och P3).
P1: Lösning enligt ovan erhålls där båge [1-2] är förbjuden att användas. Lösningen på 1-trädet är 18 (z = 18), och en ny cykel ([1-4], [4-5], [1-5]) föreligger.
P2: Lösning enligt ovan erhålls där båge [1-2] är medtvingad och båge [2-4] är förbjuden. Lösningen på 1-trädet är detta fall 15 (z = 15), och lösningen är en Hamiltoncykel det vill säga en giltig handelsresandetur.
P3: Lösning enligt ovan erhålls där båge [1-2] och [2-4] är medtvingad och båge [1-4] är förbjuden. Lösningen på 1-trädet är 17 (z = 17), och en ny cykel ([1-2, [2-4], [4-5], [1-5]) föreligger.
Nu är delproblemen på första nivån i delproblemträdet lösta. För det första är z lika med 18, 15 respektive 17 för P1, P2 respektive P3, därför kan undre gränsen som lägst vara 15, och UG uppdateras. Eftersom en Hamiltoncykel hittades i P2 med värdet 15 uppdateras även ÖG, varvid optimum är instängt (vilket i praktiken innebär att optimallösningen är hittad).
P2 är enkel eftersom lösningen hittades. Där behöver inget mer göras. Grenen kan då "kapas" som det heter på fackspråk. I just detta problem är z större i P1, P2 och P3 än vad z är i P0. Detta är ingen slump. Värdet z i P1, P2 och P3 kan som lägst bli 14 i det här exemplet. Detta medför en viktig konsekvens för vad som skall göras med P1 och P3. P1:s z‑värde är lika med 18. Det innebär att om P1 delas upp i nya delproblem och en ny Hamiltoncykel hittas, så är den nya cykeln inte bättre än 18, det vill säga dess lösning är sämre än den som redan hittats i P2. Därför kapas alla grenar som har större eller lika stort värde på z som ÖG. Det vill säga både P1 och P3 kapas. Nu har trädet inga återstående förgreningar att undersöka – optimallösningen är funnen.
Vad hade hänt om P1:s z‑värde varit 14 till exempel? Jo, det hade då varit nödvändigt att dela upp P1 i nya delproblem, närmare bestämt tre stycken, P4, P5 och P6. Dessa delproblem hade ärvt kravet att båge [1-2] är förbjuden. P4 hade alltså fått ärva kravet att bågarna [1-2] och [1-4] är förbjudna. Samma krav hade därefter måst sättas upp för P5 och P6. Om P4 hade beräknats, skulle en lösning aldrig ha hittats, på grund av att nod 1 bara har en tillåten båge kvar (den har valens 1).
Därför kapas grenar i sökträdet om;
| 1. grenens z är större än eller lika med ÖG |
| 2. om grenen saknar lösning |
| 3. om grenen har en lösning. Om lösningen är bättre än ÖG uppdateras ÖG och lösningen sparas. Grenar som tidigare visat sig vara intressanta att undersökas, kontrolleras om de fortfarande är intressanta, annars kapas de (steg 1 ovan). |
Om inte grenen kapas, förgrenas den, och förfarandet ovan upprepas tills alla grenar som är intressanta att undersöka är genomsökta. När detta är klart, har en optimal lösning hittats, det vill säga om en dylik alls finns.
De över och undre gränserna kan också användas för att avgöra om det är värt besväret att leta vidare. Den lösning som redan hittats kan vara tillräckligt bra. Även om den inte nödvändigtvis är optimal, kanske den inte ligger längre från optimum än högst några procent. Det kan hända att man vid analysen finner, att det inte är så viktigt att hitta den optimala lösningen. Kanske räcker det med att den lösning som erhålls är tillräckligt bra, att den exempelvis ligger 5 procent från optimum (ÖG/UG ≤ 1,05).
Metod som använder heuristik[redigera | redigera wikitext]
Det finns ett antal metoder som använder heuristik. Nedan visas en som använder simulerad evolution.
Exempel på lösning med simulerad evolution[redigera | redigera wikitext]
[4] Detta enkla exempel visar hur den evolutionära principen med cyklisk repetition av slumpvariation och urval kan bidra till lösningen av mycket svåra problem.
Antag att en handelsresande skall göra en rundtur till 60 städer. För den simulerade evolutionen är detta som att ha en population av kortlekar (individer) där varje kortlek har 60 kort numrerade (helst på båda sidor) från 1 till och med 60. Antalet valbara rundturer blir i detta fall lika med antalet olika sätt att blanda en kortlek med 60 kort, det vill säga den blir av samma storleksordning som det totala antalet atomer i universum (vilka uppskattats till ett antal av en etta följd av 80 nollor). Så, att finna den bästa lösningen, eller ens en någorlunda bra lösning, genom att slumpmässigt blanda korten är i det närmaste omöjligt.
Med simulerad evolution blir situationen helt annorlunda. Den naturliga evolutionen använder ibland en inversionsoperator, som i princip kan ta ut en bunt kort ur leken, vända den ett halvt varv och sätta tillbaks den igen som figuren nedan visar.
När denna inversion råkar inträffa där rundturen bildar en ögla, kommer öglan att upplösas och rundturen blir garanterat kortare. Sannolikheten att detta skall inträffa är större än 1/(60*60) om vi har 60 städer, så öglor kommer att försvinna då och då. En simulering startades med följande rundtur.
Efter en simulering med 1500 generationer, med en population av 180 kortlekar där 60 selekterades, har alla öglor försvunnit, och följande rundtur har påträffats. Det mänskliga ögat kan lätt upptäcka att smärre förbättringar kan göras, men den erhållna lösningen är kanske bara någon procent sämre än den optimala, vilket ofta är gott nog.
I det speciella fall då alla städer ligger längs utefter en cirkelperiferi med utgångspunkten i cirkelns mittpunkt, kommer algoritmen att finna den optimala lösningen när samtliga öglor har avlägsnats. Det vill säga denna enkla slumpalgoritm kan finna den optimal lösningen bland 10 upphöjt till 80 möjliga lösningar.
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
- ^ ”Traveling Salesman Problem”. Georgia Institute of Technology. Arkiverad från originalet den 7 februari 2006. https://web.archive.org/web/20060207171845/http://www.tsp.gatech.edu/. Läst 16 februari 2008. (engelska)
- ^ ”Block 6 Algebra och Diskret Matematik A; Grafteori”. Mittuniversitetet. Arkiverad från originalet den 19 februari 2007. https://web.archive.org/web/20070219172210/http://www.tfm.miun.se/~piahei/adm/res/block6.html.
- ^ [a b] Kaj Holmberg, Kombinatorisk optimering med linjärprogrammering, 2006, Matematiska Institutionen Linköpings tekniska högskola.
- ^ Goldberg, D. E. Genetic Algorithms in Search, Optimization & Machine Learning. Addison-Wesley, New York, 1989.
Externa länkar[redigera | redigera wikitext]
- ”Traveling Salesman Problem”. Georgia Institute of Technology. http://www.tsp.gatech.edu/. (engelska)