Naturlig transformation

Inom matematik, närmare bestämt kategoriteori, är en naturlig transformation något som avbildar en funktor på en annan funktor, på ett sådant sätt att strukturen hos de inblandade kategorierna bevaras. Med andra ord kan man se en naturlig transformation som en "morfism mellan funktorer".

Definition

Låt $F$ och $G$ vara kovarianta funktorer mellan kategorierna ${\mathcal {C}}$ och ${\mathcal {D}}$. En naturlig transformation från $F$ till $G$ är en funktion som till varje objekt $X\in {\mathcal {C}}$ tilldelar en ${\mathcal {D}}$-morfism $\eta _{X}:F(X)\to G(X)$ sådan att för varje morfism $f:X\to Y$ i ${\mathcal {D}}$ gäller det att $\eta _{Y}\circ F(f)=G(f)\circ \eta _{X}$. Detta kan också skrivas med hjälp av ett kommutativt diagram som:

Diagrammatisk definition av naturlig transformation

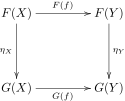
Definitionen kan också dualiseras: om $F$ och $G$ istället är kontravarianta funktorer så är en naturlig transformation motsvarande kommutativa diagram där de horisontella pilarna pekar i motsatt riktning.

Exempel

Ett typiskt exempel på en naturlig transformation kommer från linjär algebra: Låt A = B = Vec _K vara kategorin av (ändligtdimensionella) vektorrum över en kropp K. Om F nu är identitetsfunktorn på Vec _K och G är funktorn som avbildar varje vektorrum V på sin bidual V**, så finns det en naturlig transformation som till varje objekt i A, alltså till varje vektorrum V, tilldelar avbildningen $T_{V}:V\rightarrow V^{**}$, där T _V definieras av $(T_{V}(x))(f)=f(x)$. Inom linjär algebra säger man vanligen att det finns naturlig isomorfism mellan V och V**. Detta innebär precis att T är en naturlig transformation från identitetsfunktorn F till "dubbeldualfunktorn" G.