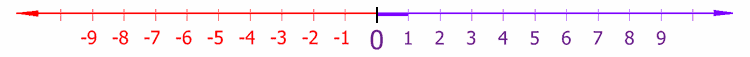Tal

Matematiska begrepp
Tal Mängd Variabel Ekvation Funktion Operator Vektor Linjärt rum

Delmängder till komplexa tal.

Tal är ett matematiskt grundbegrepp som används för att representera olika storheter, det vill säga sådant som går att mäta i bestämda måttenheter, till exempel antal, längd, vikt, volym, temperatur och tryck.

Ett tal är en abstrakt enhet som representerar ett antal eller ett mått. Inom matematiken är definitionen av tal vidare och inkluderar bland annat naturliga tal, heltal, negativa tal, rationella tal, reella tal och komplexa tal med mera.

Aritmetik, "räknelära", behandlar räknande och innefattar grundläggande egenskaper hos tal, som hur de skrivs och hur de fungerar under addition, subtraktion, multiplikation och division; även andra räkneoperationer som procenträkning, potenser, rotutdragning och logaritmer tillhör aritmetiken. Algebra kan definieras som en utvidgning av aritmetiken och kan beskrivas som förhållanden, vilka uppkommer, när ett ändligt antal räkneoperationer utförs på en ändlig mängd av tal.

Talteori rör främst heltalens egenskaper, men har utvecklas till att bli en vedertagen teknik för att angripa problem även inom andra grenar av matematiken. Talteori kan uppdelas i flera områden beroende på metoderna som används och problemen som undersöks.

Tal ska inte förväxlas med siffra eller nummer som har helt andra funktioner. Ibland kallas räkneuppgifter för "tal", då i meningar som Löste du talet?

Typer av tal

Tal brukar delas in i fem grundläggande grupper (mängder):

Grundläggande

$\mathbb {N}$	Naturliga tal	0, 1, 2, 3, 4, … eller 1, 2, 3, 4, …
$\mathbb {Z}$	Heltal	..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, ...
$\mathbb {Q}$	Rationella tal	a⁄b där a och b är heltal och b inte är 0
$\mathbb {R}$	Reella tal	Gränsen för en konvergent följd av rationella tal
$\mathbb {C}$	Komplexa tal	a + bi eller a + ib där a och b är reella tal och i är imaginära enheten

De naturliga talen är en delmängd av heltalen det vill säga alla naturliga tal är även heltal, skillnaden i detta fall är att heltalen även innefattar negativa tal. Heltalen i sin tur är en delmängd av de rationella talen, de rationella talen är en delmängd av de reella talen, och de reella talen är en delmängd av de komplexa talen.

(För olika metoder att uttrycka tal med symboler, såsom de Romerska siffrorna, se talsystem.)

Naturliga tal

Naturliga tal används för att räkna föremål, till exempel äpplen, så länge de är hela.

Naturliga tal är de icke-negativa talen {0, 1, 2, 3, …} eller alternativt de positiva talen {1, 2, 3, …}. Den förra definitionen är vanlig i Sverige och allmänt i matematisk logik, mängdlära och beräkningsvetenskap, medan den senare kan hittas i bland annat amerikansk litteratur och bland talteoretiker.

Mängden av de naturliga talen betecknas ℕ (eller, av vissa typografiska skäl kan ett vanligt N i fetstil användas).

Mängden av de naturliga talen är diskret, uppräkneligt oändlig och har kardinalitet Alef-noll (ℵ₀).

Enligt den definition som görs i Matematikterminologi i skolan, utgiven av Statens skolverk i Sverige, ingår talet 0 bland de naturliga talen. Konventionen att räkna 0 bland de naturliga talen förekom inte alls före 1800-talet och tillämpas inte av alla matematiker. Den infördes i samband med att de naturliga talen gavs en mängdteoretisk definition, enligt vilken de naturliga talen precis motsvarar kardinaltalen för ändliga mängder och 0 måste användas som kardinaltal för den tomma mängden.

En fördel med att inkludera 0 är att de naturliga talen då utgör en monoid under både addition och multiplikation. En nackdel är att man inom talteori måste göra undantag för 0 i samband med primtalsfaktorisering, då 0 inte kan primtalsfaktoriseras (1 kan faktoriseras som den tomma produkten).

För att undvika förvirring kan ℤ₊ användas för att beteckna de positiva heltalen, och ℕ₀ för de icke-negativa.

Heltal

Heltal innefattar talet noll (0) samt de positiva och negativa talen {…, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, …}, och är därav unionen av mängden av de naturliga talen.

Mängden av heltalen betecknas ℤ (eller, av vissa typografiska skäl kan ett vanligt Z i fetstil användas), från det tyska ordet Zahlen (som betyder "tal").

Mängden av heltalen är uppräknelig och har kardinaltalet Alef-noll.

Ibland definierar man delmängder av ℤ: ℤ⁺, ℤ^* och ℤ^–.

• ℤ⁺ är {1, 2, 3, 4, 5, …}
• ℤ^* är {0, 1, 2, 3, 4, 5, …}
• ℤ^– är {…, -5, -4, -3, -2, -1}

Beroende på definition kan endera ℤ⁺ eller ℤ^* vara detsamma som mängden naturliga tal.

När det gäller datorsystem används termen heltal (de hela talen) som distinktion till flyttal (de reella talen) eftersom de i datorer hanteras, beräknas och lagras olika.

Rationella tal

Rationella tal är de tal som kan skrivas som en kvot (ett bråk) av två heltal:

${\frac {T}{N}}$

där heltalet T är bråkets täljare och heltalet N bråkets nämnare.

Mängden av de rationella talen betecknas ℚ (eller, av vissa typografiska skäl kan ett vanligt Q i fetstil används).

Ett alternativt sätt att uppfatta denna mängd är som mängden bestående av alla lösningar (x) till ekvationer bx - a = 0, där a och b är heltal och b inte är lika med noll.

Sedd som en delmängd av de reella talen utgör de rationella talen en tät mängd; detta innebär att det alltid finns fler rationella tal mellan två olika rationella tal, och att varje reellt tal kan approximeras godtyckligt väl med ett rationellt tal.

Mängden av de rationella talen är uppräknelig, vilket innebär att det i viss mening finns lika många rationella tal som det finns heltal. Detta kan tyckas vara motsägelsefullt, eftersom mängden av alla heltal är en äkta delmängd av ℚ; Detta följer av den första räkneregeln för bråktal som vi härledde ovan: a/1 = a där a är ett heltal.

Det faktum att man kan koppla samman varje rationellt tal med ett unikt heltal, och vice versa, gör att kardinaltalet för ℚ är lika med kardinaltalet för ℤ (mängden av alla heltal). På matematiskt språk säger man att det existerar en bijektiv avbildning mellan mängderna ℚ och ℤ.

Reella tal

Reella tal innefattar de tal som man vanligtvis menar med tal. De kan beskrivas som alla punkter på en kontinuerlig linje, utan att det finns glapp mellan talen i linjen. Denna linje brukar kallas den reella tallinjen.

Mängden av de reella talen betecknas ℝ (eller, av vissa typografiska skäl kan ett vanligt R i fetstil användas).

Mängden av de reella talen är överuppräknelig och har kardinalitet 2^ℵ₀, där ℵ₀ är antalet naturliga tal. Enligt kontinuumhypotesen är detta detsamma som ℵ₁ (Alef-ett).

De reella talen skrivs ofta som avkortade decimalutvecklingar, det vill säga som approximationer, till exempel 3,3333… och 1,4142… där uteslutningstecknet (…) indikerar att flera siffror följer för en mera precis bestämning av talet. De naturliga talen (ℕ) och heltalen (ℤ) är en delmängd av de reella talen där decimaldelen är noll.

De rationella talen (ℚ) är en delmängd av de reella talen, där decimalföljden efter ett tag börjar följa ett periodiskt mönster. Till exempel är 1/3 = 0,333…, 1/11 = 0,09090909…, 2/7 = 0,285714285714…, 95/14 = 6,7857142857142… och de kan skrivas som ett bråk med heltal i täljare och nämnare. Reella tal som inte är rationella kallas irrationella tal.

Exempel på reella tal är 0, 1 (naturliga), 1/2 (rationellt), ${\sqrt {2}}$ (irrationellt, algebraiskt) och $e$ och $\pi$ (irrationella och transcendenta).

Komplexa tal

Det komplexa talplanet. Varje komplext tal representeras av en realdel (Re) och en imaginärdel (Im).

Komplexa tal kan ses som en utvidgning av de reella talen. Ett komplext tal kan skrivas som

$z\ =a+b\,\mathrm {i}$

där det reella talet a är realdelen, det reella talet b är imaginärdelen och i är den imaginära enheten som definieras av

$\mathrm {i} ^{2}\ ={-1}$

Om b ≠ 0 så är z ett icke reellt komplext tal (till exempel 2 + 4i), och om a = 0 kallas talet rent imaginärt (till exempel 4i).

Mängden av komplexa tal betecknas med ℂ (eller, av vissa typografiska skäl kan ett vanligt C i fetstil användas).

Andra typer

Det finns även andra delmängder av tal:

• Negativa tal – Negativa tal är de tal som är mindre än 0, och skrivs med ett minustecken framför, till exempel −1. De tal som är större än 0 kallas positiva tal. Talet 0 självt är varken negativt eller positivt. Mängden av alla negativa tal betecknas ibland Z⁻. Unionen av Z⁻, {0} och Z⁺ är lika med mängden av alla heltal (Z), och {Z⁻, {0}, Z⁺} sägs vara en partition av Z.

• Irrationella tal – Irrationella tal är tal som inte kan uttryckas som bråk, det vill säga tal som inte kan skrivas som a/b, där a och b är heltal. Dess motsats är rationella tal. De irrationella talen är de tal som på decimalform har en oändlig följd av decimaler som inte består av ett oändligt antal periodiska upprepningar. Därav är pi ett exempel på ett irrationellt tal. Ett irrationellt tal är antingen ett algebraiskt tal eller ett transcendent tal. De irrationella talens kardinalitet är kontinuums mäktighet. Informellt uttryckt betyder det att nästan alla reella tal är irrationella.

• Imaginära tal – Imaginära tal är tal vars kvadrat är ett negativt reellt tal. Termen myntades av René Descartes på 1600-talet och syftar till att man då menade att sådana tal inte kan existera. Anledningen till att man införde begreppet är att det ofta finns behov av att räkna med en storhet som har två från varandra oberoende (ortogonala) egenskaper som kan representeras av ett komplext tal vilket består av en realdel och en imaginärdel. Med hjälp av komplexa tal kan man till exempel överföra förhållanden mellan strömstyrkor och spänningar i tidplanet till motsvarande fasskillnader. Imaginära enheten är det tal som är lika med kvadratroten ur −1.

• Transcendenta tal – Transcendenta tal är (reella) tal som inte kan uttryckas algebraiskt, och kan därav inte definieras som ett nollställe till ett ändligt polynom med rationella koefficienter. Vissa transcendenta tal kan i stället definieras som ett gränsvärde. Talet pi är ett exempel på ett transcendent tal. Motsatsen är algebraiska tal. Däri ingår till exempel alla rationella tal, liksom alla rötter av rationella tal.

Formell definition

Man kan definiera de naturliga talen 0, 1, 2, 3, … genom att först definiera talet noll (0) som den tomma mängden

$0=\varnothing$

och därefter successivt definiera de andra naturliga talen på följande sätt:

• $1=\{0\}\,$

  $2=\{0,1\}\,$

  $3=\{0,1,2\}\,$

  $\vdots \,$

Ett annat sätt att definiera de naturliga talen är att imitera de ryska så kallade matrjosjkadockorna, där det inuti varje docka finns en mindre docka. Till skillnad från den ryska matrjosjkadockan, innehåller den matematiska matrjosjkadockan oändligt många dockor:

• $0=\varnothing \,$

  $1=\{\varnothing \}\,$

  $2=\{\{\varnothing \}\}\,$

  $3=\{\{\{\varnothing \}\}\}\,$

  $\vdots \,$

Bakom de tre punkterna som utgör ellipsissymbolen (…) i uppräkningen av de naturliga talen 0, 1, 2, 3, … ligger den så kallade principen om matematisk induktion; I de två listorna ovan kan man se ett mönster i konstruktionerna av talen 0, 1, 2 och 3. Principen om matematisk induktion låter oss hävda att om vi fortsätter detta mönster i all oändlighet, så har vi lyckats konstruera de naturliga talen.

Informell definition

I meningen "Fem myror är fler än fyra elefanter" är det inte fråga om en jämförelse av storleken hos myror och elefanter, utan det är antalet element i "myrmängden" som är större än antalet element i "elefantmängden". Här är man inte intresserad av att en elefant har mycket större kroppshydda än en myra, även om det kanske är just kroppshyddan som andra först tänker på när de jämför myror med elefanter.

På samma sätt är tusen enkronorsmynt fler än en tusenkronorssedel. Däremot är tusen enkronorsmynt värda lika mycket som en tusenkronorssedel. Här är det en fråga om två olika mått av de två mängderna "Tusen enkronorsmynt" och "en tusenkronorssedel": Det ena måttet (räknemåttet) ger upplysning om antalet element i en mängd, medan det andra måttet (värdemåttet) anger värdet räknat av elementen i en mängd (här i kronor), i den mån det går att mäta mängden med ett sådant mått.

Talrepresentation

Tal kan representeras på fler olika sätt, med olika talsystem.

Markörer

Det unära talsystemet är enklaste sättet att representera tal på. Talen skrivs genom markörer, som streck på en tavla eller papper, eller som stenar. Detta sätt är vanligt för att hålla koll på sportresultat eller föra statistik.

För att beskriva stora tal är det praktiskt att inrätta nya symboler för stora tal. De romerska siffrorna är en variant av detta system.

Räkneord

Ett annat sätt att beskriva tal på är att ge varje tal ett specifikt räkneord. Dessa system är uppdelat i nivåer för att beskriva allt större tal.

Schematiskt sett är räkneorden på svenska uppbyggt på följande sätt: Ett ord för varje tal från 0 till 19, därefter ord för varje 10-tal, antalet hundratal beskrivet från 1 till 9 eller (ännu fler beroende på sammanhang). Nästa nivå är antalet tusental, upp till en miljon. Slutligen ett system som bygger på nivåer - en miljon miljoner är en biljon, en miljon biljoner är en triljon och så vidare. För att uttala ett räkneord börjar man konsekvent med den större nivån och går till den mindre.

Räkneorden och dess uppbyggnad skiljer sig ganska kraftigt åt baserat på språk, även om de flesta språk numera baserar sina räkneord på det decimala talsystemet.

Decimala talsystemet

Det vanligaste sättet att skriva tal på är med det decimala talsystemet, som är ett positionssystem med de tio siffrorna 0, 1, 2, 3, 4, 5, 6, 7, 8 och 9. Det är ett kraftfullt sätt att skriva tal på, och kan varieras på många sätt:

• Med decimaltecken kan det lätt utvidgas att beskriva andra tal än heltal.
• Med minustecken som markör visar den om talet är negativt.
• Med tiopotenser kan man skriva mycket stora och mycket små tal.
• Med hjälp av aritmetiska operatorer kan man beskriva tal med önskvärd precision.
  • Med procent och promille beskrivs hundradelar och tusendelar.
  • Med division kan man beskriva tal i bråk eller i blandad form.
  • Med kvadratrötter och potensuttryck kan man beskriva irrationella tal. Även andra funktioner (som logaritmer och trigonometriska funktioner) och kombinationer av dem kan användas.

Binära talsystemet

Tal representeras med det binära talsystemet i exempelvis datorer. Binära talsystemet är ett positionssystem med de två siffrorna 0 och 1. Med det binära talsystemet kan man representera tal på flera olika sätt. Några olika talrepresentationer:

• Teckenbelopp
• 2-komplement
• Binär offset
• 1-komplement

Vissa representationer har flera sätt att skriva talet 0 på.

Det oktala och hexadecimala talsystemen har sitt ursprung ur binära tal.

Andra talsystem

Det finns även andra talsystem utöver ovanstående, se Lista över talbaser och Kategori:Talsystem.

Historia

Första användningen av tal

Man har hittat ben och andra artefakter med skurna märken, som tros vara räknemärken. Dessa märken kan ha använts för att räkna förfluten tid, till exempel antalet dagar, månens cykler eller bokföring av kvantiteter, till exempel av djur. Ett så enkelt räknesystem har inget positionssystem, vilket gör representation av stora tal klumpigt. Trots detta anses det vara den första typen av ett abstrakt talsystem.

Det första kända talsystem med positionssystem var det mesopotamiska talsystemet med basen 60 (cirka 3400 f.Kr.) och det tidigaste kända positionssystemet med basen 10 uppfanns i Egypten cirka 3100 f.Kr.

Noll

Siffran 0 och därmed positionssystemet sägs ha uppfunnits oberoende av varandra inom tre kulturer, i Mesopotamien, Indien, och Centralamerika.

Först ut verkar den ha använts i Mesopotamien. En nolla kunde där i äldre skrift visas som ett mellanrum i den annars mellanrumsfria kilskriften. I senare kilskrift skrevs nollan mellan två andra siffror med ett tecken bestående av två sneda kilar: . De mesopotamiska matematikerna verkar inte att ha använt någon beteckning för en nolla i början eller slutet av ett tal. Däremot har man funnit trigonometriska tabeller för astronomiskt bruk, med ett tecken för inledande nollor.

Andra symboler för noll konstruerades i mayacivilisationen i nuvarande Guatemala, södra Mexiko och norra Honduras. Mayaindianernas talsystem innehöll dock en oregelbundenhet för att det skulle passa bättre med solåret, varför de inte kunde dra full nytta av uppfinningen. De använde i huvudsak 20 som talbas; men vid räkning av dagar användes även 18, för att på det viset på ett jämnt sätt representera 360 dagar, vilket är ett knappt år. Den efterföljande aztekiska kulturen fortsatte att använda talbasen 20 samt tecken för 0.

Nästa kända uppfinning av nollan var (förmodligen) i Indien. Från 600-talet och framåt har man hittat användning av en punkt eller ibland en liten ring för att beteckna noll. Den äldsta kända daterade inskriptionen med punkt eller cirkel som siffran noll är från Kambodja och gjord år 683. En punkt för noll nämns också i ett 600-talsmanuskript hittat i byn Bakhshali i nordvästra Indien, och i ett kinesiskt astronomiskt verk från 718, som sammanställts av indiska lärda i tjänst hos kejsaren av Kina. Indierna var också de första som räknade med 0 som ett tal. Det är möjligt att den framträdande roll som tomhet hade i indisk filosofi gjorde det naturligare att också uppfatta tecknet för "tom plats" som ett eget tal.

Europa och västvärlden har fått nollan från Indien, även om grekiska astronomer använde en nolla de torde ha "ärvt" från babylonierna i sina trigonometriska tabeller. Kunskapen och användandet av talet noll spreds via den arabiska kulturen till Europa. Noll heter för övrigt "Sifr" på arabiska vilket är ursprunget till ordet "siffra".

Negativa talens historia

Det abstrakta begreppet negativa tal erkändes så tidigt som 100 f.Kr. till 50 f.Kr, först i Kina. Nio Böcker om Räknekonsten (kinesiska: Jiu-zhang Suanshu) innehöll metoder att hitta områdena för siffror, röda slavar användes för att beteckna positiva koefficienter, svarta för negativa. Detta är det tidigaste kända omnämnandet av negativa tal i öst. Det första omnämnandet i väster var på 300-talet i Grekland. Med Diofantos avses ekvationen ekvivalent med 4 x + 20 = 0 (lösningen är negativ) i Arithmetica, som säger att ekvationen gav ett absurt resultat.

Under 600-talet användes negativa tal i Indien för att representera skulder. Diofantos förra hänvisning diskuterades mera explicit med den indiska matematikern Brahmagupta på Brāhmasphuṭasiddhānta år 628, då användes negativa tal för att ge den allmänna formen andragradsekvation som fortfarande används idag.

Europeiska matematiker gjorde, för det mesta, motstånd mot begreppet fram till 1600-talet, även om Fibonaccis negativa lösningar på ekonomiska problem tilläts, där de skulle tolkas som skulder (kapitel 13 i Liber Abaci, 1202) och senare som förluster (i Flos). Samtidigt angav Kina negativa tal genom att rita en diagonal linje genom höger-mest icke-noll-siffra för motsvarande positiva tals siffra. Den första användningen av negativa tal i ett europeiskt arbete var Chuquet under 1400-talet. Han använde dem som exponenter, men kallade dem för "absurda tal".

Så sent som på 1700-talet var det vanligt att ignorera eventuella negativa lösningar till ekvationer på antagandet att de var meningslösa, precis som René Descartes gjorde med negativa lösningar i det kartesiska koordinatsystemet.

Rationella talens historia

Det är troligt att begreppet rationella tal går till förhistorisk tid. De gamla egyptierna använde sin egyptiska bråknotation för rationella tal i matematiska texter såsom Rhindpapyrusen och Kahun-papyrusen. Grekiska och indiska matematiker gjorde studier av teorin om rationella tal, som en del av den allmänna studieplanen i talteori. Den mest kända av dessa är Elementa, cirka 300 f.Kr. Av indiska texter är den mest kända texten Sthananga Sutra, som också omfattar talteori som en del av en allmän studie av matematiken.

Begreppet decimalbråk hänger nära samman med decimal-värdenotation; både verkar ha utvecklats i tandem. Till exempel är det vanligt för Jainism-matematik-sutrorna att inkludera beräkningar av decimalbråksapproximationer till pi eller kvadratroten ur 2. Likaså hade babyloniska matematiska texter alltid använt sexagesimala (bas 60) bråk med stor frekvens.

Irrationella talens historia

Den tidigaste kända användningen av irrationella tal var i den indiska texten Shulba Sutras, cirka mellan 800 och 500 f.Kr. De första existensbevis för irrationella tal brukar tillskrivas Pythagoras, närmare bestämt Pythagoréernas Hippasos av Metapontum, som utarbetade ett (mest sannolika geometriskt) bevis på irrationaliteten i kvadratroten ur 2. Det berättas att Hippasos upptäckte irrationella tal när han försökte representera kvadratroten ur 2 som ett bråk. Men Pythagoras trodde på absolutenessen av tal, och kunde inte acceptera existensen av irrationella tal. Han kunde inte motbevisa dess existens genom logiken, men han kunde inte acceptera irrationella tal, så han dömde Hippasos till döden genom drunkning.

På 1500-talet fördes slutligen europeiskt godkännande av negativa integrerade tal och bråktal. På 1600-talet använde matematiker allmänt decimalbråk med modern notation. Det var dock inte förrän på 1800-talet som matematiker separerade irrationella tal och algebraiska samt transcendenta tal, och ännu en gång genomförde vetenskapliga studier av irrationella tal. Det har varit nästan villande sedan Euklides. År 1872 var publiceringen av teorierna av Karl Weierstrass (och hans elev Kossak), Heine (Crelle, 74), Georg Cantor (Annalen, 5) och Dedekind medfört. År 1869 hade Méray tagit samma utgångspunkt som Heine, men teorin betecknas allmänt som år 1872. Weierstrass metod framgick helt av Salvatore Pincherle (1880), och Dedekind fick ytterligare framträdande genom författarens senaste arbete (1888) och påskrift av Paul Tannery (1894). Weierstrass, Cantor, och Heine baserade sina teorier på oändliga serier, medan Dedekind grundade sin på idén om ett snitt (Schnitt) i systemet med reella tal; separera alla rationella tal i två grupper med karakteristiska egenskaper. Ämnet fick senare tillskott i händerna på Weierstrass, Kronecker (Crelle, 101), och Méray.

Kedjebråk, närbesläktat med irrationella tal (och på grund av Cataldi, 1613), uppmärksammades i händerna på Euler, och som vid sekelskiftet (i början på 1800-talet) fördes in på förgrunden genom skrifter av Joseph Louis Lagrange. Andra anmärkningsvärda bidrag har gjorts av Druckenmüller (1837), Kunze (1857), Lemke (1870), och Günther (1872). Ramus (1855) var först förbunden med föremål med bestämningsfaktorer, vilket, med efterföljande bidrag av Heine, Möbius, och Günther, lade grunden för teorin om Kettenbruchdeterminanten. Dirichlet läggs också till den allmänna teorin, som också har många bidragsgivare till tillämpningarna av ämnet.

Reella talens historia

Under antiken insåg pytagoréerna att längden på hypotenusan för en kvadrat med enhetssida, √2, inte kunde uttryckas som ett rationellt tal (se roten ur två). Detta kom som en överraskning för dåtidens matematiker, som var övertygade om att de rationella talen var fullkomliga. Man insåg att det behövdes fler tal, bland annat för att beskriva kvadratrötter, men även för tal som π. Man lyckades dock inte finna en allmän och precis definition av dessa nya tal.

På 1800-talet revolutionerades denna del av matematiken, då Richard Dedekind gav en enkel men kraftfull konstruktion av de reella talen (se Dedekindsnitt). Han lät ett reellt (positivt) tal representeras av en öppen delmängd ur ℚ₊. Det reella talet är sedan supremum av denna mängd. Om vi låter den aktuella mängden vara M och vi vill skapa decimalutvecklingen r för talet, kan vi gå till väga på detta sätt (för enkelhets skull begränsar vi oss till talen mellan 0 och 1):

1. Vilken är den största tiondel (0,1 0,2 etc.) sådan att det finns tal i M som är större än denna tiondel?
2. Lägg tiondelen till r
3. Vilken är den största hundradel sådan att det finns tal i M som är större än hundradelen + r?
4. Lägg hundradelen till r

Fortsätt oändligt många gånger, med tusendelar, tiotusendelar, etc.

På detta sätt ser vi att ett rationellt tal q representeras i ℝ av mängden {x ∈ ℚ : x<q}. Man visar sedan att de vanliga fyra räknesätten går att definiera för reella tal, och att de ger de resultat vi förväntar oss. Utifrån konstruktionen följer att mängden av de reella talen är fullständig, det vill säga att alla Cauchy-följder har ett gränsvärde (det finns inte några icke-reella tal på tallinjen).

Komplexa talens historia

De komplexa talen har en historia som sträcker sig tillbaka till 1500-talet.

Det förekom kvadratrötter ur negativa tal i de lösningar till tredje- och fjärdegradsekvationer som upptäcktes av de italienska matematikerna Niccolo Fontana Tartaglia och Gerolamo Cardano. Även om man bara var intresserade av reella lösningar, ledde dessa formler ibland till sådana kvadratrötter som mellanresultat.

Namnet imaginära för sådana tal myntades av René Descartes på 1600-talet och man betraktade dem länge med stor misstänksamhet. Komplexa tal accepterades först efter att deras geometriska tolkning hade beskrivits och publicerats av Caspar Wessel 1799. Denna beskrivning återupptäcktes flera år senare av bland andra Carl Friedrich Gauss. Den moderna definitionen som ett par av reella tal infördes under 1800-talet av William Rowan Hamilton.

Flera av Leonhard Eulers mest betydande upptäckter vilar väsentligt på införande av komplexa tal. Abels skapelse, de elliptiska funktionerna, förde än mer de komplexa talen i förgrunden inom matematisk forskning. Så blev ytterligare fallet, när den moderna funktionsteorin framväxte ur Abels, Cauchys, Weierstrass och Riemanns arbeten.

Carl Friedrich Gauss och Karl Weierstrass arbeten har visat, att införande av högre komplexa tal, bildade av flera än två grundenheter, inte medför fördelar jämförliga med dem som vinns genom införande av de av två grundenheter bildade komplexa talen.

Den här artikeln är helt eller delvis baserad på material från Nordisk familjebok, 1904–1926.

Andra begrepp

Siffra

En siffra är ett skrivtecken, en symbol som används för att beteckna tal. I svenska och i andra västerländska språk används de så kallade arabiska siffrorna som egentligen är från Indien. Ordet används ibland även felaktigt som synonym till "tal", särskilt i statistiska sammanhang och liknande: "Nya siffror från opinionsinstitutet A visar att partiet B har förlorat sympatisörer".

Nummer

Ett nummer är en snarlik följd av siffror med en något annorlunda funktion. Där är man inte i första hand är intresserad av matematiska talegenskaper – som till exempel om det är ett primtal – utan av sifferföljdens identifierande funktion. Sifferkombinationen används som ett särskiljande namn och kan i likhet med (andra) namn innehålla olika typer av tecken. IP-nummer/IP-adresser av den sjätte generationen (IPv6) kan skrivas ut både med endast siffror och med en kombination av siffror och bokstäver.

Observera att det engelska ordet number i matematiska sammanhang motsvaras av det svenska ordet tal.

Se även

• Aritmetik
• Kropp
• Linjärt rum
• Lista över tal
• Modul
• Mycket stora tal
• Nummer
• Ring
• Siffra

Referenser

Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Number, tidigare version.

Allmänna källor

• Tobias Dantzig, Number, the language of science; a critical survey written for the cultured non-mathematician, New York, The Macmillan company, 1930.
• Erich Friedman, What's special about this number?
• Steven Galovich, Introduction to Mathematical Structures, Harcourt Brace Javanovich, 23 January 1989, ISBN 0-15-543468-3.
• Paul Halmos, Naive Set Theory, Springer, 1974, ISBN 0-387-90092-6.
• Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972.
• Alfred North Whitehead and Bertrand Russell, Principia Mathematica to *56, Cambridge University Press, 1910.
• George I. Sanchez, Arithmetic in Maya, Austin-Texas, 1961.

Externa länkar

• Wikimedia Commons har media som rör Tal.
  Bilder & media
• Wiktionary har ett uppslag om tal.
  Ordbok
• Wikiversity har kurser eller forskningsmaterial om Tal.
  Kurser
• Om tal filmat på KTH