Thévenins teorem

Thévenins teorem, uppkallat efter den franske telegrafingenjören Léon Charles Thévenin (1857–1926), innebär att varje linjär tvåpol (krets med två anslutningar) bestående av ström- och spänningskällor och resistorer, kan ersättas med en ideal spänningskälla (théveninsk källa) Vth och en seriekopplad resistor Rth.
Den théveninska källan saknar inre resistans och är därmed oberoende av den ström den genererar. Dess duala motsvarighet är den nortonska källan som är en ideal strömkälla, vars ström är oberoende av lasten och har en oändligt hög inre resistans.
- Den ekvivalenta spänningen Vth är den spänning som kan mätas mellan A och B
- Den ekvivalenta resistansen Rth är den resistans som kan mätas mellan A och B om alla ideala spänningskällor ersätts med kortslutningar och alla ideala strömkällor ersätts med ledningsbrott
- Om A och B kopplas samman, är strömmen mellan A och B Vth/Rth (Rth kan beräknas som Vth dividerad med kortslutningsströmmen mellan A och B)
En théveninsk spänningskälla kan ses som en kortslutning, vilket innebär att om kretsen simuleras med en resistans, Rth, i serie med en théveninsk spänningskälla så kan den transformeras till en nortonsk krets med den nortonska strömmen
Teoremet kan även appliceras på ett godtyckligt växelströmsnätverk med linjära källor och med komponenter med reaktiva/komplexvärda impedanser i stället för resistorer.
En oberoende härledning av teoremet gjordes 1853 av den tyske vetenskapsmannen Hermann von Helmholtz.
Exempel[redigera | redigera wikitext]
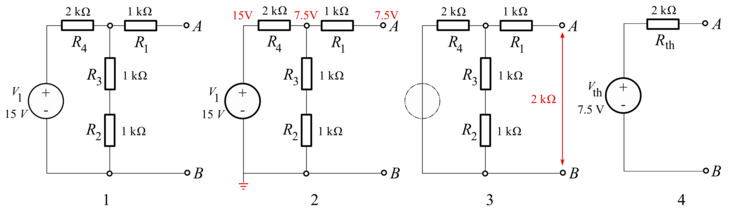
2. Beräkning av den ekvivalenta spänningen
3. Beräkning av den ekvivalenta resistansen
4. Den ekvivalenta kretsen
Beräkning av den ekvivalenta spänningen:
(notera att R1 lämnas obeaktad då beräkningarna är gjorda under förutsättning att kretsen är öppen, att ingen last är ansluten mellan A och B (inget spänningsfall förekommer mellan A och B).
Beräkning av den ekvivalenta resistansen:
Omvandling mellan thevenin/norton-ekvivalenta kretsar[redigera | redigera wikitext]
En norton-ekvivalent krets är relaterad till en thévenin-ekvivalent krets enligt
Se även[redigera | redigera wikitext]
Källor[redigera | redigera wikitext]
- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia.





![{\displaystyle R_{\mathrm {th} }=R_{1}+\left[\left(R_{2}+R_{3}\right)\|R_{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfe26482044ce25efa365f610a3fbd9c0d58dc4e)
![{\displaystyle =1\,\mathrm {k} \Omega +\left[\left(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \right)\|2\,\mathrm {k} \Omega \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88305e6af8f126727745786cc21ac95e058b11e0)



