Reguljär graf
Inom grafteori är en reguljär graf en graf i vilken alla noder har samma grad eller valens. En reguljär riktad graf måste dessutom uppfylla kravet att ingraden är lika med utgraden.[1] En reguljär graf med noder av graden k kallas en k-reguljär graf (eller helt enkelt en reguljär graf av grad k).
De reguljära graferna med en grad upp till och med två är enkla att klassificera. En 0-reguljär graf består av fria noder, en 1-reguljär graf består av fria kanter och en 2-reguljär graf består av fria cykler och oändliga kedjor.
En 3-reguljär graf kallas kubisk graf
En "starkt reguljär graf" är en reguljär graf i vilken alla par av intilliggande noder har samma antal grann-noder gemensamma och varje par av icke intilligande noder har samma antal gemensamma grann-noder. De minsta graferna som är reguljära men inte starkt reguljära är de cykliska och cirkulanta graferna över sex noder. Den kompletta grafen Km är starkt reguljär för alla m.
En sats av Crispin Nash-Williams säger att varje k-reguljär graf över 2k + 1 noder har en Hamiltoncykel.[2]
-
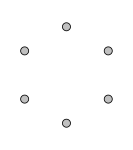
0-reguljär graf
-
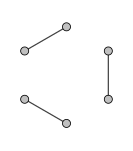
1-reguljär graf
-
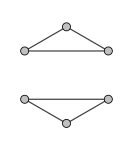
2-reguljär graf
-
3-reguljär graf
Existens[redigera | redigera wikitext]
Det är välkänt att de nödvändiga och tillräckliga förutsättningarna för att en k-reguljär graf av ordning n skall finnas är att n ≥ k + 1 och att produkten nk är jämn. I sådana fall är det lätt att konstruera reguljära grafer genom att beakta lämpliga parametrar för cirkulanta grafer.
Algebraiska egenskaper[redigera | redigera wikitext]
Låt A vara grannmatrisen till en graf. Då är grafen reguljär om och endast om j=(1,1,...,1) är en egenvektor till A.[3] Dess egenvärde är grafens konstanta grad. Egenvektorer som motsvarar andra egenvärden är ortogonala mot j så för sådana egenvektorer v=(v1,...,vn) har vi .
En reguljär graf av grad k är sammanhängande om och endast om egenvärdet k har multipliciteten ett.[3] Det finns också ett villkor för reguljära sammanhängande grafer: En graf är sammanhängande om och endast om ettmatrisen J, med Jij = 1, finns i grafens "sidoalgebra" (det vill säga att den är en linjärkombination av potenser av A)[4]
Låt G vara en k-reguljär graf med diametern D och med grannmatrisens egenvärden . Om G inte är bipartit så
där .[5]
Generation[redigera | redigera wikitext]
Reguljära grafer kan tillverkas med hjälp av programmet GenReg.[6]
Referenser[redigera | redigera wikitext]
- ^ Chen, Wai-Kai (1997). Graph Theory and its Engineering Applications. World Scientific. sid. 29. ISBN 978-981-02-1859-1
- ^ Ashay Dharwadker, Shariefuddin Pirzada, 2011, Graph Theory, ISBN 1466254998, sid. 74.
- ^ [a b] Cvetković, D. M.; Doob, M.; and Sachs, H. Spectra of Graphs: Theory and Applications, 3rd rev. enl. ed. New York: Wiley, 1998.
- ^ Curtin, Brian (2005), ”Algebraic characterizations of graph regularity conditions”, Designs, Codes and Cryptography 34 (2-3): 241–248, doi:.
- ^ [a b] Gregory Quenell, 1992, Spectral diameter estimates for k-regular graphs Arkiverad 6 januari 2014 hämtat från the Wayback Machine., Advances in Mathematics 106, 1994, sid. 122-148.
- ^ Meringer, Markus (1999). ”Fast generation of regular graphs and construction of cages”. Journal of Graph Theory 30 (2): sid. 137–146. doi:. http://www.mathe2.uni-bayreuth.de/markus/pdf/pub/FastGenRegGraphJGT.pdf.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Reguljär graf.
Wikimedia Commons har media som rör Reguljär graf.- Weisstein, Eric W., "Regular Graph", MathWorld. (engelska)
- Weisstein, Eric W., "Strongly Regular Graph", MathWorld. (engelska)
- GenReg, mjukvara och data av Markus Meringer.
- Nash-Williams, Crispin (1969). ”Valency Sequences which force graphs to have Hamiltonian Circuits”. University of Waterloo Research Report. Waterloo, Ontario: University of Waterloo