Traktris
Traktris (från latinets verb trahere "skjuta, dra"; plural: traktriser) är den kurva längs vilken ett objekt rör sig, under inverkan av friktion, då det dras på ett horisontalplan av en lina som är fäst vid en dragande punkt som rör sig vinkelrätt mot utgångslinjen mellan objektet och dragaren med infinitesimal fart. Den är därför en förföljande kurva. Den introducerades första gången av Claude Perrault 1670, och studerades senare av Isaac Newton (1676) och Christiaan Huygens (1692).
Matematisk härledning[redigera | redigera wikitext]
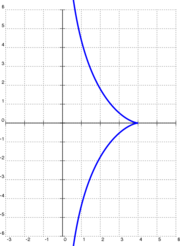
Antag att objektet är placerat vid (a, 0) (eller (4, 0) i exemplet som visas till höger) och att dragaren är placerad i origo, så att a är längden av dragstången (4 i exemplet till höger). Dragaren börjar sedan röra sig längs y-axeln i positiv riktning. Vid varje tidpunkt är dragstången tangent till kurvan y = y(x) som objektet beskriver, och kurvan bestäms helt och hållet av dragarens rörelse. Matematiskt beskrivs rörelsen då av differentialekvationen
med randvillkoret y(a) = 0 vars lösning är
Första termen i denna lösning kan också skrivas
där arsech är den inversa hyperboliska sekantfunktionen.
Den negativa grenen visar fallet när dragaren rör sig i negativ riktning från origo. Båda grenarna hör till traktisen, och möts i en singulär punkt i spetsen (a, 0).
Grunden för traktrisen[redigera | redigera wikitext]
Traktrisens viktigaste egenskap är det konstanta avståndet mellan punkten P på kurvan och skärningspunkten mellan tangenten från P med kurvans asymptot.
Traktrisen kan ses på många olika sätt:
- Det är ortlinjen för centrum av en hyperbolisk spiral som rullar (utan att slira) på en rät linje.
- Involuten till kedjekurvefunktionen, som beskriver en fullt flexibel, oelastisk, homogen sträng fäst vid de två punkterna som utsätts för ett gravitationsfält. Kedjelinjen har ekvationen .
- Banan som bestäms av mitten av bakaxeln på en vagn som dras av ett rep med konstant fart och med konstant riktning (från början vinkelrätt mot fordonets längslinje).
Funktionen tillåter en horisontell asymptot. Kurvan är symmetrisk med avseende på y-axeln. Kurvans radie är
Stor betydelse fick traktrisen genom studiet av rotationsytan av en traktris runt dess asymptot: pseudosfären. Den undersöktes av Beltrami 1868, som en yta med konstant negativ gausskrökning, och är en lokal form av icke-euklidisk geometri.
Idén vidareutvecklades av Kasner och Newman i deras bok Mathematics and the Imagination, där de visar ett leksakståg som drar ett fickur och därvis skapar en traktris.
Egenskaper[redigera | redigera wikitext]

- Tack vare det geometriska sätt som kurvan definieras genom, har traktrisen egenskapen att segmentstycket av dess tangent, mellan asymptoten och tangentens tangeringspunkt, har konstant längd .
- Bågens längd på en gren mellan x = x1 and x = x2 is
- Arean mellan traktrisen och dess asymptot är vilket kan visas genom integration eller med hjälp av Mamikon's theorem.
- enveloppen till traktrisens normal (det vill säga, evoluten till traktrisen) är den kedjekurva som ges av .
- Ytan av en roterande traktris runt dess asymptot är en pseudosfär.
Praktisk användning[redigera | redigera wikitext]
1927, patenterade P.G.A.H. Voigt en hornhögtalare vars konstruktion byggde på antagandet att en vågfront som rör sig genom hornet är sfärisk och har konstant radie. Tanken är att minimera den distorsion som skapas av ljudvågornas reflektioner (studsar) inne i hornet. Den resulterande ytan har formen av en roterande traktriskurva.[1]
Ritmaskiner[redigera | redigera wikitext]
- I oktober–november 1692, beskrev Huygens tre maskiner som kunde rita traktriskurvor.
- 1693 visade Leibniz en maskin som, i teorin, kunde integrera differentialekvationer; maskinens konstruktion använde sig av traktriser.
- 1706 byggde John Perks en traktrismaskin för att lösa hyperbolens kvadratur.
- 1729 byggde Johann Poleni en anordning som byggde på traktriser och möjliggjorde uppritning av logaritmiska matematiska funktioner.
Se även[redigera | redigera wikitext]
- Pseudosfär
- Hyperbolisk funktion för tanh, sech, csch, arccosh
- Naturliga logaritmen för ln
- Signumfunktionen för sgn
- Trigonometrisk funktion för sin, cos, tan, arccot, csc
- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Tractrix, 19 december 2013.
Fotnoter och källor[redigera | redigera wikitext]
Källor[redigera | redigera wikitext]
- Edward Kasner & James Newman (1940) Mathematics and the Imagination, s. 141–143, Simon & Schuster.
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. sid. 5, 199. ISBN 0-486-60288-5
Externa länkar[redigera | redigera wikitext]
- Tractrix on MathWorld
- Module: Leibniz's Pocket Watch ODE at PHASER









