Weibullfördelning
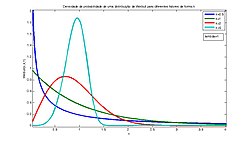
Weibullfördelningen är en kontinuerlig sannolikhetsfördelning inom matematisk statistik.
Den kumulativa fördelningsfunktionen är
Fördelningen är definierad endast för ≥ 0.
- α är en skalningsparameter för x-variabeln
- β är en "skevhetsparameter" eller "formparameter".
- Ibland inför man en tredje parameter genom substitutionen y = x + γ. Den parametern (lägesparametern) frigör funktionen från begynnelsepunkten x = 0 och ger även en ökad flexibilitet vid anpassning av funktionen till experimentella data.
För formparametern kan följande specialfall för täthetsfördelningen nämnas:
- β = 1: täthetsfördelningen är identisk med exponentialfördelningen.[1]
- β = 2 fördelningen är en Rayleighfördelning.[1]
- β < 3: fördelningen är skev åt vänster.[källa behövs]
- β ≈ 3 - 3,5: fördelningen är approximativt symmetrisk och påminner om normalfördelningen.[källa behövs]
- β > 3,5: fördelningen är skev åt höger.[källa behövs]
Weibullfördelningen har stor ingenjörsteknisk användning för studium av livslängd och/eller hållfasthet hos tekniska system, där x är tiden/belastningen, och observerade haverier utgör statistiska observationer av en population tekniska enheter under drift, som exempelvis kullager, vilket var Waloddi Weibulls studieobjekt vid slutet av 1930-talet. Den används ofta för att beskriva keramiska materials variation i hållfasthet.
Om en weibullfördelning anpassas till observerade gångtider till driftstopp hos en komponent kan den funna formparametern indikera fysikaliska samband:
- β = 1: driftstoppen är exponentialfördelade och inträffar slumpmässigt, vilket kan tolkas som att sannolikheten för stopp är oberoende av den ackumulerade gångtiden.
- β < 1: sannolikheten för driftstopp är högst närmaste tiden efter driftsättningen; man talar om inkörningsfel eller "barnsjukdomar".
- β ≈ 3: först efter en viss utslitningstid observeras en större serie (ungefär) normalfördelade driftstopp. Den kunskapen kan utnyttjas för att schemalägga förebyggande underhåll.
Källor[redigera | redigera wikitext]
Vidare läsning[redigera | redigera wikitext]
- Weibull, Waloddi: A statistical theory of the strength of materials, (1939) Ingeniörsvetenskapsakademien Stockholm, rapport 151, ISSN 0368-069X
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Weibullfördelning.
Wikimedia Commons har media som rör Weibullfördelning.
| ||||||||



