Area

Area
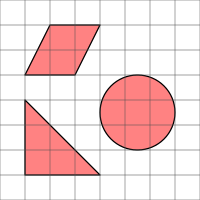Arean av de tre formerna tillsammans är mellan 15 och 16 kvadrater.
Grundläggande
Definition	Utsträckningen av en tvådimensionell yta i planet
Storhetssymbol(er)	$A$ (från latin eller engelska area), $F$, $S$, $Q$
Enheter
SI-enhet	Kvadratmeter (m2)
SI-dimension	L2
CGS-enhet	Kvadratcentimeter (cm2)
CGS-dimension	L2
Planckenhet	Planckarea
Planckdimension	ħ·G·c-3
Astronomisk dimension	L2
Angloamerikansk enhet	acre, sq.in., sq.ft., sq.yd., sq.mi., …
Angloamerikansk dimension	L2

Area är en storhet som beskriver utsträckningen av en tvådimensionell yta i planet. Arean hos en form kan mätas genom att jämföra den med en kvadrat av bestämd storlek. SI-enheten för area är kvadratmeter (m²). Inom matematiken är enhetskvadraten definierad till att ha arean 1. Ibland används yta som synonym till area (men jämför artikeln yta). När man talar om arean hos landområden används ibland areal.

Det finns flera välkända formler som beskriver arean hos enkla geometriska former, såsom trianglar, rektanglar och cirklar. Med dessa formler kan arean av en godtycklig polygon beräknas med polygontriangulering, det vill säga att dela upp polygonen i trianglar. För geometriska former med krökta ränder måste man vanligen använda matematisk analys för att beräkna arean. Faktum är att behovet att kunna bestämma arean hos plana geometriska former var en av anledningarna till att den matematiska analysen utvecklades.

Ytarean hos enkla tredimensionella geometriska former såsom sfärer, koner och cylindrar kunde redan de gamla grekerna bestämma. Mer komplicerade kroppars ytarea kan beräknas med matematisk analys i flera variabler.

Area har stor betydelse inom modern matematik. Detta gäller inte bara den uppenbara betydelsen inom geometri och matematisk analys; area är besläktat med definitionen av determinanter i linjär algebra, och är en grundläggande egenskap i differentialgeometri.

Definition

En ansats att definiera vad som menas med area är genom ett antal axiom. Till exempel kan vi definiera area som en funktion a från en samling speciella plana figurer (benämns mätbara mängder) M till mängden reella tal som har följande egenskaper:

• a(S) ≥ 0 för alla S i M.
• Om S och T tillhör M så gör även S ∪ T, S ∩ T det och a(S ∪ T) = a(S) + a(T) - a(S ∩ T).
• Om S och T tillhör M med S ⊆ T så tillhör T - S också M och a(T - S) = a(T) - a(S).
• Om en mängd S tillhör M och S är kongruent med T så tillhör T också M och a(S) = a(T).
• Varje rektangel R tillhör M. Om rektangeln har längden h och bredden k så är a(R) = hk.
• Låt Q vara en mängd innesluten mellan två rektangelområden S och T. Ett rektangelområde utgörs av en finit union av närliggande rektanglar på en gemensam bas, det vill säga S ⊆ Q ⊆ T. Om det finns ett unikt tal c sådant att a(S) ≤ c ≤ a(T) för alla sådana rektangelområden S och T, så är a(Q) = c.

Enheter

En kvadrat med ytan en kvadratmeter.

Varje längdenhet har en motsvarande ytenhet, där längdenheten motsvarar alla sidor i en kvadrat. Alltså kan area mätas i till exempel kvadratmeter (m²), kvadratcentimeter (cm²), kvadratmillimeter (mm²), kvadratkilometer (km²).

Enhetsomvandlingar

Det går 10 mm på 1 cm, och 100 mm² på 1 cm².

Omvandlingar mellan två ytenheter är kvadraten av deras längdförhållande. Till exempel är

1 cm = 10 mm

och förhållandet mellan cm² och mm² är 100, det vill säga 10².

Vidare är:

• 1 kvadratkilometer = 1 000 000 kvadratmeter
• 1 kvadratmeter = 10 000 kvadratcentimeter = 1 000 000 kvadratmillimeter

Andra enheter

Det finns flera andra vanliga enheter för area. Aret var den första enheten i det metriska måttsystemet, där

• 1 ar = 100 kvadratmeter

Även om ar sällan används idag används hektar fortfarande vanligen som enhet för markarea.

• 1 hektar = 100 ar = 10 000 kvadratmeter = 0,01 kvadratkilometer.

Grundläggande formler för area

Arean hos den här rektangeln är l×w.

Rektanglar

Den enklaste areaformeln är rektangeln. Givet en rektangel med längden l och bredden b, är arean

$A=l\cdot b$   (rektangel)

Alltså, arean hos en rektangel är längden multiplicerat med bredden. Som ett specialfall av detta har en kvadrat med sidolängd s arean

$A=s^{2}$   (kvadrat)

Formeln för arean hos en rektangel följer direkt från de grundläggande egenskaperna hos area, och betraktas ibland som en definition eller ett axiom. Å andra sidan, om geometri utvecklas före aritmetik, kan denna formel användas för att definiera multiplikation av reella tal.

Figurer med samma area.

Dissektionsformeln

De flesta andra enkla formlerna för area följer av dissektion. Detta innebär att man skär en plan figur i bitar, som summerar till arean hos originalfiguren.

Till exempel kan alla parallellogram delas upp i en trapetsoid och en rät triangel (enligt figuren till vänster). Om triangeln flyttas till andra sidan av trapetsoiden resulterar detta i en rektangel. Därför är arena hos en parallellogram samma som för en rektangel:

$A=b\cdot h$   (parallellogram)

Två kongruenta trianglar.

Men samma parallellogram kan också skäras längs sin ena diagonal till två kongruenta trianglar, som i figuren till höger. Från detta får man att arean hos vardera triangel är hälften av arean hos parallellogrammet:

$A={\frac {b\cdot h}{2}}$   (triangel)

Liknande resonemang kan föras för att hitta formler för arean hos trapetsoider, romber och mer avancerade polygoner.

Cirklar

En cirkel kan delas upp i cirkelsektorer, som ungefärligen kan arrangeras som en parallellogram.

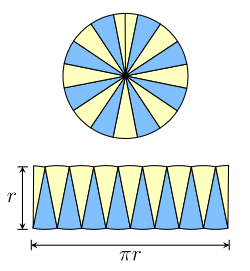
Formeln för cirkelns area grundar sig i en liknande metod. Givet en cirkel med radien r kan den delas in i sektorer enligt figuren till höger. Varje sektor är approximativt en triangulär, och kan fördelas om till en approximativ parallellogram. Höjden hos denna parallellogram är r och bredden hälften av omkretsen hos cirkeln, eller πr. Alltså är den totala arean hos cirkeln r⋅πr eller π⋅r².

$A=\pi r^{2}$   (cirkel)

Trots att dissektionen av cirkeln till sektorer är approximativ blir felet mindre och mindre, ju fler sektorer som cirkeln delas in i. Gränsvärdet som arean hos parallellogrammen går mot är exakt π⋅r², som är cirkelns area. Detta resonemang är en enkel tillämpning av matematisk analys.

Mantelarea

Arkimedes visade att mantelarean och volymen hos en sfär är exakt ⅔ av arean och volymen hos den omkringliggande cylindriska ytan.

De flesta enkla formler för mantelarea kan fås genom att skära upp ytan och släta ut till ett plan. Till exempel, om sidan hos en cylinder eller ett prisma skärs på längden kan ytan slätas ut till en rektangel. På samma sätt, om en kon skärs från basen till toppen kan ytan slätas ut till en cirkelsektor, och arean räknas ut.

Formeln för mantelarean hos en sfär är svårare: eftersom ytan på en sfär har Gausskrökning som är skild från noll kan den inte slätas ut till ett plan. Mantelarean hos en sfär beräknades först av Arkimedes i hans verk 'Om mätning av cirkeln'. Formeln är

$A=4\pi r^{2}$   (sfär)

där r är radien hos sfären. Precis som för cirkeln använder härledningar av denna formel metoder som påminner om matematisk analys.

Lista över areaformler

Vanliga areaformler

Figur	Formel	Variabler
Regelbunden triangel (liksidig triangel)	${\tfrac {1}{4}}{\sqrt {3}}s^{2}$	s är längden hos en sida i triangeln.
Triangel	${\sqrt {s(s-a)(s-b)(s-c)}}$	s är halva perimetern, a, b och c är längderna hos sidorna.
Triangel	${\tfrac {1}{2}}ab\sin(\gamma )$	a och b är två av sidorna, och γ är vinkeln mellan dem.
Triangel	${\tfrac {1}{2}}bh$	b och h är basen och höjden (mätt vinkelrätt basen).
Kvadrat	$s^{2}$	s är längden hos en sida.
Rektangel	$lb$	l och b är längderna hos sidorna (längd och bredd).
Romb	${\tfrac {1}{2}}ab$	a och b är längderna hos de två diagonalerna.
Parallellogram	$bh$	b är ländgden hos basen och h här höjden vinkelrätt mot basen.
Parallelltrapets	${\tfrac {1}{2}}(a+b)h$	a och b är de parallella sidornas längder och h avståndet (höjden) mellan de parallella sidorna.
Regelbunden hexagon	${\tfrac {3}{2}}{\sqrt {3}}s^{2}$	s är längden på en sida hos hexagonen.
Regelbunden oktagon	$2\left(1+{\sqrt {2}}\right)s^{2}$	s är längden på en sida hos oktagonen.
Regelbunden polygon	${\frac {ns^{2}}{4\cdot \tan(\pi /n)}}$	s är längden på sidan, och n antalet sidor.
	${\tfrac {1}{2}}ap$	a är apotemat (radien hos en inskriven cirkel som tangerar polygonen) och p är polygonens omkrets.
Cirkel	$\pi r^{2}$ eller ${\frac {\pi d^{2}}{4}}$	r är radien, och d diametern.
Cirkelsektor	${\tfrac {1}{2}}r^{2}\theta$	r och θ är radien och vinkeln i radianer.
Ellips	$\pi ab$	a och b är halva längden av ellipsens storaxel respektive lillaxel.
Total omslutningsarea (begränsningsarea) hos en Kub	$6s^{2}\,\!$	s är längden av kubens kant.
Total omslutningsarea (begränsningsarea) hos ett Rätblock	$2(ab+ac+bc)\,\!$	a, b och c är längden av rätblockets kanter.
Total omslutningsarea (begränsningsarea) hos en Cylinder	$2\pi r(r+h)\,\!$	$r$ och $h$ är radien och höjden.
Mantelarea hos en cylinder	$2\pi rh$	r och h är radien och höjden.
Total omslutningsarea (begränsningsarea) hos en kon	$\pi r(r+l)$	r och l är radien och längden från basperiferin till toppen.
Mantelarea hos en kon	$\pi rl$	r och l är radien och längden från basperiferin till toppen.
Total ytarea hos en sfär	$4\pi r^{2}\ {\text{or}}\ \pi d^{2}$	r och d är radien och diametern.
Total ytarea hos en regelbunden Pyramid	$B+{\frac {pl}{2}}$	B är basarean, p är basens perimeter och l är apotemat (det vinkelräta avståndet från baspolygonens kanter till toppen).
Konvertering från kvadratisk till cirkulär area	${\frac {4}{\pi }}A$	A är arean hos kvadraten i kvadratisk enhet.
Konvertering från Cirkulär till kvadratisk area	${\tfrac {1}{4}}C\pi$	C är arean hos cirkeln i cirkulär enhet.[förklaring behövs]

Formlerna ovan visar hur arean kan beräknas för många enkla och regelbundna figurer. Arean hos oregelbundna polygoner kan beräknas med koordinatareaformeln.

Se även

• Integraler
• Perimeter
• Volym
• Omkrets
• Areal
• Area och volym för husbyggnader

Referenser

Den här artikeln är helt eller delvis baserad på material från Engelskspråkiga Wikipedia.

Externa länkar

• Wikimedia Commons har media som rör Area.
  Bilder & media
• Wiktionary har ett uppslag om area.
  Ordbok
• Areaformler