Böjtröghetsmoment
- Denna artikel handlar om en kropps motstånd mot böjning. För en kropps motstånd mot rotationsändring, se tröghetsmoment.
Böjtröghetsmomentet för en balk beskriver tvärsnittets förmåga att ta hand om den normalspänning som uppstår när balken böjs. Enligt teknisk balkteori är böjmomentet som erfordras för att erhålla en krökning lika med
där är materialets elasticitetsmodul. Produkten benämns balkens böjstyvhet och är i praktiken ett mått på balkens förmåga att motstå deformation. Böjstyvheten är ej att förväxla med balkens böjmotstånd.
Betrakta en balk orienterad längs x-axeln och med y-axeln riktad uppåt. Koordinatsystemet läggs så att balkens neutrallager återfinns i y = 0. Definitionen av för böjning runt den horisontella z-axeln blir
där integrationen sker över balkens tvärsnitt. För en balk med rektangulärt tvärsnitt med bredden och höjden blir böjtröghetsmomentet runt z-axeln lika med
En rektangulär balk kan ta högre vertikal last om den ställs på högkant jämfört med om den ligger ned.
-
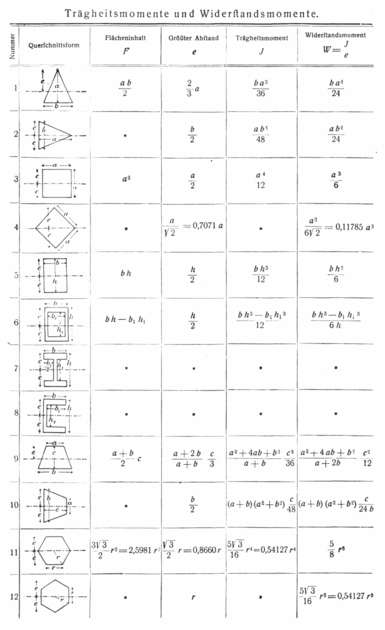
Tabell över böjtröghetsmoment och böjmotstånd
-
Tabell över böjtröghetsmoment och böjmotstånd