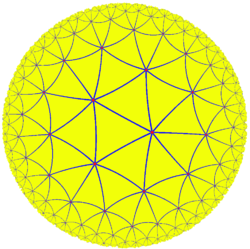
 Hyperboliska trianglar på ett hyperboliskt plan
Hyperboliska trianglar på ett hyperboliskt plan
En hyperbolisk triangel är en triangel på ytan av ett hyperboliskt plan.
En hyperbolisk triangels area är

där

och a, b och c är längderna av triangelns sidor.
Om

är större än noll, så gäller för vinkeln A som är motstående vinkel till sidan med längden a:








