Triangel

För musikinstrumentet, se Triangel (musikinstrument).

Triangeln är en polygon och en av de grundläggande geometriska formerna. En triangel begränsas av tre linjer vars skärningpunkter bildar triangelns hörn.

Triangelns hörn betecknas vanligen med A, B, C och motsvarande vinklar med $\alpha, \beta, \gamma$. Triangeln kan refereras till som triangeln ABC.

Sidan a säges vara motstående sida till hörnet A och vinkeln $\alpha$. Hörnet A sägs vara motstående hörn till sidan a.

Semiperimetern är triangelns halva omkrets eller

$\ s = \frac{1}{2}\left(a+b+c\right)$

Slag av trianglar

En triangel är

• Spetsvinklig om alla vinklar är mindre än 90 grader
• Rätvinklig om en vinkel är rät (90 grader eller $\pi/2$ radianer)
• Trubbvinklig om en av vinklarna är större än 90 grader

• Likbent om två sidor är lika långa
• Liksidig om alla sidor är lika långa

Vinklar

Supplementvinkeln till en vinkel i en triangel kallas yttre vinkel.

Vinkelsumma

En linje som dras genom ett av triangelns hörn och är parallell med motstående sida, visar att triangelns vinkelsumma är 180 grader.

Höjder

En triangels höjder är normaler dragna från en sida, eller en sidas förlängning, till motstående hörn. Höjderna skär varandra i en punkt.

Höjden mot sidan a har längden

$h_a = \frac{2}{a}\sqrt{s(s-a)(s-b)(s-c)}$

där s är semiperimetern. Övriga längder beräknas på motsvarande sätt.

Bisektriser

En bisektris delar en av triangelns vinklar i två lika delar.

Bisektrisen till en yttre vinkel kallas yttre bisektris.

Bisektriserna skär varandra i en punkt som också är den inskrivna cirkelns centrum.

Bisektrisens längd

Längden av bisektrisen från hörnet A är

$v_a = \frac{2 b c \cos \frac{\alpha}{2}}{b + c}$

Bisektrissatsen

En bisektris delar motstående sida i samma proportioner som längderna av de sidor som bildar den delade vinkeln:

$\frac{b}{c} = \frac{x}{y}$

Medianer

Medianen är en linje från ett av triangelns hörn till motstående sidas mittpunkt. Medianerna skär varandra i en punkt.

Medianernas längder är

$m_a = \sqrt {\frac{2 b^2 + 2 c^2 - a^2}{4} }$

$m_b = \sqrt {\frac{2 a^2 + 2 c^2 - b^2}{4} }$

$m_c = \sqrt {\frac{2 a^2 + 2 b^2 - c^2}{4} }$

Area

Triangelns area är en höjd multiplicerad med motsvarande sida dividerat med 2 eller

$A = \frac {a h_a}{2} = \frac {b h_b}{2} = \frac {c h_c}{2}$

Arean kan också beräknas med herons formel som

$A = \sqrt{s(s-a)(s-b)(s-c)}$

där s är semiperimetern (triangelns halva omkrets).

Arean kan även beräknas med den trigonometriska sinusfunktionen enligt

$A = \frac{a b \sin \gamma}{2} = \frac{a c \sin \beta}{2} = \frac{b c \sin \alpha}{2}$

Med integral

Arean av en triangel kan beräknas med integralen

$A = \int_0^h x\frac{a}{h}dx = \left[\frac{a}{2 h} x^2\right] _0^h = \frac{1}{2 h} a h^2 = \frac{1}{2}a h$

Med vektorer

Triangelns area är hälften av arean av en parallellogram med samma bas och höjd

Arean av en parallellogram i ett tredimensionellt euklidiskt rum kan beräknas med hjälp av vektorer. Låt vektorerna AB och AC svara mot sträckan från A till B respektive A till C. Arean av parallellogrammen ABCD är

$|{AB}\times{AC}|,$

vilket är magnituden av kryssprodukten av vektorerna AB och AC. Arean av triangeln ABC är hälften av denna

$\frac{1}{2}|{AB}\times{AC}|$

Triangelns area kan med hjälp av skalärprodukt skrivas som

$\frac{1}{2} \sqrt{(\mathbf{AB} \cdot \mathbf{AB})(\mathbf{AC} \cdot \mathbf{AC}) -(\mathbf{AB} \cdot \mathbf{AC})^2} =\frac{1}{2} \sqrt{ |\mathbf{AB}|^2 |\mathbf{AC}|^2 -(\mathbf{AB} \cdot \mathbf{AC})^2}\,$

I en tvådimensionell euklidisk rymd kan vektorn AB skrivas som (x₁,y₁) och AC som (x₂,y₂), vilket ger arean som

$\frac{1}{2}\,|x_1 y_2 - x_2 y_1|\,$

Samband mellan sidor och vinklar

Cosinussatsen

$a^2=b^2+c^2-2bc\cdot\cos \alpha$

$b^2=a^2+c^2-2ac\cdot\cos \beta$

$c^2=a^2+b^2-2ab\cdot\cos \gamma$

Om till exempel vinkeln $\gamma$ är rät och då $\cos(\pi/2) = 0$ erhålls Pytagoras sats

$c^2\ = a^2 + b^2$

Sinussatsen

$\frac{\sin \alpha}{a}=\frac{\sin \beta}{b}=\frac{\sin \gamma}{c}$

Tangenssatsen

$\frac{a - b}{a + b} = \frac{\tan (\frac{1}{2}(\alpha - \beta))}{\tan (\frac{1}{2}(\alpha + \beta))}$

Cirklar

Omskrivna cirkeln

Den omskrivna cirkelns centrum ligger i skärningspunkten av sidornas mittpunktsnormaler och

dess radie är

$R = \frac{abc}{4\sqrt{s(s-a)(s-b)(s-c)}}$

• 

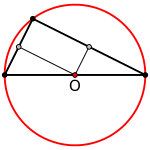
  För en spetsvinklig triangel ligger omskrivna cirkelns mittpunkt inuti triangeln

• 

  För en rätvinklig triangel sammanfaller omskrivna cirkelns mittpunkt med hypotenusans mittpunkt

• 

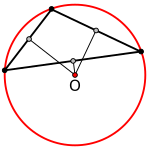
  För en trubbvinklig triangel ligger omskrivna cirkelns mittpunkt utanför triangeln

Inskrivna cirkeln

Den inskrivna cirkelns mittpunkt är bisektrisernas skärningspunkt och dess radie är

$r = \sqrt{\frac{(s-a)(s-b)(s-c)}{s}}$

där s är semiperimetern.

Vidskrivna cirkeln

Bisektrisen från A och bisektrisen från B's yttre vinkel skär varandra i den vidskrivna cirkelns mittpunkt. Den vidskrivna cirkelns radie om cirkeln tangerar sidan a är

$\ r_a = \frac{T}{s - a}$

där T är triangelns area och s semiperimetern.

Kongruensfall

Två trianglar är kongruenta om de kan fås att sammanfalla genom rotation, translation och spegling.

Första kongruensfallet (SVS, sida-vinkel-sida)

Om för ∆ABC och ∆A'B'C' gäller att AB = A'B', AC = A'C' och ∠A = ∠A', så är ∆ABC kongruent med ∆A'B'C'.

Andra kongruensfallet (SSS, sida-sida-sida)

Om för ∆ABC och ∆A'B'C' gäller att AB = A'B', AC = A'C' och BC = B'C', så är ∆ABC kongruent med ∆A'B'C'.

Tredje kongruensfallet (VSV, vinkel-sida-vinkel)

Om för ∆ABC och ∆A'B'C' gäller att AB = A'B', ∠A = ∠A' och ∠B =∠B', så är ∆ABC kongruent med ∆A'B'C'.

Likformighet

Om det för två trianglar med sidorna

$\ a_1, b_1, c_1$ respektive $\ a_2, b_2, c_2$, existerar ett tal $\lambda\,$, en skalfaktor, sådant att

$\ a_1 = \lambda a_2, b_1 = \lambda b_2, c_1 = \lambda c_2$

sägs trianglarna vara likformiga.

Likformighet betecknas

$\triangle ABC \sim \triangle A'B'C'$

Första likformighetsfallet (SVS, Sida-Vinkel-Sida)

Om för två trianglar ABC och A'B'C'

$\frac{|AB|}{|A'B'|} = \frac{|AC|}{|A'C'|}$

och

$\angle A \cong \angle B$

är trianglarna likformiga.

Andra likformighetsfallet (SSS, Sida-Sida-Sida)

Om för två trianglar ABC och A'B'C'

$\frac{|AB|}{|A'B'|} = \frac{|AC|}{|A'C'|} = \frac{|BC|}{|B'C'|}$

är trianglarna likformiga.

Tredje likformighetsfallet (VVV, Vinkel-Vinkel-Vinkel)

Om för två trianglar ABC och A'B'C'

$\angle A \cong \angle A',\quad \angle B \cong \angle B',\quad \angle C \cong \angle C'$

är trianglarna likformiga.

Triangelns tyngdpunkt

En triangelformad ytas masscentrum (tyngdpunkt) ligger på en tredjedel av höjden räknat från basen.

Medianernas skärningspunkt sammanfaller med masscentrum.

Tyngdpunktens avstånd till en sida kan beräknas med en integral. Vi kan anta att ytdensiteten (massa per areaenhet) är = 1. Arean $x\frac{a}{h}dx$ utövar då momentet $x\cdot x\frac{a}{h}dx$ med avseende på origo, vilket för hela triangeln ger

$\int_0^h x\cdot x\frac{a}{h}dx = \left[\frac{a}{3 h} x^3\right] _0^h = \frac{1}{3}a h^2 = \frac{2}{3}A h$

där A är triangelns area. Det moment triangeln utövar kan anses angripa i tyngdpunkten vilket ger

$T_p A = \frac{2}{3}A h\ \rightarrow\ T_p = \frac{2}{3}h \rightarrow d = \frac{h}{3}$

Med lodlina

Det går att finna ett tunt och plant föremåls tyngdpunkt med hjälp av en lodlina. Lodlina och (i detta fall) triangel hängs fritt från en fästpunkt och lodlinjen markeras. Detta upprepas för en andra fästpunkt. Lodlinjernas skärningspunkt är tyngdpunktens läge.

Se även

• Slå upp Triangel i ordlistan Wiktionary.
  Ordbok

• Wikimedia Commons har media som rör Triangel.
  Bilder & media
• Sierpinskitriangel
• Geometri
• Pythagoras sats
• Trigonometri
  • Areasatsen
  • Sinussatsen
  • Cosinussatsen
• Herons formel
• Cirkel
• Hyperbolisk triangel
• Sfärisk triangel