Fil:Relation1101.svg
Utseende

Storleken för denna PNG-förhandsvisning av denna SVG-fil: 384 × 280 pixlar. Andra upplösningar: 320 × 233 pixlar | 640 × 467 pixlar | 1 024 × 747 pixlar | 1 280 × 933 pixlar | 2 560 × 1 867 pixlar.
Originalfil (SVG-fil, standardstorlek: 384 × 280 pixlar, filstorlek: 6 kbyte)
Filhistorik
Klicka på ett datum/klockslag för att se filen som den såg ut då.
| Datum/Tid | Miniatyrbild | Dimensioner | Användare | Kommentar | |
|---|---|---|---|---|---|
| nuvarande | 7 maj 2010 kl. 23.49 |  | 384 × 280 (6 kbyte) | Watchduck | layout change |
| 26 juli 2009 kl. 19.00 |  | 384 × 280 (12 kbyte) | Watchduck | ||
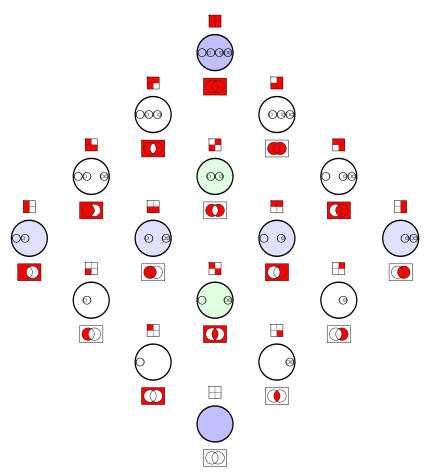
| 10 april 2009 kl. 17.15 |  | 615 × 463 (4 kbyte) | Watchduck | {{Information |Description={{en|1=Venn diagrams of the sixteen 2-ary Boolean '''relations'''. Black (0) marks empty areas (compare empty set). White (1) means, that there ''could'' be something. There are corresponding diagrams of th |
Filanvändning
Inga sidor använder den här filen.
Global filanvändning
Följande andra wikier använder denna fil:
- Användande på de.wikibooks.org