Tryck
- För andra betydelser, se Tryck (olika betydelser).
| Tryck | |
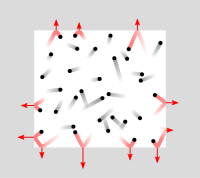 Tryck utövat av gasmolekyler inuti en sluten volym | |
| Grundläggande | |
|---|---|
| Definition | Kraft per areaenhet |
| Storhetssymbol(er) | |
| Härledningar från andra storheter | p = F / A |
| Enheter | |
| SI-enhet | Pa = N/m2 = kg·m-1·s-2 |
| SI-dimension | M·L−1·T−2 |
| CGS-enhet | Bar = dyn/cm2 = cm−1·g·s−2 |
Tryck är kraft per areaenhet som verkar i varje punkt inuti gaser och vätskor och även vinkelrätt mot angränsande fasta kroppars ytor, till exempel kärlets väggar.[1]
Tryck kan definieras som eller
där p är trycket, F är kraften och A areans storlek. SI-enheten för tryck är pascal (1 Pa = 1 newton per kvadratmeter, N/m²).
Då 1 pascal är ett mycket litet tryck används ofta multipelenheter som till exempel hPa, kPa och MPa. Av historiska och praktiska skäl förekommer ytterligare enheter som bar, psi, mmHg, torr, mVp, mmVp, kp/cm2 eller atm.
Mätning och angivelse av tryck[redigera | redigera wikitext]
Tryck kan anges på två olika sätt: som absoluttryck eller tryck relativt omgivningen (över- eller undertryck). Om omgivningen är jordens atmosfär vid havsytan kommer de två sätten att ange tryck att skilja sig med atmosfärstrycket, normalt cirka 1 bar.
Instrument för att mäta tryck mäter ofta trycket relativt omgivande atmosfär, och anger därför tryck som över- eller undertryck relativt omgivande tryck. Påfrestningarna i ett trycksatt system bestäms av tryckskillnaden relativt omgivningen, och anges därför ofta som övertryck.
Egenskaper hos en vätska eller gas (kokpunkt, densitet, entalpi) beror av absoluttrycket, men detta är svårt att mäta då instrumenteringen då behöver ett vakuum som referens. Därför mäts tryck normalt i övertryck, men räknas om till absoluttryck vid termodynamiska analyser.
Om exempelvis omgivningens tryck på mätinstrumentets referenssida uppgår till 1 bar,a (absoluttryck), och trycket till exempel inuti en tryckluftstank uppgår till 10 bar,a så kommer instrumentet som mäter tryckluftstankens tryck att visa 9 bar,ö (svensk notation, internationellt används såväl är bar,e som bar,g).
Instrument för mätning av tryck är barometer och manometer.
Lufttryck[redigera | redigera wikitext]
Lufttrycket är det tryck atmosfären åstadkommer och lufttrycket avtar ungefär exponentiellt med höjden. Försök har gjorts att bestämma ett medelvärde för lufttrycket vid havsytan i olika standarder, exempelvis STP och NTP. I dessa standarder anges det normala lufttrycket vid havsytan som 1 atm, det vill säga 101,325 kPa.

Som modeller för att beräkna trycket i atmosfären under 86 km finns två ekvationer som bygger på fördefinierade parametrar. Den första ekvationen används när den hastighet med vilken atmosfärens temperatur ändras med ökningen av höjden (en. lapse rate) är skild från noll och den andra ekvationen används då denna hastighet är noll. Ekvationen då hastigheten är nollskild
och då hastigheten är noll
där indexet b varierar från 0 till 6 och betecknar de sju lägsta lagren i atmosfären vilkas höjder är 0, 11, 20, 32, 47, 51 och 71 kilometer och där
- = statiska trycket (pascal)
- = standardtemperaturen (K), den antagna temperaturen som funktion av luftlagrets höjd
- = standardtemperaturens lapse rate (K/m) i ISA
- = höjd över havet (meter)
- = höjden för understa delen av luftlagret b (meter)
- = gaskonstanten för luft: 8.31432 N·m /(mol·K)
- = den antagna tyngdaccelerationen (9.80665 m/s2)
- = massan per mol för jordens atmosfär (0.0289644 kg/mol)
Hydrostatiskt tryck[redigera | redigera wikitext]

Med det hydrostatiska trycket avses det tryck som en vätska (vanligtvis vatten) orsakar.
Under vattenytan ökar trycket med en bar (cirka 100 kPa) för var tionde meter.
Det totala trycket som råder i en bestämd punkt på jorden är summan av lufttrycket och det eventuella hydrostatiska trycket.
Antag en vattenpelare, som sträcker sig från en vattenyta och ned till ett djup h. Vattenpelaren åstadkommer ett tryck på sin bottenarea A som är
där Ph är det hydrostatiska trycket, m är vattnets massa och g tyngdaccelerationen. En kropps massa kan skrivas som
där ρ är densiteten och V är volymen, vilket ger
Det totala trycket vid ett bestämt djup ges då av
där P0 är lufttrycket.
Hydrodynamiskt tryck[redigera | redigera wikitext]
Med det hydrodynamiska trycket avses den rörelseenergi per volymenhet som vatten och andra inkompressibla fluider har vid strömningar i rör och kanaler.
Den klassiska formen för rörelseenergi E brukar skrivas
Genom att dividera fluidens totala rörelseenergi E med dess volym V, erhålls det hydrodynamiska trycket Pd enligt
och SI-enheten för det hydrodynamiska trycket blir Pascal.
För en ideal inkompressibel fluid som passerar genom en plan sektionsförändring, blir summan av det hydrostatiska och hydrodynamiska trycket konstant, det vill säga
där Ph är hydrostatiskt tryck och Pd är hydrodynamiskt tryck. I verkligheten sker alltid en tilläggsförlust (ht) vid alla sektionsförändringar, varför uttrycket då skrivs
Trycket för en ideal gas[redigera | redigera wikitext]
För en ideal gas, antas att molekylerna saknar volym och att den enda växelverkan som förekommer är elastiska kollisioner med andra gasmolekyler eller med eventuella kärlväggar som innesluter gasen. Trycket antas variera linjärt med temperatur, volym och mängd i enlighet med den ideala gaslagen
där
- p: gasens absoluta tryck
- n: substansmängden (ämnesmängden)
- T: den absoluta temperaturen
- V: volymen
- R: allmänna gaskonstanten
En verklig gas uppvisar ett mer komplext beroende av gasens tillståndsparametrar. [2]
Samband mellan enheter för tryck[redigera | redigera wikitext]
| Omvandlingstabell för tryckenheter | |||||||
|---|---|---|---|---|---|---|---|
| Pascal | bar (a) | Atmosfär | Teknisk atmosfär | Torr | Skålpunds-kraft per kvadrattum |
cm vattenpelare | |
| [Pa] | [bar] | [atm] | [at] | [Torr]≈[mmHg] | [psi] | [cmH2O] | |
| 1 Pa | ≡ 1 N/m2 | 10−5 | 9,8692×10−6 | 1,0197×10−5 | 7,5006×10−3 | 145,04×10−6 | 0,0101972 |
| 1 bar (a) | 100 000 | ≡ 106 dyn/cm2 | 0,98692 | 1,0197 | 750,06 | 14,5037744 | 1019,72 |
| 1 atm | 101 325 | 1,01325 | ≡ 1 atm | 1,0332 | 760 | 14,696 | 1033,23 |
| 1 at | 98 066,5 | 0,980665 | 0,96784 | ≡ 1 kgf/cm2 | 735,56 | 14,223 | 1000,02 |
| 1 Torr | 133,322 | 1,3332×10−3 | 1,3158×10−3 | 1,3595×10−3 | ≡ 1 Torr; ≈ 1 mmHg | 19,337×10−3 | 1,35951 |
| 1 psi | 6,894×103 | 68,948×10−3 | 68,046×10−3 | 70,307×10−3 | 51,715 | ≡ 1 lbf/tum2 | 70,3072 |
| 1 cmH2O | 98,0665 | 0,980665×10−3 | 0,967838×10−3 | 9,99984×10−4 | 0,73556 | 0,0142233 | ≡ 1 cmH2O |
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Norstedts uppslagsbok 1948
- ^ P. Atkins, J. de Paula Elements of Physical Chemistry, 4th Ed, W.H. Freeman, 2006. ISBN 0-7167-7329-5.




![{\displaystyle {P}=P_{b}\cdot \left[{\frac {T_{b}}{T_{b}+L_{b}\cdot (h-h_{b})}}\right]^{\textstyle {\frac {g_{0}\cdot M}{R^{*}\cdot L_{b}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e363f986334fd93291552eadd3e9a100b7ce2d45)
![{\displaystyle P=P_{b}\cdot \exp \left[{\frac {-g_{0}\cdot M\cdot (h-h_{b})}{R^{*}\cdot T_{b}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fba1b5af4f6ebe93e2c4e2e78cca45efb6f69d4)
















