Andragradsyta

Inom matematiken är en andragradsyta en D-dimensionell hyperyta definierad som lösningsmängden till ett kvadratiskt polynom. Med koordinater {x₀, x₁, x₂, …, x_D} definieras den allmänna andragradsytan av ekvationen

$\sum _{i,j=0}^{D}Q_{i,j}x_{i}x_{j}+\sum _{i=0}^{D}P_{i}x_{i}+R=0$

där Q är en D+1 dimensionell matris, P är en D + 1 dimensionell vektor, och R en konstant. Värdena Q, P och R tas ofta som reella tal eller komplexa tal.

I normalform skrivs en tre-dimensionell (D = 3) andragradsyta centrerad i origo (0,0,0) som:

${\frac {x^{2}}{a^{2}}}\pm {\frac {y^{2}}{b^{2}}}\pm {\frac {z^{2}}{c^{2}}}=1$

Med translationer och rotationer kan varje andragradsyta transformeras till en av flera normalformer. I det tredimensionella euklidiska rummet finns 16 sådana normalformer och de mest intressanta är

Yta	Ekvation	Plot
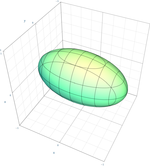
Ellipsoid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,$
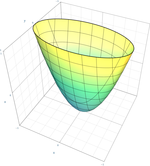
Elliptisk paraboloid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,$
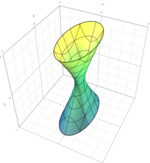
Hyperbolisk paraboloid	${x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,$
Enmantlad elliptisk hyperboloid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,$
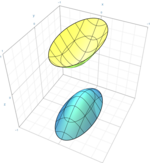
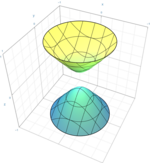
Tvåmantlad elliptisk hyperboloid	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1$
Elliptisk cylinder	${x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,$
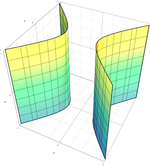
Hyperbolisk cylinder	${x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,$
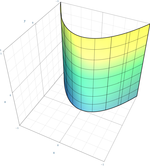
Parabolisk cylinder	$x^{2}+2ay=0\,$
Sfäroider (specialfall av ellipsoider)	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,$
Sfär (specialfall av sfäroid)	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}=1\,$
Cirkulär paraboloid (specialfall av elliptisk paraboloid)	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,$
Enmantlad cirkulär hyperboloid	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=1$
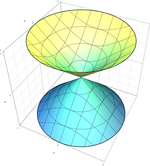
Tvåmantlad cirkulär hyperboloid	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=-1$
Elliptisk kon	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over b^{2}}=0$
Cirkulär cylinder	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1$
Cirkulär kon	${x^{2} \over a^{2}}+{y^{2} \over a^{2}}=0$

Se även

• Kvadratisk form

Externa länkar

• [1], Quadrics in Geometry Formulas and Facts av Silvio Levy, utdrag från 30:e upplagan av "CRC Standard Mathematical Tables and Formulas (CRC Press)".

Matematikportalen – portalen för matematik på svenskspråkiga Wikipedia.