Cyklisk grupp

Inom matematiken är en cyklisk grupp en grupp som kan genereras av ett enskilt element, dvs att gruppen har ett element a (som kallas gruppens generator) sådant att varje element i gruppen är en potens av a och ekivalent att ett element a i en grupp G genererar G exakt om den enda delgruppen i G som innehåller a även är G.

Klassifikation

De cykliska grupperna är de enklaste grupperna och de är fullständigt klassificerade: för varje positivt heltal n finns en cyklisk grupp C_n av ordning n, därutöver finns den oändliga cykliska gruppen, tilläggsgruppen vars element utgörs av heltalen Z. Varje cyklisk grupp är isomorf med en av dessa grupper.

Exempel

Alla lösningar till $w^6 = 1$ bildar en grupp under multiplikation.

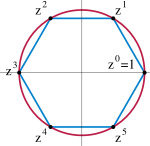
Mängden av heltal modulo n $\Z_n = \{0,2,\ldots, n-1\}$ med gruppoperationen addition modulo n bildar en cyklisk grupp med generator 1 (för alla n>1 finns åtminstone en till generator (n-1)).

Egenskaper

En cyklisk grupp är alltid kommutativ, eftersom $a^m a^n = a^{m+n} = a^{n+m} = a^n a^m$ . Cykliska grupper är alltså abelska grupper. Abelska grupper är moduler över ringen Z av heltal, och en abelsk grupp är cyklisk som grupp precis om den är en cyklisk Z-modul.

Varje delgrupp i en cyklisk grupp är cyklisk.

Om a genererar en cyklisk grupp G av ordning n så får elementet $a^k$ ordningen:

$o(a^k) = \frac{n}{\operatorname{SGD}(n,k)}$

där $\operatorname{SGD}(n,k)$ är största gemensamma delare. Så att elementet $a^k$ är en generator till G om och endast k och n är relativt prima.

För cykliska grupper gäller även omvändningen till Lagranges sats, dvs om G är en grupp av ordning n och $k>0$ delar n så finns en undergrupp i G som har ordning k.