Dubbelpendel
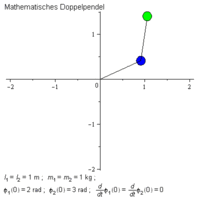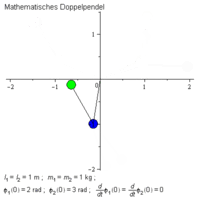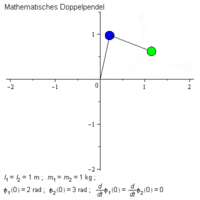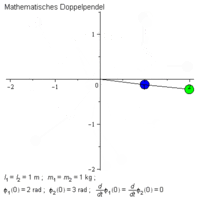
, g = gravitationskonstanten). Där den svänger 10 gånger under tiden är markerat med grönt (= 10 ), 100 gånger med rött, 1000 gånger med lila, och 10000 med blått.En dubbelpendel är en modell över en naturlig process när två sammankopplade pendlar samtidigt rör sig. På den ena pendeln hängs en längre pendel. Modellen är ett sätt att beskriva en kaotisk process (kaosteori). Pendlarna tenderar att röra sig i cirklar på grund av tyngdkraften och störande moment (se skissen längst till vänster nedan och bilden bredvid).
Denna enkla konstruktion kan nämligen visa på ett oförutsebart rörelsemönster, som reagerar exponentiellt (se om exponenter i artikeln potens (matematik)) på störningar av den, det vill säga reagera dubbelt eller mångdubbelt på en tillförd störning (exponenten påverkas matematiskt).
Förhållandena följer av icke-linjär dynamik, som innebär elliptiska och hyperboliska fixpunkter.
Synbarligen är i bestämda tillstånd (fasrumpositioner) en liten ändring utslagsgivande för den omedelbara utvecklingen därefter.
Exempel: För en penna, som står på sin spets, räcker det med en ytterst liten oregelbundenhet ur pennans lodräta linje, för att den ska falla i en bestämd riktning.
[redigera] Bilder och skisser
-
Översikt över de beräknade krafterna hos en dubbelpendel
-
En dubbelpendels rörelser fotograferat med en sekunds slutarhastighet
-
Översikt över de mönster en dubbelpendel gör
[redigera] Se även
[redigera] Externa länkar
- Dubbelpendel på Java (på engelska)
- Härledning (på engelska) av differentialekvationer för att beskriva en dubbelpendel
- Denna artikel är helt eller delvis baserad på material från tyskspråkiga Wikipedia
- Artikeln är, helt eller delvis, en översättning från engelskskspråkiga Wikipedia.
