Henons attraktor

Henons attraktor är ett exempel på ett diskret dynamiskt system. Den har fått sitt namn efter den franska astronomen och matematikern Michele Henon. Då den ursprungliga attraktorn som lades fram av Henon uppvisar kaotiska egenskaper gör det Henons attraktor till ett av de mest kända exemplen på ett dynamiskt system med kaotiskt beteende.
Historia[redigera | redigera wikitext]
Michele Henon arbetade under 1960- och 70-talen med att studera dynamiken bakom hur stjärnor och andra himlakroppar förflyttar sig inuti galaxer. Henon upptäckte attraktorn när han försökte skapa en modell för dessa himlakroppars kaotiska banor då de påverkas av en gravitationskälla.
Hur man skapar Henons attraktor[redigera | redigera wikitext]
Henons attraktor är en fraktal som tillhör gruppen kaotiska attraktorer. En kaotisk attraktor är det underliggande mönster som uppkommer då ett kaotiskt system plottas i en graf.
För att skapa Henons attraktor behöver man ett ekvationssystem med två ekvationer, en ekvation för x-värden och en ekvation för y-värden, och en startpunkt (xn,yn). Den första attraktorn som skapades av Michele Henon på 1970-talet använde sig av följande två ekvationer:
Ekvationssystemet appliceras på startpunkten varvid en ny punkt uppkommer. Denna punkt plottas i en graf och processen upprepas på nytt med denna nya punkt. Fortsätter man denna iteration och räknar ut nya värden som plottas i grafen (väldigt många värden) så kommer ett mönster att börja framträda. Detta mönster är Henons attraktor.
Egenskaper[redigera | redigera wikitext]
Till en början kommer denna process att till synes placera punkter helt slumpmässigt i grafen. Först när ett stort antal värden har plottats kommer ett mönster att framträda. Fortsätter iterationen så kommer punkterna snart att bli så många att de ser ut att bilda heldragna linjer. Om man vid det laget zoomar in på de linjer som har bildats, kommer man snart märka att det som från början såg ut som enskilda linjer i själva verket är uppbyggda av andra linjer. Denna egenskap, att det är möjligt att zooma in och få en likadan bild igen, kallas "self-similarity" och är en egenskap som finns hos många fraktaler. Egenskapen förutsätter att ett oändligt antal iterationer genomförs, annars kommer man för eller senare se hur linjerna successivt löses upp i enskilda punkter.
-
Ursprungliga Henons attraktor
-
8X förstoring av Henons attraktor
-
64X förstoring av Henons attraktor
-
512X förstoring av Henons attraktor
Parametrarna a och b[redigera | redigera wikitext]
Som man ser i ekvationen ovan beror formlerna på två parametrar, a och b. Parametrarna a och b bestämmer hur värdena som fås då ekvationssystemet appliceras på en punkt kommer att bete sig, det vill säga om systemet till exempel kommer att bete sig kaotiskt eller oregelbundet. För den första attraktorn använde sig Henon av värdena och vilka skapar attraktorn i bilden högst upp.
Det är möjligt att ändra på värdena för a och b och på så sätt skapa attraktorer som skiljer sig från den på bilden. Det gäller dock att vara försiktig, då det endast är möjligt att göra små förändringar i ett litet intervall kring originalvärdena för a och b om fraktalen fortfarande ska likna Henons attraktor.
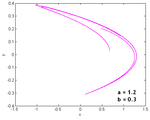
Här nedan finns några bilder på andra Henons attraktorer med olika värden för a och b.
-
a=1.2 b=0.3
-
a=1.3 b=0.3
-
a=1.4 b=0.3
-
a=1.4 b=0.1
-
a=1.5 b=0.2
Referenser[redigera | redigera wikitext]
- http://mathforum.org/mathimages/index.php/Henon_Attractor
- http://en.wikipedia.org/wiki/Henon_map
- http://brain.cc.kogakuin.ac.jp/~kanamaru/Chaos/e/Henon/
- http://www.bookrags.com/tandf/hnon-map-tf/[död länk]
- https://web.archive.org/web/20081010165746/http://library.thinkquest.org/3703/pages/henon.html