Komplexkonjugat
Utseende
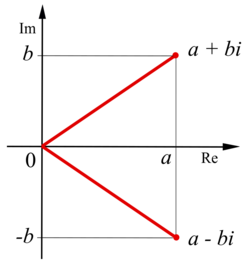
Komplexkonjugatet till ett komplext tal är det komplexa tal som har samma realdel och där imaginärdelen har samma belopp men är av motsatt tecken[1]. Konjugering innebär att i det komplexa talplanet avbilda talet som dess spegling i den reella axeln. Komplexkonjugatet av ett tal betecknas med eller och kan definieras som
Till exempel är
Egenskaper[redigera | redigera wikitext]
För alla komplexa tal och gäller
- om
- om och endast om är reellt
- om
Komplexkonjugering är ett av de enklaste exemplen på en icke-analytisk funktion.
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Weisstein, Eric W. "Complex Conjugate." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ComplexConjugate.html
| |||||




















