Sinc-funktionen
Sinc-funktionen är en av två möjliga matematiska funktioner som vanligtvis betecknas sinc(x).
-
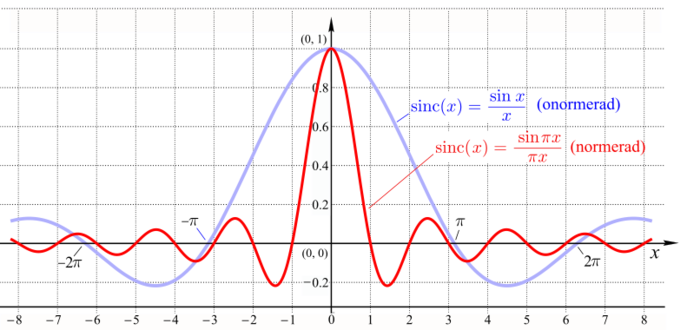
Den onormaliserade (blå) och normaliserade (röd) sinc-funktionen
Inom teorin för signalbehandling och relaterade områden definieras oftast sinc-funktionen som
vilket är den normaliserade sinc-funktionen. Inom matematiken används den onormaliserade sinc-funktionen
För båda definitionerna, är värdet vid x = 0 definierat som gränsvärdet
för alla reella a ≠ 0.
Egenskaper[redigera | redigera wikitext]
Den normaliserade sinc-funktionen har nollställen vid alla heltal utom noll (den onormaliserade har nollställen för alla ). Den kan också representeras som en produkt enligt
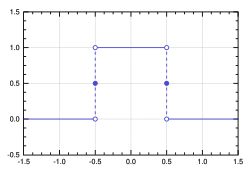
Fouriertransformen av den normaliserade sinc-funktionen är rektangelfunktionen rect(f),
där rect(f) = 1 då f ligger i intervallet {−1/2, 1/2} och noll för övriga värden.