Corioliseffekten
Corioliseffekten är förändringen av ett rörligt objekts rörelseriktning, som kan observeras, när objektet betraktas i ett roterande referenssystem.[1] Fenomenet har fått sitt namn efter fransmannen Gaspard-Gustave Coriolis, som 1835 beskrev det i samband med teorin om vattenhjul. Den fiktiva kraft som associeras med effekten kallas corioliskraft. I början av 1920-talet började termen corioliskraft att användas inom meteorologin, för att förklara luftmassors rörelser över jordytan.
Jordens rotation orsakar corioliseffekter och dessa har en stor inverkan på klimatet. Corioliskraften påverkar stora luftmassor och kan få stormar och orkaner att rotera. Den ger också upphov till så kallade uppvällningar, vilka ligger till grund för den höga halten av biomassa i hav utmed västkuster. Corioliskraften har ett avgörande inflytande på strömningar i atmosfären och haven genom sin tendens att överföra horisontella rörelser till cirkelrörelser.
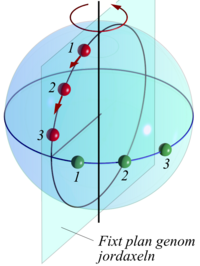
Ett exempel på corioliseffekt visas i bilden till höger. Ett föremål förflyttar sig söderut i ett icke-roterande plan genom jordens rotationsaxel. En observatör som befinner sig på en fast punkt på jordens yta öster om föremålet, roterar med jorden vidare österut och uppfattar därför att föremålet böjer av i västlig riktning.
Översikt[redigera | redigera wikitext]

Övergång till ett roterande referenssystem leder till ändringar av rörliga objekts riktningar så som de uppfattas i det roterande systemet. I ett referenssystem med medurs rotation, är avvikelsen till vänster om rörelseriktningen, i ett med moturs rotation, sker avvikelsen åt höger.[1]
Newtons rörelselagar beskriver rörelsen av ett objekt i ett (icke-accelererande) inertialsystem. När Newtons lagar transformeras till ett likformigt roterande referenssystem, uppträder coriolis- och centrifugalkrafter. Båda krafterna är proportionella mot objektets massa. Corioliskraften är proportionell mot rotationshastigheten och centrifugalkraften är proportionell mot dess kvadrat. Corioliskraften verkar i en riktning vinkelrät både mot det roterande referenssystemets rotationsaxel och mot kroppens hastighetsriktning i det roterande systemet och dess storlek är proportionell mot objektets hastighet i det roterande systemet. Centrifugalkraften verkar utåt i radiell riktning och är proportionell mot kroppens avstånd till axeln i det roterande systemet.[2] Dessa ytterligare krafter kallas tröghetskrafter, fiktiva krafter eller pseudokrafter. De tillåter tillämpning av Newtons lagar i ett roterande system. De är korrigeringsfaktorer som inte existerar i ett icke-accelererande system.[3]
Fysikaliska mätningar görs vanligen med hänsyn till ett koordinatsystem, som är fixerat till jorden, vilket därför roterar med en konstant vinkelhastighet i förhållande till ett inertialsystem. Corioliseffekten orsakas av jordens rotation och trögheten hos den massa som påverkas. Eftersom jorden bara fullbordar ett varv per dygn, är corioliskraften relativt liten och dess effekter blir allmänt märkbara endast för rörelser över stora avstånd och under relativt långa tidsperioder, såsom storskalig förflyttning av luft i atmosfären eller vatten i havet. Sådana rörelser begränsas av jordytan, så att endast den horisontella komponenten av corioliskraften är generellt viktig.
Denna kraft orsakar att rörliga objekt på norra halvklotet böjs av i medurs riktning i förhållande till färdriktningen och på södra halvklotet i moturs riktning. Hellre än att flöda direkt från områden med högt tryck till områden med lågt tryck, som de skulle i ett icke-roterande system, tenderar vind och strömmar att böja av till höger om denna riktning norr om ekvatorn och till vänster om denna riktning söder om ekvatorn. Denna effekt är ansvarig för stora cykloners rotation.[4]
Illustration av corioliseffekten[redigera | redigera wikitext]

Vänster: Sedd från ett inertialsystem
Höger: Sedd från den roterande ramen
Corioliseffekten kan demonstreras med en grund, roterande parabolisk skål. På en plan yta, skulle trögheten hos ett medroterande objekt tvinga det utanför kanten. Om emellertid den paraboliska skålen roteras med en till skålen anpassad hastighet, blir den horisontella normalkraftskomponenten lika med den centripetalkraft som är nödvändig för att hålla det friktionsfria objektet kvar i skålen. Ovanstående experiment tillåter att corioliseffekten visas i frånvaro av andra krafter.
Skivor skurna från cylindrar av torris kan användas som puckar, som nästan friktionsfritt kan flyttas runt på den paraboliska skålens yta, vilket gör att corioliseffekterna visar sig i form av dynamiska fenomen. I den vänstra panelen till höger, som visar vad som ses av en stationär observatör, kommer tyngdkraften att dra objektet mot mitten av skålen med en kraft som är proportionell mot föremålets avstånd till centrum. Tillsammans med centripetalkraften uppstår en elliptisk rörelse.
I den högra panelen, som visar hur förloppets ses i den roterbara ramen, är den inåtriktade normalkraftskomponenten balanserad av den utåtriktade centrifugalkraften (närvarande endast i den roterande ramen). Med dessa två krafter balanserade är den enda obalanserade kraften corioliskraften (närvarande endast i den roterande ramen) och rörelsen är en cirkelrörelse, då corioliskraften är vinkelrät mot objektets rörelseriktning.
Analys och observation av cirkulär rörelse i den roterande ramen är enklare jämfört med analys eller observation av elliptisk rörelse i inertialramen.
Eftersom referensramen i detta fall roterar flera gånger per minut i stället för bara en gång per dygn som jorden, är coriolisaccelerationen här många gånger större och därmed lättare att observera under laboratorieförhållanden jämfört med den coriolisacceleration som orsakas av jordens rotation.
Meteorologi[redigera | redigera wikitext]



Den kanske viktigaste manifestationen av corioliseffekten är den storskaliga dynamiken i haven och atmosfären. Inom meteorologi och oceanografi, är det lämpligt att postulera en roterande referensram där jorden står stilla. Som en konsekvens av det valet introduceras centrifugalkrafter och corioliskrafter. Deras relativa betydelse bestäms av tillämpliga rossbytal. Tornador har höga rossbytal och medan tornadoassocierade centrifugalkrafter är ganska betydande, är corioliskrafter förknippade med tornados praktiskt taget försumbara.[5]
Luften inuti högtryckssystem roterar i en sådan riktning att corioliskraften riktas radiellt inåt och nästan balanseras av den utåt radiellt riktade tryckgradienten. Som ett resultat, färdas luften medurs runt högtryck på norra halvklotet och moturs på södra halvklotet. Luft inuti lågtryckssystem roterar i motsatt riktning, så att corioliskraften är riktad radiellt utåt och nästan balanserar en inåt radiellt riktad tryckgradient.
Flöde runt ett lågtrycksområde[redigera | redigera wikitext]
Om ett lågtrycksområde formas i atmosfären, kommer luft att tendera att strömma i riktning mot området, men kommer att böjas av vinkelrätt mot dess hastighet genom corioliskraften. Ett system i jämvikt kan då etablera sig och skapar en cirkulär rörelse, eller ett cyklonflöde. Eftersom rossbytalet är lågt, är det i stort sett kraftbalans mellan tryckgradientens kraft som verkar i riktning mot lågtrycksområdet och corioliskraften som verkar i riktning bort från centrum av lågtrycket.
I stället för att flöda i tryckgradientens riktning, tenderar storskaliga rörelser i atmosfären och haven att förekomma vinkelrätt mot tryckgradienten. Detta kallas geostrofiskt flöde.[6] På en icke-roterande planet, skulle en fluid flöda längs den rätast möjliga linjen och snabbt eliminera tryckgradienter. Observera att geostrofisk balans är mycket annorlunda än fallet med "tröga rörelser" (se nedan), vilket förklarar varför cykloner på mellanbreddgrader är en storleksordning större än vad en tröghetscirkels flöde skulle vara.
Detta mönster av avvikelser och rörelseriktningar, kallas Buys-Ballots lag. I atmosfären kallas flödets mönster en cyklon. På norra halvklotet är rörelseriktningen runt ett lågtrycksområde moturs. På södra halvklotet är rörelseriktningen medurs eftersom rotationsdynamiken där är en spegelbild. På höga höjder, roterar luft som sprids utåt i motsatt riktning.[7] Cykloner bildas sällan längs ekvatorn beroende på den svaga corioliseffekten i denna region.
Tröghetscirklar[redigera | redigera wikitext]

En luft- eller vattenmassa som rör sig med hastigheten och endast är föremål för corioliskraften, färdas i en cirkulär bana som kallas tröghetscirkel. Eftersom corioliskraften är riktad vinkelrätt mot massans rörelseriktning, kommer den att röra sig med en konstant hastighet i en cirkel med radien enligt
där är coriolisparametern (där är latituden). Den tid det tar för massan att fullborda en cirkel är därför . Coriolisparametern har ett typiskt värde för mellanliggande latituder av omkring 10−4 s−1. För en typisk atmosfärisk hastighet av 10 m/s är då radien 100 km och med en period på omkring 17 timmar. För en ström i en ocean med en typisk hastighet av 10 cm/s, är en tröghetscirkels radie 1 km. Dessa tröghetscirklar roterar medurs på den norra hemisfären och moturs på den södra hemisfären.
Myt[redigera | redigera wikitext]
Ett vanligt förekommande påstående är att corioliseffekten får utrinnande vatten i badkar och handfat att rotera och att vattnet roterar åt olika håll på norra och södra halvklotet. I princip bidrar corioliseffekten till en viss cirkulationsriktning. Noggrant kontrollerade experiment i kärl med 1 m diameter rapporterar resultat som bekräftar en rotation i överensstämmelse med corioliseffekten. I mindre och okontrollerade system där corioliseffekten är jämförelsevis svag, kommer rotationsriktningen att bestämmas av andra faktorer.[8] Oavsett vad som bestämmer riktningen av rotationen så accelereras den på grund av rörelsemängdsmomentets bevarande när vatten sugs in mot avloppet.
Enligt en gammal sägen tillfångatogs en tysk ubåtskapten av de allierade under första världskriget och låstes in i en fönsterlös hytt. Han skulle sedan med handfatets hjälp ha avgjort när båten passerade ekvatorn genom att studera vattenvirveln när han tömde handfatet. Eftersom den horisontella och därmed rotationsdrivande komponenten av corioliskraften är noll utmed ekvatorn, är denna myt intressant ur illustrationssynpunkt men inte historiskt övertygande.
Härledning[redigera | redigera wikitext]
Förhållandet mellan en acceleration i ett inertialsystem och motsvarande acceleration i ett roterande koordinatsystem som roterar enligt rotationshastighetsvektorn kan skrivas
där relationen för tidsderivatan för en vektor i roterande koordinater utnyttjats. Uttrycket
- , gäller för en godtycklig vektor . Då
- ,
blir accelerationen
eller, ekvivalent,
Accelerationen i den roterande referensramen är
Då kraften i den roterande referensramen är
och, enligt definition,
- ,
blir den fiktiva kraften
där den första termen är corioliskraften, den andra termen är centrifugalkraften och den tredje är eulerkraften.
Tyngdkraftspåverkan[redigera | redigera wikitext]

Tyngdkraften är summan av de krafter som verkar på en kropp på grund av gravitationen och jordens rotation. Med utgångspunkt från
(för jordens rotation är eulerkraften noll), kan den effektiva tyngdkraften skrivas som
där är gravitationskraftens värde mätt av en stillastående (icke-roterande) observatör.
Centrifugalaccelerationen är låg jämfört med tyngdaccelerationen. Den når sitt största värde vid ekvatorn där den är cirka 0,3 % av tyngdaccelerationen.
Det framgår av andra termen i högerledet att corioliskraften ger ett positivt eller negativt tillskott beroende på riktningen av .
Referenser[redigera | redigera wikitext]
- Fundamental University Physics Vol. 1 Mechanics by Marcelo, Alonso and Finn, Edward ASIN:B000Z3BT2U
Noter[redigera | redigera wikitext]
- ^ [a b] Alonso/Finn, Mechanics and Thermodynamics, Addison-Wesley, 1967.
- ^ Herbert Goldstein, Classical Mechanics, Addison-Wesley, New York 1950
- ^ V.B. Bhatia, Narosa Publishing House, 1997
- ^ Anders Persson, Fysikaktuellt, Rotation, Corioliseffekten.
- ^ James R. Holton (2004). An Introduction to Dynamic Meteorology. Burlington, MA: Elsevier Academic Press. sid. 64. ISBN 0-12-354015-1. http://books.google.com/?id=fhW5oDv3EPsC&pg=PA64
- ^ Roger Graham Barry & Richard J. Chorley (2003). Atmosphere, Weather and Climate. Routledge. sid. 115. ISBN 0-415-27171-1. http://books.google.com/?id=MUQOAAAAQAAJ&pg=PA115
- ^ Cloud Spirals and Outflow in Tropical Storm Katrina Arkiverad 30 september 2006 hämtat från the Wayback Machine. from Earth Observatory (NASA)
- ^ David J. Van Domelen. ”"Getting Around The Coriolis Force"”. Arkiverad från originalet den 6 mars 2014. https://web.archive.org/web/20140306102750/http://www.algon.dk/dokumenter/coriolis.pdf. Läst 28 februari 2014.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Corioliseffekten.
Wikimedia Commons har media som rör Corioliseffekten.- The coriolis effect in meteorology PDF-file. 5 sidor. En detaljerad förklaring av hur gravitationskraften och jordrotationen påverkar atmosfärens rörelse över jordens yta skriven av Mats Rosengren. 2 figurer. På engelska
- En av SMHI:s sidor om corioliseffekten
- Flush Bosh - an urban legend
- Bad Coriolis
- Bad Coriolis FAQ
- En rimligt enkel förklaring av corioliseffekten
- L R Young: Artificial Gravity Considerations for a Mars Exploration Mission























