Hookes lag
Hookes lag (efter Robert Hooke) är en fysikalisk princip enligt vilken en kraft ger en deformation av mekaniska fjädrar och vissa elastiska material och är proportionell mot avvikelsen från jämviktsläget. Med vektornotation kan Hookes lag skrivas
där F är kraften, k är en konstant och x är förskjutningen från jämviktsläget.
För många material gäller Hookes lag som en första approximation under förutsättning att de elastiska deformationerna är tillräckligt små. Många tekniska konstruktioner är en tillämpning av Hookes lag, till exempel fjädervågar och manometrar.
Hookes lag är grundläggande inom hållfasthetsläran, där för små elastiska deformationer, den mekaniska spänningen σ är proportionell mot töjningen ε:
där konstanten E är elasticitetsmodulen.
Fjäder[redigera | redigera wikitext]
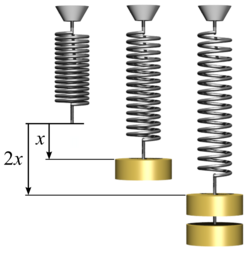
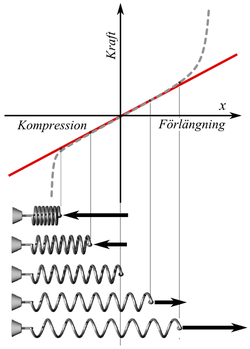
Antag en fjäder vars ena ända är fastsatt och vars andra ända är fritt rörlig, se figur 1. För en idealiserad fjäder är deformationen proportionell mot den kraft som verkar i fjäderns längdriktning enligt
där vektorn F representerar fjäderns återställande kraft, k är fjäderkonstanten i newton per meter (N/m) och x är fjäderns avvikelse från jämviktsläget. Om fjäderns fria ända flyttas från jämviktsläget, kommer den återställande kraft som fjädern utövar att vara riktad mot jämviktsläget.
Om en sträckt eller sammanpressad fjäders fria ända kopplas till en massa, som kan röra sig utan friktion i fjäderns längdriktning, erhålls en harmonisk rörelse, där oscillationens frekvens ökar med ökande styvhet hos fjädern (högre k).
Exempel[redigera | redigera wikitext]
Om fjäderkonstanten är 1 N/m så krävs kraften 1 N för att dra ut fjädern 1 m.
Hookes lag för kontinuerliga kroppar[redigera | redigera wikitext]
Hookes lag kan generaliseras till tre dimensioner. Spänningarna inuti ett kontinuerligt elastiskt material (som hos ett block av gummi eller en metallstång) är förbundna av linjära relationer, som matematiskt liknar Hookes lag och som ofta refererar till detta namn.
Spänningstillståndet hos ett fast ämne kan dock inte beskrivas med en enda vektor. En viss mängd av ett ämne, oavsett dess storlek, kan komprimeras, sträckas och skjuvas samtidigt längs olika eller sammanfallande riktningar.
För att beskriva denna komplexitet måste det relevanta spänningstillståndet i en given punkt representeras av två andra ordningens tensorer, töjningstensorn (i analogi med förskjutningen x) och spänningstensorn (motsvarande den återställande kraften F) och analogin med Hookes lag för en mekanisk fjäder blir då
där är en fjärde ordningens tensor (en linjär mappning mellan andra ordningens tensorer som vanligen kallas styvhetstensor) .

I ett tredimentionellt kartesiskt koordinatsystem, kan töjningsstensorn respektive spänningstensorn representeras av matriserna
Genom att vara en linjär mapping mellan de nio talen och de nio talen , representeras styvhetstensorn av 3×3×3×3 = 81 reella tal . Enligt Hookes lag är då
där och är 1, 2 eller 3.
Alla tre tensorerna varierar från punkt till punkt inom den elastiska kroppen och kan dessutom variera med tiden. Töjningstensorn endast specificerar mediets förskjutningar hos partiklar i punktens omgivning, medan spänningstensorn specificerar de krafter som intilliggande element utövar på varandra. De är därför oberoende av kroppens sammansättning och fysikaliska tillstånd. Styvhetstensorn , är å andra sidan en materialegenskap och beror ofta av fysikaliska tillståndsvariabler som temperatur, tryck och mikroskopiska detaljer.
Beroende på inneboende symmetrier hos , , och , är endast 21 elastiska koefficienter hos dessa oberoende .[1] För isotropiska medier (vilka har fysikaliska egenskaper som är oberoende av riktning), kan reduceras till endast två oberoende tal, bulkmodulen och tvärkraftsmodulen , vilka kvantifierar materialets motstånd mot förändringar i volym respektive tvärkraftsförskjutningar.
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Hookes lag.
Wikimedia Commons har media som rör Hookes lag.
















