Bernoullis lemniskata

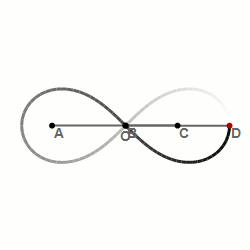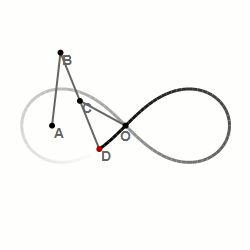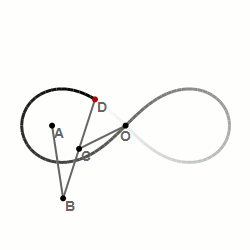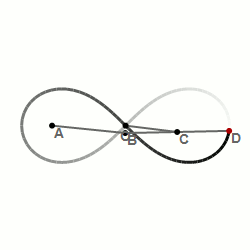
Bernoullis lemniskata

Bernoullis lemniskata är en sluten kurva som liknar oändlighetssymbolen och en liggande 8. Lemniskatan står i ett samband med en liksidig hyperbel.

Alla punkter på kurvan uppfyller ekvationen

$(x^{2}+y^{2})^{2}=2a^{2}(x^{2}-y^{2})$

Med polära koordinater kan samma förhållande skrivas

$r^{2}=2a^{2}\cos 2\theta$

Denna kurva beskrevs första gången 1694 av Jakob Bernoulli som en modifiering av beskrivningen av en ellips. Medan ellipsen utgörs av de punkter som uppfyller villkoret att summan av deras avstånd till de två fokalpunkterna har samma värde, är lemniskatan de punkter som uppfyller villkoret att produkten av deras avstånd till fokalpunkterna har samma värde.

Externa länkar

• Wikimedia Commons har media som rör Bernoullis lemniskata.
  Bilder & media