Bitvis operation

Inom digital datorprogrammering opererar en bitvis operation på ett eller flera bitmönster eller binära tal på bitnivå. Det är snabba primitiva operationer som stöds direkt av processorn och används för att manipulera värden för jämförelser och beräkningar.

På enkla lågkostnadsprocessorer är bitvisa operationer markant snabbare än division, flera gånger snabbare än multiplikation och ibland märkbart snabbare än addition. Medan moderna processorer vanligen adderar och multiplicerar lika snabbt som de utför bitvisa operationer på grund av sina längre pipelines och andra arkitekturer använder bitvisa operationer ofta mindre kraft på grund av ett reducerat användande av resurser.

Bitvisa operatorer

I förklaringarna nedan räknas bitarnas position från höger (den minst signifikanta sidan) till vänster. Det binära värdet 0001 (decimalt 1) har nollor på alla positioner utom den första.

Icke (NOT)

det bitvisa NOT, eller komplementet, är en unär operator som utför logisk negation på varje bit och bildar ettkomplementet till det givna binära värdet. Bitar som är 0 blir 1 och vice versa. Till exempel:

NOT 0111  (decimalt 7)
  = 1000  (decimalt 8)

För osignerade heltal är det bitvisa komplementet (ettkomplementet) till ett tal "spegelbilden" av talet över det osignerade heltalets vidd. Till exempel så är NOT x = 255 - x för osignerade 8-bitars heltal, vilket kan ses som att vända om en ökande följd från 0 till 255 till en minskande från 255 till 0. Ett enkelt, men illustrativt, exempel är att ändra en positiv gråskalebild till en negativ.

Det bitvisa (ett)komplementet är lika med värdets tvåkomplement minus ett. Om tvåkomplementets aritmetik används så är

NOT x = −x − 1.

Och (AND)

Det bitvisa AND tar två binära strängar av samma längd och genomför en logisk AND-operation på varje par av motsvarande bitar genom att multiplicera dem. Så, om båda bitarna har värdet 1, blir resultatet 1 (1 × 1 = 1), annars 0 (1 × 0 = 0). Till exempel

    0101 (decimalt 5)
AND 0011 (decimalt 3)
  = 0001 (decimalt 1)

Operationen kan användas för att avgöra om en viss bit är satt (1) eller ej (0). Till exempel: För att avgöra om den andra biten i 0011 (decimalt 3) är satt använder vi ett bitvist AND med ett tal som bara innehåller en etta i andra biten:

    0011 (decimalt 3)
AND 0010 (decimalt 2)
  = 0010 (decimalt 2)

Eftersom resultatet 0010 inte är noll vet vi att den andra biten i 0011 är satt. Detta kallas ofta "bitmaskning". (En analogi är maskeringstejp som täcker (maskerar) de bitar som inte skall ändras eller delar som är ointressanta. I detta fallet maskerar 0 de bitar vi inte är intresserade av.)

Om vi lagrar resultatet kan det användas för att nollställa valda bitar i ett register. Om vi exempelvis har 0110 (decimalt 6) kan vi nollställa den andra biten genom att använda ett bitvist AND med ett mönster som har en nolla bara i den andra biten:

    0110 (decimalt 6)
AND 1101 (decimalt 13)
  = 0100 (decimalt 4)

På grund av denna egenskap är det lätt att kontrollera ett binärt tals paritet genom att testa värdet hos den minst signifikanta biten. Till exempel:

    0110 (decimalt 6)
AND 0001 (decimalt 1)
  = 0000 (decimalt 0)

Alltså är 0110 (6) jämnt delbart med 2 och alltså jämnt.

Eller (OR)

Ett bitvist OR tar två binära strängar av samma längd och utför en logisk OR-operation på varje par av motsvarande bitar. Resultatet för varje position är 0 om samma bit i de båda talen är 0, annars 1. Till exempel:

   0101 (decimalt 5)
OR 0011 (decimalt 3)
 = 0111 (decimalt 7)

Ett bitvist OR kan användas för att sätta de valda bitarna till värdet 1. Till exempel kan det användas för att sätta en specifik bit (eller flagga) i ett register, där varje bit representerar ett individuellt booleskt värde i ett register. Så kan 0010 (decimalt 2) betraktas som en uppsättning på fyra flaggor, där bara den andra är satt. För att sätta den fjärde flaggan utan att röra de andra gör vi en bitvis OR med 1000 (decimalt 8):

   0010 (decimalt 2)
OR 1000 (decimalt 8)
 = 1010 (decimalt 10)

Den här tekniken är ett effektivt sätt att lagra ett antal booleska värden i så lite minne som möjligt.

Exklusivt eller (XOR)

Ett bitvist XOR tar två binära strängar av samma längd och utför en logisk XOR-operation på varje par av motsvarande bitar. Resultatet blir 1 om den ena biten är 1 och den andra 0, men 0 om båda bitarna är lika. Till exempel:

    0101 (decimalt 5)
XOR 0011 (decimalt 3)
  = 0110 (decimalt 6)

Bitvist XOR kan användas för att invertera ("slå om", som om de vore strömbrytare) valda bitar i ett register, genom att utföra en bitvis XOR med en sträng innehållande 1 på de positioner man vill invertera. Till exempel om man har 0010 (decimalt 2) kan man slå om positionerna två och fyra genom en XOR med 1010:

    0010 (decimalt 2)
XOR 1010 (decimalt 10)
  = 1000 (decimalt 8)

Den här tekninken kan användas för att manipulera bitmönster som representerar booleska tillstånd.

Assemblerprogrammerare använder ibland XOR som en genväg för att sätta värdet på ett register till noll, eftersom detta resultat blir följden om man genomför en XOR på ett tal med sig själv, a XOR a = 0. Många processorer är byggda så att XOR använder färre klockcykler eller mindre minne än att ladda värdet noll och spara det till registret.

Matematiska ekvivalenser

Om x > y för icke-negativa heltal, kan de bitvisa operationerna skrivas som:

${\text{NOT }}x=\sum _{n=0}^{b}2^{n}\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}+1\right){\bmod {2}}\right]$

$x{\text{ AND }}y=\sum _{n=0}^{b}2^{n}\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)$

$x{\text{ OR }}y=\sum _{n=0}^{b}2^{n}\left[\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right){\bmod {2}}\right]{\bmod {2}}\right]$

$x{\text{ XOR }}y=\sum _{n=0}^{b}2^{n}\left[\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\right]{\bmod {2}}\right]$

Där $b$ är antalet bitar i $x=\lfloor \log _{2}x\rfloor +1$ för alla $x\neq 0$.

Atomära booleska funktioner

Inom satslogiken används 3 och 5 (binärt 0011 och 0101) som ingångsvärden, eftersom de motsvarar de möjliga sanningsvärdena hos två atomära satser som skall förbindas med konnektiv. Exempel 0101 AND 0011 = 0001 säger att uttrycket är sant bara när motsvarande bit i de båda talen är 1 (d.v.s. när båda satserna är sanna). För tre satser använder man 15, 51 och 85 (00001111, 00110011 och 01010101). Dessa tal återfinns i taltriangeln  A211344:

           1                                  01
        3     5                       0011          0101
    15    51     85          00001111      00110011      01010101

Bitvis skiftning

Bitskifte betraktas ibland som en bitvis operation, eftersom det behandlar ett värde som en serie bitar snarare än en numerisk storhet. Vid dessa operationer flyttas bitarna (skiftas) åt höger eller vänster. Registerna i en datorprocessor har en fast bredd, så vissa bitar kommer att "skiftas ut" från registrets ena ände, medan samma antal bitar "skiftas in" i den andra. Skillnaden mellan olika skiftoperatorer ligger i vad som skiftas in.

Aritmetiskt skift

Aritmetiskt vänsterskift

Aritmetiskt högerskift

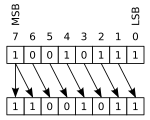
Vid ett aritmetiskt skift tas bitarna som skiftas ut bort. Vid ett aritmetiskt vänsterskift fyller man på med nollor i högeränden, vid ett aritmetiskt högerskift fyller man på med teckenbiten i vänsteränden, så att operandens tecken bevaras.

Exemplet nedan använder ett åttabitarsregister:

   00010111 (decimalt +23) VÄNSTERSKIFT
=  00101110 (decimalt +46)

   10010111 (decimalt −105) HÖGERSKIFT
=  11001011 (decimalt −53)

I första fallet skiftades siffran längst till vänster ut och en nolla skiftades in längst till höger. I andra fallet skiftades ettan längst till höger ut (kanske in i carry-flaggan) och en ny etta kopierades in till höger så att tecknet bevarades. Multipla skift förkortas ibland till en operation med angivande av antal steg. Till exempel:

   00010111 (decimalt +23) VÄNSTERSKIFT-MED-TVÅ
=  01011100 (decimalt +92)

Ett aritmetiskt vänsterskift med n steg är detsamma som att multiplicera med 2ⁿ (förutsatt att overflow ej inträffar), medan ett aritmetiskt högerskift med n steg är detsamma som att dividera med 2ⁿ och runda av mot noll.

Logiskt skift

Logiskt vänsterskift

Logiskt högerskift

Vid ett logiskt skift skiftas nollor alltid in. Ett logiskt vänsterskift är sålunda detsamma som ett aritmetiskt.

Ett logiskt högerskift sätter däremot in nollor i vänsteränden i stället för teckenbiten (som ju kan vara noll), är det bäst för osignerade heltal, medan det aritmetiska är bäst för signerade tvåkomplementära binärtal.

Rotation utan carry

Vänsterrotation

Högerrotation

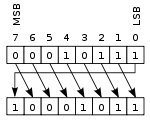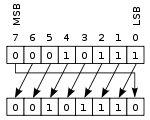
En annan typ av skift är cirkulärt skift eller bitrotation. Vid denna operation "roteras" bitarna som om registrets båda ändar var förenade. Det värde som skiftas in till höger är det värde som skiftades ut till vänster, och vice versa. Den här operationen är användbar om det är viktigt att behålla alla bitarna och används ofta inom digital kryptografi.

Rotation med carry

Vänsterrotation med carry

Högerrotation med carry

Rotation med carry liknar rotation utan carry, med den skillnaden att registrets båda ändar skiljs åt av carry-flaggan. Den bit som skiftas in är carry-flaggans värde före rotationen och den bit som skiftas ut blir carry-flaggans nya värde.

Ett enkelt rotera med carry kan simulera ett logiskt eller aritmetiskt skift om man sätter carryflaggan i förväg. Om man sätter carry-flaggan till noll så är en högerrotation med carry detsamma som ett logiskt högerskift, medan om man i stället sätter carry-flaggan lika med teckenbiten så får man ett aritmetiskt högerskift. Av denna anledning har vissa mikrokontroller såsom PIC bara rotera och rotera med carry och inga speciella aritmetiska eller logiska skiftoperatorer.

Rotera med carry är speciellt användbart när man skall skifta tal som är större än processorns ordlängd, eftersom om ett tal lagras i flera ord så måste den utskiftade biten i det ena ordet skiftas in i det andra. Genom att biten sparas i carry-flaggan är den direkt redo att skiftas in i nästa ord.

Externa länkar

• Joseph Farrell, 2001, Bitwise Operations in C

Referenser

Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia.