Harmonisk oscillator

En harmonisk oscillator är inom fysiken ett oscillerande system där den återdrivande kraften F är proportionell mot avvikelsen från jämviktsläget x0, det vill säga system som kan beskrivas med Hookes lag:
där k är systemets kraftkonstant. Integration ger systemets energi U som en harmonisk, det vill säga kvadratisk, potential:
Om F är den enda kraft som verkar på systemet, är systemet en enkel harmonisk oscillator och undergår en enkel harmonisk rörelse: sinussvängningar kring en jämviktspunkt, med en konstant amplitud och konstant frekvens (oberoende av amplituden). Om en friktionskraft (dämpning), som är proportionell mot hastigheten är närvarande, sägs den harmoniska oscillatorn vara en dämpad oscillator. Beroende på friktionskoefficienten, kan systemet:
- Oscillera med en lägre frekvens än i det icke-dämpade fallets frekvens och amplituden minskar med tiden (underdämpad oscillator).
- Återgå till jämviktsläget utan svängningar (överdämpad oscillator).
Den harmoniska oscillatorn har således egenskapen att svängningens period är oberoende av svängningens amplitud, något som Galileo först lade märke till hos en svängande ljuskrona i en kyrka. Ofta används harmoniska oscillatorn för att idealiserat beskriva approximationer till system som periodiskt växlar läge kring en jämviktspunkt. Många system uppvisar harmonisk svängning i approximationen av små svängningar, till exempel pendeln och atomer i en kristallstruktur.
Klassisk mekanik[redigera | redigera wikitext]
Genom att använda Newtons andra lag F = ma = m d²x/dt² får man en differentialekvation, där lösningen är en sinusvåg som funktion av tid. Den allmänna lösningen kan skrivas som
där A och φ är integrationskonstanter. Oscillationsfrekvensen f = ω/2π är alltså högre för större kraftkonstant och lägre massa.
I vändpunkterna är den potentiella energin och accelerationen maximal, medan hastigheten och kinetiska energin är noll. I punkten med lägst potentiell energi är den kinetiska energin maximal. Energin växlar mellan två olika former. Detta gäller inte bara för potentiell och kinetisk energi, utan kan gälla även för energin i ett elektriskt/magnetiskt fält i en elektromagnetisk svängningskrets. Mängden energi är konstant.
Dämpad harmonisk oscillator[redigera | redigera wikitext]

För verkliga oscillatorer kommer friktion, eller dämpning, att bromsa systemets rörelse. För många svängande system kan friktionskraften Ff modelleras som proportionell mot hastigheten v för objektet: Ff = −cv, där c är den viskösa dämpningskoefficienten.
Newtons andra lag för en dämpad harmonisk oscillator är
Detta kan skrivas om till
där
- kallas oscillatorns odämpade vinkelhastighet och
- kallas dämpningsförhållandet.
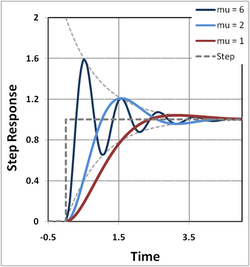
Tiden är i enheter av tidskonstanten τ = 1/(ζω0).
Värdet av dämpningskonstanten ζ bestämmer systemets beteende. En dämpad harmonisk oscillator kan vara
- Överdämpad (ζ > 1): Systemet återvänder, exponentiellt avtagande, mot jämviktsläget utan svängningar. Större värden av dämpningskonstanten ζ leder långsammare till jämvikt.
- Kritiskt dämpad (ζ = 1): Systemet återvänder mot jämviktsläget på så kort tid som möjligt utan svängningar. Detta är ofta det mest önskvärda för dämpning av system sådana som svängdörrar eller äldre tiders analoga mätinstrument, som galvanometrar.
- Underdämpad (ζ < 1): Systemet oscillerar (med en lägre frekvens än för det odämpade fallet) med amplituden gradvis minskande mot noll. Vinkelhastigheten för den underdämpade oscillatorn ges av
Q-värdet för en dämpad oscillator är definierad som
Q är relaterad till dämpningskonstanten genom ekvationen
Kvantmekanik[redigera | redigera wikitext]

För vibrationer av atomer är det dock ofta nödvändigt att tillämpa kvantmekanik. Schrödingerekvationen för en partikel i en harmonisk potential kan lösas exakt. Endast vissa energinivåer är tillåtna och dessa ges av
Den harmoniska oscillatorns grundtillstånd har en vågfunktion med samma form som Gausskurvan. Vågfunktionerna med högre energi har ett antal noder som är lika med kvanttalet .
För mycket höga kvanttal ligger noderna så tätt att strukturen inte har någon betydelse. En glättad kvantmekanisk sannolikhetstäthet är då nästan lika med den klassiska oscillatorns fördelningsfunktion, som har hög sannolikhetstäthet vid de klassiska vändpunkterna, där den klassiska hastigheten är låg. Detta är ett exempel på Bohrs korrespondensprincip.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Harmonisk oscillator.
Wikimedia Commons har media som rör Harmonisk oscillator.













