Projektiv geometri
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2020-04) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
Projektiv geometri är både ett matematiskt ämne och en del av perspektivläran. Projektiv geometri kan beskrivas som förhållandet mellan objekt och den bild som skapas då föremålet projiceras på en yta. En projektion kan t.ex. ofta åskådliggöras genom sin skugga.
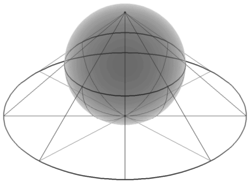
I projektiv geometri finns inga parallella linjer. Eller snarare: alla parallella linjer sammanstrålar/skär varandra i projektionens oändlighet.
Ett plan i projektiv geometri utgör en sluten yta som dels består av punkterna i som finns i själva planet och dels av "linjen i oändligheten". Två projektiva raka linjer skär alltid varandra i precis en punkt, varken mer eller mindre. Det kommer antingen att ske i vad som motsvarar det vanliga planet eller i oändligheten. Inom projektiv geometri förblir normalt sett punkter, linjer och plan desamma när de projiceras. Däremot kan längder, längdförhållanden och vinklar förändras. Se även Desargues sats (1636) och Pappus sats (300-talet e.Kr.).
Den franske matematikern Gérard Desargues (1591–1661) var den förste som formaliserade den projektiva geometrin, med syfte att utvidga den euklidiska geometrin. Han utnyttjade systematiskt element i oändligheten i sin avhandling om kägelsnitt 1639.
Projektiv geometri inom konsten[redigera | redigera wikitext]
Projektiv geometri är en viktig del av perspektivmålning inom konsten och kan t.ex. användas för att föra över en 3D-scen till en 2D-bild. Den italienska arkitekten Leon Battista Alberti (1404–1472) experimenterade med en glasskiva som han placerade mellan sig själv och sitt motiv. Genom att markera (kalkera) vissa punkter på glaset fick han hjälp att skapa en målning med trovärdiga perspektiv.
