Potentiometer

| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-06) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
Potentiometer och reostat är en typ av reglerbara motstånd som främst används för spänningsreglering i kretsar. Bägge har en glidkontakt som ligger an mot en resistiv bana, exempelvis kolbana, och avståndet från den påförda strömmen över banan till glidkontakten avgör resistansen och därmed den utgående spänningen. Skillnaden är att potentiometern har tre kontakter och därigenom fungerar som en spänningsdelare, medan reostaten bara har två. I varje givet läge kan en reostat ersättas med ett fast motstånd, medan en potentiometer ersätts med ett motstånd före och ett motstånd efter T-kopplingen, där summan av de två motståndens resistans blir potentiometerns totala värde. Vidare får en potentiometer samma funktion som en reostat om man inte ansluter den tredje kontakten (jord i bilden till höger).
Potentiometrar finns med flera olika egenskaper, varav de två vanligaste är linjära och logaritmiska. Egenskapen brukar ofta betecknas med en bokstav före motståndsvärdet, till exempel "A500k". Det saknas dock en enhetlig standard. Vissa tillverkare använder A för linjära och B för logaritmiska, medan andra använder A för logaritmisk ("audio") och B för linjär.

Logaritmisk funktion[redigera | redigera wikitext]
Medan en linjär potentiometer är enkel att förstå då resistansen mellan glidkontakten och det gemensamma benet via t.ex. en kolbana är i direkt proportion till den vinkel som potentiometern står på, är en logaritmisk potentiometer något svårare att förstå.
Anledningen till att man har uppfunnit logaritmiska potentiometrar är det sätt på vilket vi människor uppfattar ljudstyrka eller volym. Vår hörsel är kraftigt olinjär dvs. logaritmisk i det avseendet att förändringar av relativ total tystnad är lätta att höra, medan förändringar där ljudnivån redan är hög kräver mer ljudeffekt. Detta borde vara synligt i så kallade isofonkurvor som beskriver örats känslighet för ljudnivåer med avseende på frekvens och styrka.

Enligt vedertagen praxis beskrivs en logaritmisk potentiometers relativa resistans av: där är den procentuella vinkeln som potentiometern är vriden från det att resistansen (R) är Rmax till dess att resistansen är mycket nära noll. Den blir dock i teorin aldrig noll då detta bara existerar i oändligheten hos logaritmiska funktioner. I praktiken blir dock R noll då glidkontakten får kontakt med det gemensamma benet vid full utstyrning.
Av ovanstående formel förstår man att minimal kvot innebär en dämpning på 100 ggr (=10^-2, alpha=1) eller -40dB. Detta är alltså teoretiskt max vad en logaritmisk potentiometer kan dämpa inkommande signal. Om vi omsätter det i praktiken innebär detta att det första steget hos volymratten kommer reglera från till
Men -40 dB motsvarar en resistiv eller spänningsmässig dämpning om 100 gånger. Detta taget i kvadrat motsvarar den effektmässiga dämpningen som alltså är "Maximal uteffekt" delat med tiotusen. Om man således spelar på en förstärkare som maximalt lämnar 50W/kanal (vilket är ganska vanligt) så motsvarar första snäppet på volymratten 5mW. Denna effekt är i paritet med vad vanliga smartphones maximalt levererar ut till lurarna. Betänk då också att de här ska driva högtalare av mycket sämre verkningsgrad. Kort sagt, 5mW hörs knappt i en stereo.
Trim[redigera | redigera wikitext]
I kretsar som behöver balanseras men normalt inte ändras efter det används så kallade trimkomponenter. Dessa brukar vara svåråtkomliga vid normal användning, men kan vid behov justeras. Exempelvis kan frekvensupptagningen i en radio trimmas till att ligga inom det avsedda området, medan den dagliga inställningen av radiokanaler sköts med en vanlig komponent.
Reostat[redigera | redigera wikitext]
Den enklare reostaten tillhör de första reglerbara motstånden, och är oftast avsedda för högre strömstyrkor än potentiometrarna.
-
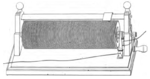
Charles Wheatstones reostat från 1843, en trådinrullad träcylinder med en rörlig strömavtagare ovanför.
-
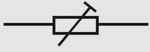
IEC-symbol för reostat.
-
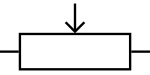
ICE-symbol för trimreostat.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Potentiometer.
Wikimedia Commons har media som rör Potentiometer.