Pappos' sats
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2022-09) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
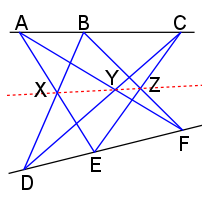
Pappos' sats eller, mera precist, Pappos' hexagonsats är en sats i geometrin. Den är uppkallad efter den grekiske matematikern Pappos, som bevisade satsen första gången omkring år 300. Satsen säger följande:
- Låt A, B och C vara punkter på en linje och D, E och F vara punkter på en annan linje. Då ligger skärningspunkterna X, Y och Z mellan linjerna AE och DB, AF och DC respektive BF och EC på en tredje linje, Papposlinjen.
Dualen till denna incidenssats säger att om man har två skilda mängder av inbördes konkurrenta linjer, A, B och C respektive D, E och F, så är linjerna X, Y och Z, definierade av par av punkter till följd av skärningar mellan linjerna A∩E och D∩B, A∩F och D∩C respektive B∩F ochE∩C, konkurrenta (konkurrens innebär att de löper samman i en punkt).
Pascals sats är en generalisering av Pappos sats, eller snarare så är Pappos' sats specialfallet av Pascals sats när kägelsnittet degenererar till två räta linjer.
Pappos' konfiguration är den konfiguration av nio punkter och nio linjer som uppträder i Pappus' sats, där varje punkt är incident med tre linjer och varje linje är incident med tre punkter. I allmänhet passerar inte Papposlinjen genom de båda andra linjernas skärningspunkt.[1] Denna konfiguration är självdual. Eftersom, speciellt, linjerna BF, CE och XY har samma egenskaper som linjerna X, Y och Z i dualsatsen och kollinearitet mellan X, Y och Z är liktydigt med konkurrens hosBF, CE och XY, är den duala satsen detsamma som satsen själv. Levigrafen för Papposkonfigurationen är Papposgrafen, en bipartit, avståndsreguljär graf med 18 hörn och 27 kanter.
Se även[redigera | redigera wikitext]
Anmärkningar[redigera | redigera wikitext]
- ^ Detta inträffar dock när ABC och DEF är perspektiva, det vill säga att AD, BE och CF är konkurrenta.
