Kägelsnitt

Ett kägelsnitt (konisk sektion) är skärningen mellan ett plan och en cirkulär konisk yta. Beroende på hur planet skär den cirkulära koniska ytan erhålls en ellips, en parabel eller en hyperbel. Detta under förutsättning att planet inte går genom den koniska ytans spets.
Kägelsnittet kan även betraktas som en andragradskurva och används inom till exempel astronomin, för att studera om två kroppar rör sig från eller mot varandra, samt inom paleontologin för att få förståelse för hur ett fossil sett ut. Redan år 200 f.Kr. studerades kägelsnittet grundligt av Apollonios från Perga.
Historia[redigera | redigera wikitext]
Först med att definiera kägelsnittet sägs vara Menaichmos, lärjunge till Platon. Han lär ha definierat kägelsnittet genom att säga att planet som skär konen måste vara vinkelrätt mot generatrisen, linjen som skapar konen. Är vinkeln mellan generatriserna spetsig erhålls en ellips, är vinkeln rät erhålls en parabel och om vinkeln är trubbig erhålls en hyperbel. Observera att man inte kan skapa en cirkel på det här sättet, varför cirkeln på den tiden inte räknades som ett kägelsnitt. Dessvärre finns väldigt få direkta källor till Menaichmos arbete, den främsta källan är ett epigram av Eratosthenes.
Euklides skall också ha arbetat med kägelsnitt och skrivit fyra volymer kring detta, men även dessa är försvunna. Däremot kom greken Apollonios från Perga ut med ”Om koniska sektioner”, åtta volymer som grundligt behandlade kägelsnitten. Dessa finns bevarade och det finns en möjlighet att de första fyra volymerna faktiskt är de verk som Euklides åstadkom. Apollonios sammanfattade nämligen kunskapen om kägelsnitten som fanns på den tiden och utökade den med sina egna idéer, detta var omkring 200 f.Kr. Detta ledde till att det gick att visa att ett plan som skär den cirkulära konen, oberoende av vinkeln mellan generatriserna, skapar ett kägelsnitt, vilket förenklade analysen betydligt.
Apollonios verk översattes till arabiska vilket ledde till att många fler kunde ta del av teorin bakom kägelsnitten. En av dessa var matematikern och poeten Omar Khayyám från Persien som använde kägelsnitt för att lösa algebraiska ekvationer. Detta var dock inte förrän kring 1100 e.Kr.
I början av 1600-talet utökade och använde sig tysken Johannes Kepler av kägelsnitten för att, tillsammans med de observationer dansken Tycho Brahe samlat ihop, dra slutsatsen att planeternas banor faktiskt inte var helt cirkulära utan elliptiska. Även Gérard Desargues och Blaise Pascal skulle komma att spela en viktig roll för utvecklingen av de koniska sektionerna. Pascal följde Desargues tankar och kom fram till ett teorem som idag kallas Pascals teorem. Från detta har många egenskaper hos kägelsnitten kunnat härledas.
Den franske matematikern och filosofen René Descartes införde senare samma århundrade ett rätvinkligt koordinatsystem i kägelsnitten, vilket ledde till att de geometriska figurerna kunde beskrivas med symboler och på så sätt kunde ett geometriskt problem överföras till ett algebraiskt problem. Kägelsnitten kunde nu även ritas upp på ett enkelt sätt med hjälp av koordinatsystemet.

1. Parabel
2. Cirkel och ellips
3. Hyperbel
Tre huvudtyper av kägelsnitt[redigera | redigera wikitext]
Det finns tre huvudtyper av kägelsnitt: parabeln, ellipsen och hyperbeln.
- Parabeln erhålls om ena mantelytan skärs av ett plan som är parallellt med en av generatriserna.
- Ellipsen erhålls om båda generatriserna i en av mantelytorna på konen skärs av planet. Cirkeln, som räknas som en typ av ellips, erhålls endast om planet som skär konen är vinkelrätt mot konens symmetriaxel.
- Hyperbeln erhålls om planet skär båda mantelytorna.
Viktigt är att planet inte i något av ovanstående fall skär den cirkulära konens spets.
Kägelsnitten kan även beskrivas geometriskt i planet genom att betrakta en given punkt i planet, kallat fokus eller brännpunkt, samt en rät linje, kallat direktris eller styrlinje. Observera att brännpunkten inte får ligga på styrlinjen. Då beskriver de punkter, vars avstånd till styrlinjen och brännpunkten står i konstant förhållande e, hur kägelsnittet ser ut.
Beroende på förhållandet e, excentriciteten, genereras olika figurer. För att generera kurvan brukar man säga att man söker orten för alla punkter i planet som uppfyller ett speciellt förhållande e. Det innebär alltså att orten är de punkter som uppfyller ett visst villkor. Cirkeln har en excentricitet lika med noll och därför en styrlinje som ligger i oändligheten.
- En ellips genereras för
- En parabel genereras för
- En hyperbel genereras för
Kägelsnitten, med andra ord andragradskurvor, kan betraktas som plana kurvor som inom den analytiska geometrin och kan beskrivas med ekvationen:
Om diskriminanten är
kan kurvan vara en:
- ellips om
- parabel om
- hyperbel om
Ellipsen[redigera | redigera wikitext]


Ellipsen har en excentricitet mellan 0 och 1 och brukar definieras som orten för de punkter i planet där summan av avstånden till två givna punkter i planet är konstant. De givna punkterna är brännpunkterna (F1 och F2) och genom dem går en linje som kallas storaxeln, vinkelrät mot styrlinjen. Storaxeln skär ellipsen i två punkter kallade vertex (V1 och V2).
Mitt på storaxeln ligger ellipsen centrum, vilket skärs av lillaxeln (y-axeln), som är parallell med styrlinjen och vinkelrät mot storaxeln. Ellipsen är alltså symmetrisk kring storaxeln. Excentriciteten e för ellipsen, kan även betraktas som kvoten mellan avståndet från centrum till brännpunkten och avståndet från centrum till ett vertex,
Inom den analytiska geometrin låter man oftast ellipsen vara placerad så att centrum sammanfaller med origo och att storaxeln motsvaras av x-axeln. Ellipsens ekvation blir då:
där a är avståndet från centrum till vertex, b är avståndet från centrum till punkten där lillaxeln skär ellipsen. c är avståndet från centrum till brännpunkten och med hjälp av ekvationerna
erhålls för e:
Det går även att räkna ut ellipsens parameterlängd, alltså länden på den korda som är parallell med lillaxeln samt skär ena brännpunkten, genom:
Skulle ellipsens centrum slutligen inte sammanfalla med origo utan ligga i är ellipsens ekvation:
Parabeln[redigera | redigera wikitext]

Parabelns excentricitet är lika med 1 och brukar definieras som orten för de punkter i planet som har samma avstånd till brännpunkten (F) som till styrlinjen. Observera att till skillnad från ellipsen har parabeln endast en brännpunkt och ett vertex. Parabeln är symmetrisk kring den linje som går genom brännpunkten och är vinkelrät mot styrlinjen. Denna linje brukar kallas parabelns axel. Skärningspunkten mellan parabeln och axeln kallas vertex (V).
Parabelns form beror endast på avståndet p från brännpunkten till styrlinjen. Avståndet PF och PM kan skrivas som (1) respektive (2).
- (1)
- (2)
Eftersom PF skall vara lika med PM för en parabel sätts (1) lika med (2), vilket leder till (3), som alltså är parabelns ekvation:
- (3)
Parametern för parabeln blir den kortaste kordan som går genom brännpunkten, alltså 2p. Parabelns ekvation kan också beskrivas av (4), där a är avståndet från styrlinjen till vertex.
- (4)
Hyperbeln[redigera | redigera wikitext]

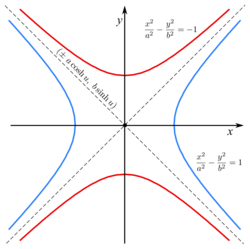
Hyperbelns excentricitet är större än 1 och hyperbeln brukar definieras som orten för de punkter i planet där differensen av avstånden till två givna punkter i planet är konstant. De givna punkterna är, som för ellipsen, brännpunkterna F1 och F2. Genom de båda brännpunkterna går en linje som är symmetrisk till hyperbeln, transversalaxeln (vinkelrät mot styrlinjen), som skär hyperbeln i två vertex (V1 och V2).
Transversalaxelns mitt sammanfaller med koordinatsystemets origo. Till varje hyperbel hör också en konjugathyperbel, med samma centrum som hyperbeln. Axeln genom centrum till konjugathyperbeln kallas konjugataxel. Konjugathyperbelns transversalaxel blir då således hyperbelns konjugataxel.
Inom den analytiska geometrin placeras ofta hyperbelns centrum så att det sammanfaller med origo och så att transversalaxeln motsvaras av x-axeln och konjugataxeln motsvaras av y-axeln. Hyperbelns ekvation blir då
där a är avståndet från centrum till ett av hyperbelns vertex och b är avståndet från centrum till kojugathyperbelns vertex. Låter man c vara avståndet från centrum till en av hyperbelns brännpunkter kan man med hjälp av ekvationerna
bestämma excentriciteten e som
Konjugathyperbelns ekvation är snarlik hyperbelns ekvation och kan skrivas som
En hyperbel har också två asymptoter som korsar hyperbelns centrum (origo). Ekvationerna för asymptoterna blir
Användningsområden[redigera | redigera wikitext]

Kägelsnitten kan ses på många ställen runt om i vår vardag. Reflektorn i en parabolantenn har en genomskärning som är en parabel, en boll man kastar rör sig i en kastparabel och, som nämndes tidigare, används kägelsnitten inom paleontologin för att få en uppfattning om hur till exempel ett fossil sett ut. Även inom optiken kommer kägelsnitten väl till pass, och de används också för att, inom astronomin, bestämma om två kroppar rör sig från eller mot varandra. De kan även användas för att lösa andragradsekvationer.
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
- http://matmin.kevius.com/kagelsnitt.php#elex, Kägelsnitt – andragradskurvor, läst 2011-04-28
- http://www.pererikstrandberg.se/projects/koniska_sektioner.htm, Kägelsnitt, eller koniska, sektioner, läst 2011-04-27
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Kägelsnitt.
Wikimedia Commons har media som rör Kägelsnitt.



























