Liggande stolen

Liggande stolen är en metod för att utföra en division med papper och penna. Det är en matematisk algoritm som kan användas för aritmetisk division av godtyckliga tal. Den är även användbar för polynomdivision inom algebran.
Den liggande stolen är ett exempel på så kallad lång uppställning av division, ibland kallat lång division, och lämpar sig framförallt för uppgifter där nämnaren är flersiffrig. Traditionellt har division med lång uppställning lärts under skolår fyra till sex i den svenska grundskolan. Under senare år har dock skolorna frångått att lära ut lång uppställning, och enligt Skolverket används den idag av endast 1 procent av eleverna.[1] Argumentet för denna förändring är att elever har svårt att förstå lång uppställning samt att kort uppställning (kort division) ofta fungerar för sådana uppgifter som i praktiken beräknas utan räknehjälpmedel.
Fördelen med liggande stolen alt. trappan är att eleverna tränar på den skriftliga kommunikationen. Under räknegången tränar eleven på multiplikation och subtraktion och när de skriver kommer de lättare ihåg. De får även en tydligare förståelse för tiondelar, hundradelar o.s.v. De elever som i framtiden ska läsa på naturvetenskapligt program har stor fördel av att kunna liggande stolen alt. trappan vid beräkningar av polynomdivision.
I liggande stolen placeras nämnaren till höger om täljaren, och introducerades av dåvarande Skolöverstyrelsen år 1979. Den efterträdde då en tidigare uppställning som gått under namnet "trappan", där nämnaren istället placeras till vänster. Trappan rekommenderades av Skolöverstyrelsen från 1955 till 1979, men användes i praktiken i skolorna även under 1980-talet. Matematiskt är trappan och liggande stolen helt likvärdiga, beräkningsstegen är samma, det är bara strukturen som skiljer.
Heltalsdivision[redigera | redigera wikitext]
Till höger finns ett exempel där 764 skall divideras med 4 med hjälp av liggande stolen. Det går till på följande vis:
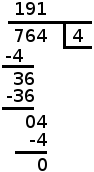
- Vi börjar med att fokusera täljarens första siffra (i det här fallet siffran 7) och se hur många gånger vi kan dela den jämnt med nämnaren (som är 4). Sedan delar vi 7 med 4, vilket genom trunkering blir 1, och denna kvot antecknas på kvotraden rakt över täljarsiffran.
- Divisionen ger också en rest som vi måste räkna ut och sedan ta hand om. Därför får vi multiplicera den just beräknade kvoten (1) med nämnaren (4) igen och anteckna produkten (som blir 4) rakt under vår täljarsiffra.
- Nu kan vi subtrahera denna produkt (4) från den fokuserade täljarsiffran (7) och anteckna resten (3) rakt under. Detta är alltså vad som blev över när vi påstod att 7 delat på 4 bara blir 1, och denna rest får vi ta med oss när vi övergår till att räkna på täljarens nästa siffra.
De tre stegen som beskrivits ovan utgör hela algoritmen. Varje siffra i täljaren ska vi bearbeta på samma sätt, och varje gång det blir en rest, tar vi med oss den till nästa beräkningsrunda. Här kommer runda 2:
- Vi ska nu arbeta med täljarens andra siffra (6). Skriv den direkt efter förra rundans rest (3). Det ger 36 som är den del av täljaren som vi nu ska räkna på. Dela den med nämnaren (4). Det går faktiskt jämnt ut, och kvoten blir 9. Anteckna den på kvotraden rakt över täljarsiffran.
- Nu är det dags att multiplicera kvoten (9) med nämnaren (4) och anteckna produkten (36) rakt under den del av täljaren (36) som vi nu har fokus på.
- Subtrahera sedan produkten (36). Här blir resten 0. Det visste vi redan, eftersom vi märkte att divisionen 36/4 gick jämnt ut.
Tredje och i det här fallet sista rundan görs på samma sätt:
- Flytta ner sista täljarsiffran (4) till resten (0). Det blir 04. Dela 04 på 4 och skriv kvoten (1) på kvotraden.
- Multiplicera kvoten (1) med nämnaren (4). Det blir 4 som skrivs rakt under den täljarsiffra som vi fokuserar.
- Subtrahera 4 från 4 och skriv resten (0) längst ner.
Vi har nu bearbetat alla siffrorna i täljaren och sista beräkningsrundan gav ingen rest. Hela divisionen gick alltså jämnt upp och vi kom fram till att 764/4 = 191.
Om det inte hade gått jämnt upp, om vi alltså fortfarande hade haft en rest att ta hand om, skulle vi få införa decimalkomma och fortsätta algoritmen med decimaler tills resten blev noll. Vi tänker oss då att täljaren skrivs 174,0 eller 174,00 istället för 174. De nya siffror vi då får på kvotraden blir decimaler i kvoten. Vissa divisioner går aldrig jämnt upp utan man får en serie decimaler som ständigt upprepar sig, exempelvis 0,333... eller 0,257257257...
Referenser[redigera | redigera wikitext]
- ^ Att visa vad man kan. En samling artiklar om ämnesproven i år 5, sidan 107, Skolverket, 2004.
