Artificiellt neuronnät
Ett neuronnät (rekommenderad term enligt Svenska datatermgruppen[1]) eller artificiellt neuronnät (ANN) är ett samlingsnamn på ett antal självlärande algoritmer som försöker efterlikna funktionen i biologiska neuronnät (exempelvis hjärnan).
Algoritmer som emulerar neuronnät kan ofta klara problem som är svåra att lösa med konventionella datalogiska metoder. Exempel på tillämpningar är: informationsutvinning (data mining), mönsterigenkänning, signalbehandling, reglerteknik, datorspel, prognoser, självorganisering, icke-linjär optimering, optimeringsproblem med många bivillkor (exempelvis schemaläggning) med mera.
Ett neuronnät måste tränas innan det kan användas. De flesta neuronnät arbetar därför i två faser, först en inlärningsfas där nätverket tränas på den uppgift som ska utföras. Sedan följer en tillämpningsfas där nätverket bara använder det som det har lärt sig. Det går också att låta nätet fortsätta att lära sig även när det används, men vanligen lämnas det som det är när det uppnått den precision som eftersträvades.
Uppbyggnad[redigera | redigera wikitext]
Grundelement[redigera | redigera wikitext]
Alla neuronnät har en grundbyggsten: neuronen (kallas också omväxlande nod, cell, enhet). I konstgjorda neuronnät abstraherar man neuronen till att bestå av en eller flera ingångar (dendriter), en kärna (soma) samt en utgång (axon).
Varje ingång, vj(i), har en vikt wj(i). Grundidén är att en mängd neuroner sitter ihoplänkade i olika strukturer och vikterna ändras vid inlärning. Neuronnät måste tränas upp till önskad funktion.
Kärnan[redigera | redigera wikitext]
I ett artificiellt neuronnätverk är kärnan kraftigt förenklad modell av soma. Kärnan består då av två separata delar, summationsdelen och transferfunktionen. Det finns även en specialingång v0 med vikten w0 som möjliggör justering av alla ingångsvärden (bias[förtydliga]). Ingångarna är anslutna till summationsdelen och utgången (Y(i)) är ansluten till transferfunktionen.
Summation[redigera | redigera wikitext]
Summationsdelen summerar de värden som registrerats på alla ingångar. I denna summering multipliceras varje ingångsvärde med respektive vikt:
Där Θ är bias[förtydliga]-ingången:
Transferfunktion[redigera | redigera wikitext]
Transferfunktionen består av:
- ,
där transferfunktionen kan ha flera olika utseenden: tröskelfunktion, linjärfunktion, sigmoidfunktion, tangens hyperbolicus med flera.
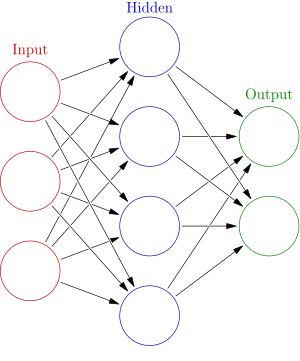
Nätverk[redigera | redigera wikitext]
Ett artificiellt neuronnät består av sammankopplade modeller av neuroner. Neuronnät tränas till önskad funktion. Det innebär att nätverket matas med träningsdata och att neuronernas vikter för varje ingång steg för steg justeras tills vikterna konvergerar.
Tränade nätverk[redigera | redigera wikitext]
Tränade nätverk tränas upp genom att de matas med kända mätdata och kända svar. Om resultatet skiljer sig från det kända svaret beräknas hur stort felet är och vikterna på ingångarna i varje neuron justeras. Detta förfarande itereras och om nätet är rätt designat (där faktorer såsom val av nätverk, antal neuroner, val av träningsdata spelar en avgörande roll) så konvergerar nätet i riktning mot att ge de önskade svaren.
Icke tränade nätverk[redigera | redigera wikitext]
Icke tränade nätverk är självlärande system som används till att hitta kända och okända relationer mellan data. Nätverket matas med data men presenteras inget facit. Vikterna justeras exempelvis beroende på om användarna gillar eller inte gillar resultatet, alternativt baserat på om den process som nätverket styr ger ett resultat nära ett börvärde (om tillämpningen är reglerteknik), eller om en optimeringssfunktion ger maximalt eller minimalt resultat (om tillämpningen är ett optimeringsproblem). Träningen avbryts när viktförändringarna för en iteration konvergerat tillräckligt nära noll.
Tillämpningar[redigera | redigera wikitext]
Neuronnät har en mängd användningsområden, och nya användningsområden skapas hela tiden. Exempel på sådana är:
- Datamining
- Mönsterigenkänning
- Signalbehandling
- Reglerteknik
- Prognoser (till exempel: väderlek (väderprognos), börskurser [se teknisk analys])
- Medicinsk diagnos
- Självorganisering
- Lösning av problem med många/svåra villkor (till exempel schemaläggning, handelsresandeproblemet)
Exempel på artificiella neuronnät samt användningsområde[redigera | redigera wikitext]
| Problem | Nätverk | Beskrivning | Typ av träning |
|---|---|---|---|
| Klassifikation | Learning Vector Quantization, LVQ; Counterpropagation; Självorganiserande kartor, SOM | För att dela in data i bestämda klasser | Kombination av övervakad och oövervakad träning |
| Prognosframställning | Backpropagation | Att kunna ge prognoser om framtida händelser med hjälp av ingångsdata | övervakad |
| Visualisering | Självorganiserande kartor, SOM; Adaptive Resonance Theory, ART | Att åskådliggöra okända korrelationer mellan ingångsdata | oövervakad |
| Association | Hopfieldnät, Hammingnät | Att lära sig mönster och att kunna återskapa störda varianter av dessa | övervakad |
Neuronnätsmodeller[redigera | redigera wikitext]
Perceptronen[redigera | redigera wikitext]
Ett viktigt och mycket enkelt neuronnät är den så kallade perceptronen. Den beskrevs redan på 1950-talet av Frank Rosenblatt.
För att perceptronen skall fungera måste datan vara linjärt separabel.
Det upptäcktes tidigt att perceptronen har begränsad kapacitet att lösa problem. Ett exempel på ett problem som inte kan lösas är XOR.
Flerlagersperceptroner[redigera | redigera wikitext]
Ett sätt att lösa problem som en perceptron inte klarar av, är genom att kombinera flera perceptroner. För att exempelvis lösa XOR kan man kombinera två stycken perceptroner, där ena kan lösa OR och den andra NAND; sedan kombineras perceptronernas utdata för att få XOR.
ART[redigera | redigera wikitext]
Adaptive resonance theory. Bygger på att ett mönster måste resonera med ett tidigare mönster för att läras in.
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Ordlista, Svenska datatermgruppen, hämtat 2011-06-11.
Externa länkar[redigera | redigera wikitext]
- The Nature of Code-kapitel 10(en)
- [1](en)
| |||||||||||||||||||||||||||||||||||||
 Wikimedia Commons har media som rör Artificiellt neuronnät.
Wikimedia Commons har media som rör Artificiellt neuronnät.
Extern litteratur[redigera | redigera wikitext]
- Samling av studier om aktieprediktion med neurala nätverk
- T. Kohonen: Self-Organizing Maps, Springer, 1995
- U. Seiffert & L.C Jain: Self-Organizing Neural Networks, Springer, 2001
- W. Maass & C.M Bishop: Pulsed Neural Networks, MIT Press, 1999
| ||||||||||||||||




