Bézier-kurva


Bézier-kurva är en matematisk uträkning av en kurva. Begreppet används inom den matematiska grenen numerisk analys, och själva Bézierkurvorna är mycket vanligt förekommande inom datorgrafik (inklusive CAD-system[1]).
Den genombrytande insikten som ledde fram till Bézier-kurvan var att istället för att definiera kurvan med punkter som ligger på kurvan, så använder man så kallade kontrollpunkter nära kurvan. Kontrollpunkterna bildar en kontrollpolygon. Istället för att ändra kurvan direkt, kan man istället ändra kontroll-polygonen och kurvan följer på ett intuitivt sätt[2]. Bézier-kurvan är en parametriserad kurva som använder Bernsteins polynom som bas. Det är intuitivt att tänka sig parametrisering av tiden, där kontrollpunkterna bestämmer riktningen och farten av kurvan.[3]
Historik och användning[redigera | redigera wikitext]
Bézier-kurvor användes och utvecklades först inom bilindustrin för att lösa problem med att rita och presentera ritningar på datorn. År 1959 anställde det franska företagen Citroën matematikern Paul de Faget de Casteljau. De Casteljau anpassade Bernsteinpolynomet för sin definition av kurvorna och utvecklade den nu kallade de Casteljau-algoritmen. Att hans arbete inte blev känt förrän senare berodde på att Citroën höll hans arbete hemligt under en lång tid. Istället var det Pierre Bézier som fick ge namn åt Bézier-kurvan. Bézier som ledde designavdelningen Rénault, ett annat franskt företag, jobbade självständigt och utvecklade en kurva som visade sig vara identisk med de Casteljaus.[2]
Inom vektorgrafik är Bézierkurvor ett viktigt verktyg. De används för att skapa modeller med rundade kurvor som kan skalas obegränsat, utan att förlora kvalitet. Banor, som de ofta kallas i olika bildbehandlingsprogram som Adobe Illustrator, Adobe Photoshop och GIMP, är kombinationer av Bézier-kurvor som lagts ihop och bildar längre linjer. Dessa banor har inte samma restriktioner som rastergrafik och är intuitiva att använda. De används också inom animering som ett verktyg för att kontrollera rörelse i applikationer som Adobe Flash, Adobe After Effects och Autodesk 3ds Max.
Generell definition med exempel.[redigera | redigera wikitext]
För Bézier-kurvan utnyttjas Bernstein's polynom som grund. Med en given sekvens av punkter representeras Bézier-kurvan av grad n (order n+1) av
där
är Bernstein-polynomet och där är binomialkoefficienter. [4]
Punkterna är ett set av kontrollpunkter där den första respektive den sista alltid är start- och ändpunkterna på kurvan. Kurvan behöver inte passera igenom de andra punkterna, utan de punkterna utnyttjas för att ge information om i vilken riktning och hastighet kurvan ska röra sig.

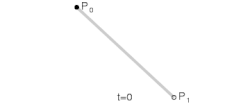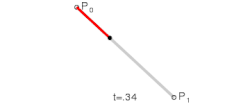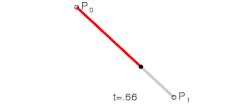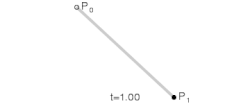
I det enklaste fallet har man två stycket kontrollpunkter och som bildar en rät linje.
För n=2 fås alltså tre kontrollpunkter och en så kallad kvadratisk Bézier-kurva:
För n=3 fås en kubisk Bézier-kurva:

Kurvan kan också representeras genom matriser, som till exempel för n=3 enligt
Egenskaper hos Bézier-kurvan.[redigera | redigera wikitext]
Bézier-kurvan är invariant under affin avbildning. Om man vill transformera kurvan behöver man alltså bara avbilda kontrollpunkterna . Denna egenskap är speciellt viktig inom grafiken: då man ska beräkna en kurva som till exempel blivit roterad behöver man bara avbilda kontrollpunkterna och sedan beräkna kurvan utifrån avbildningen.
En annan egenskap är att kurvan tangerar kontroll-polygonen som skapas mellan kontrollpunkterna . Detta kan ses av förstaderivatan:
Speciellt och .
Med Bézier-kurvans kontrollpunkter kan man också skapa ett konvext hölje i vilket kurvan alltid kommer befinna sig. Denna egenskap kan vara väldigt effektiv vid skärningsproblem. Om man till exempel vill se om kurvor skär varandra kan man utesluta alla kurvor där höljena inte skär varandra, alltså om den konvexa mängden inte delar några element. [5]
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
- ^ ”Bezierkurvor”. cs.umu.se. http://www.cs.umu.se/kurser/TDBB19/VT05/OH-bilder/Bezier.pdf. Läst 31 januari 2016.
- ^ [a b] Gerald Farin. A History of Curves and Surfaces in CAGD. http://kowon.dongseo.ac.kr/~lbg/cagd/history1.pdf.
- ^ [a b] Dr.P. V. Madhusudhan (26 oktober 2010). ”Lec-46 Parametric Bezier Curve”. NPTEL. https://www.youtube.com/watch?v=-J2m_ugWNtc&t=1801s. Läst 14 maj 2017.
- ^ M. Patrikalakis, Nicholas. Shape Interrogation for Computer Aided Design and Manufacturing. http://web.mit.edu/hyperbook/Patrikalakis-Maekawa-Cho/. Läst 15 maj 2017
- ^ Agoston, Max K. (2005-12-06) (på engelska). Computer Graphics and Geometric Modelling: Implementation & Algorithms. Springer Science & Business Media. ISBN 9781846281082. https://books.google.se/books?id=TAYw3LEs5rgC&pg=PA404&redir_esc=y#v=onepage&q&f=false. Läst 15 maj 2017


![{\displaystyle \mathrm {B} (t)=\sum _{i=0}^{n}b_{i,n}(t)\mathrm {P} _{i},\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6608f4179f9a00e707c7ab92df77f8a12df66eb7)






![{\displaystyle \mathbf {B} (t)=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1},\quad t\in [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b9fd460ddc3034aacb79928a0c2430f672284d1)

![{\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2},\quad t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c955149cdd45dc451fa20197947aacc206ad37d3)
![{\displaystyle \mathbf {B} (t)=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t\mathbf {P} _{1}+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3},\quad t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc076a09bf3595a1db894268df292c21ff5fa81)



