Rät linje
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-09) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
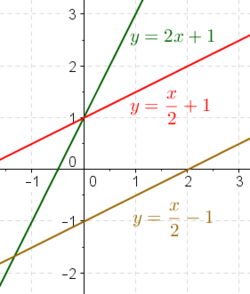
En rät linje, ofta benämnd enbart linje, är en kurva, där närmaste vägen mellan två punkter på kurvan går utefter linjen. Den räta linjen har oändlig utsträckning åt båda håll, till skillnad mot en sträcka, som begränsas av två punkter på linjen som bildar sträckans ändpunkter, eller en stråle, som enbart begränsas av en punkt och utifrån den har en given riktning. En förflyttning mellan två punkter som sker längs en rät linje är en rätlinjig förflyttning.
Definition[redigera | redigera wikitext]
I linjär algebra kan man representera en rät linje som en punkt, eller som en ortsvektor till en punkt, på linjen, plus en multipel av en riktningsvektor för linjen. Detta kan beskrivas med uttrycket:
och där b inte är nollvektorn.
Riktningsvektorn spänner upp linjen. Man kan brukar säga att en linje har 1 frihetsgrad.
Euklides definierade en linje som en längd, utan bredd.
Olika geometrier[redigera | redigera wikitext]
Vad som anses som kortaste avståndet avgörs av vilken geometri man sysslar med. I icke-euklidisk geometri gör man avsteg från den intuitiva föreställningen av vad en rät linje är. Så är till exempel storcirklar (bland annat ekvatorn och meridianer) på en sfärisk yta (exempelvis jordytan) att betrakta som räta linjer för den geometri som sysslar enbart med punkter på den sfäriska ytan.
Elliptisk geometri[redigera | redigera wikitext]
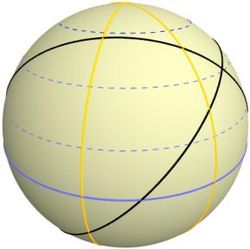
I elliptisk geometri, det vill säga den geometri som sysslar enbart med punkter på den sfäriska ytan, existerar inga parallella linjer, vilket bryter mot parallellaxiomet. Eftersom alla linjer i denna geometri är storcirklar kommer de förr eller senare att skära varandra.
-
En triangel (med tre räta sidor) och två parallella linjer i det hyperbolska rummet.
Se även[redigera | redigera wikitext]
- Linjär ekvation (räta linjens ekvation)
- Enpunktsformen
- Elastiska linjens ekvation
- Sfärisk geometri
- Plücker-koordinater


