Vågekvation

En vågekvation är en partiell differentialekvation som beskriver beteendet hos olika typer av vågor, som exempelvis ljudvågor, ljusvågor och vattenvågor.
I en dimension är den homogena vågekvationen:
Den generella lösningen till denna ekvation är
vilken kan beskriva alla endimensionella vågor. beskriver en i högra riktningen gående våg med hastigheten , medan beskriver en vänstergående våg med samma hastighet.
Härledningar[redigera | redigera wikitext]
Härledning från Hookes lag[redigera | redigera wikitext]
I det endimensionella fallet kan vågekvationen härledas från Hookes lag. Antag en följd av små vikter med massan m sammanbundna med masslösa fjädrar med längden h och vars fjäderkonstanter är k:
Den beroende variabeln u(x) anger avståndet från jämviktspunkten till massan placerad i x, så att u(x) väsentligen mäter storleken av en störning (sträckning) som färdas genom ett elastiskt material. Krafterna som utövas på massan m i positionen x+h är
Ekvationen för rörelsen i positionen x+h fås genom att sätta dessa två krafter som lika:
där tidsberoendet hos u(x) gjorts explicit.
Om raden av vikter består av N vikter jämnt fördelade över längden L = Nh med den totala massan M = Nm och den totala fjäderkonstanten för raden är K = k/N kan ekvationen skrivas
Med gränsvärdena N → ∞, h → 0 och antagandet att funktionen är överallt deriverbar blir detta
i enlighet med definitionen av andraderivata. (KL2)/M är kvadraten på utbredningshastigheten i detta speciella fall.
Algebraisk metod[redigera | redigera wikitext]
Den en-dimensionella vågekvationen är ovanlig för en partiell differentialekvation såtillvida att en relativt enkel lösning kan hittas. Genom definition av två nya variabler[1]
ändras vågekvationen till
vilket leder till den allmänna lösningen
eller, ekvivalent
Med andra ord, lösningar till den endimensionella vågekvationen är summan av en funktion F som rör sig till höger och en funktion G som rör sig åt vänster. "Rör sig" betyder att dessa individuella och godtyckliga funktioner är konstanta med avseende på x; emellertid translateras funktionerna till vänster respektive höger med tiden och med hastigheten c. Detta häleddes av Jean le Rond d'Alembert.[2]
Ett annat sätt att erhålla detta resultat är att notera att vågekvationen kan "faktoriseras":
och därmed är
De två sista funktionerna är advektionsekvationer, som rör sig åt vänster respektive åt höger, båda med den konstanta hastigheten c.
För ett initialvärdesproblem kan de godtyckliga funktionerna bestämmas för att uppfylla de initiala villkoren:
Resultatet är d'Alemberts formel:
I den klassiska meningen, att om f(x) ∈ Ck och g(x) ∈ Ck−1 då gäller att u(t, x) ∈ Ck. Emellertid, vågformerna F och G kan vara generaliserade funktioner, sådana som delta-funktionen. I det fallet, kan lösningen tolkas som en impuls som färdas till vänster eller höger.
Den grundläggande vågekvationen är en linjär differentialekvation och superpositionsprincipen kan tillämpas, vilket innebär att förskjutningarna orsakade av en eller flera vågor är summan av de individuella vågornas förskjutningar. Dessutom kan beteendet hos en våg analyseras genom att dela upp vågen i komponenter.
Se även[redigera | redigera wikitext]
- Partiell differentialekvation
- Partiell derivata
- Värmeledningsekvation
- Schrödingerekvationen
- Vågrörelse
- Maxwells ekvationer
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Eric W. Weisstein. ”d'Alembert's Solution”. MathWorld. http://mathworld.wolfram.com/dAlembertsSolution.html. Läst 21 januari 2009.
- ^ D'Alembert (1747) "Recherches sur la courbe que forme une corde tenduë mise en vibration" (Researches on the curve that a tense cord forms [when] set into vibration), Histoire de l'académie royale des sciences et belles lettres de Berlin, vol. 3, pages 214–219.
- See also: D'Alembert (1747) "Suite des recherches sur la courbe que forme une corde tenduë mise en vibration" (Further researches on the curve that a tense cord forms [when] set into vibration), Histoire de l'académie royale des sciences et belles lettres de Berlin, vol. 3, pages 220–249.
- See also: D'Alembert (1750) "Addition au mémoire sur la courbe que forme une corde tenduë mise en vibration," Histoire de l'académie royale des sciences et belles lettres de Berlin, vol. 6, pages 355–360.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Vågekvation.
Wikimedia Commons har media som rör Vågekvation.






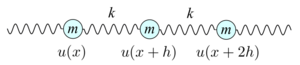

![{\displaystyle F_{\mathit {Hooke}}=F_{x+2h}-F_{x}=k\left[{u(x+2h,t)-u(x+h,t)}\right]-k[u(x+h,t)-u(x,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/128dccc346b1598cd2332a2eee4c0c8acfd6ca57)
![{\displaystyle {\partial ^{2} \over \partial t^{2}}u(x+h,t)={k \over m}[u(x+2h,t)-u(x+h,t)-u(x+h,t)+u(x,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03475672d64f1c412bad36c0f800a70b6fec6057)






![{\displaystyle \left[{\frac {\partial }{\partial t}}-c{\frac {\partial }{\partial x}}\right]\left[{\frac {\partial }{\partial t}}+c{\frac {\partial }{\partial x}}\right]u=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64871fbed80a7f222c71a96de523a60a71bf9a23)



