Monte Carlo-metod
Monte Carlo-metoder är ett samlingsnamn för en typ av matematiska algoritmer som bygger på slumptal. Monte Carlo-metoder kan användas för att lösa vissa problem som är svåra att lösa med konventionella deterministiska metoder, bland annat för att simulera fysikaliska system (till exempel molekyldynamik) eller göra vissa statistiska beräkningar. Idén med att använda slumpen i beräkningarna är att göra beräkningar som i genomsnitt ger det rätta svaret, även om resultatet för varje enskild beräkning är slumpmässig. Monte Carlo-metoder har därför ofta en upprepande natur, och den stora mängden beräkningar gör dem lämpliga att utföras av datorer.
Historia[redigera | redigera wikitext]
Idén att använda slumptal för att utföra beräkningar utvecklades i Manhattanprojektet under andra världskriget.[1] Syftet var att simulera hur grupper med fysikaliska partiklar rör sig, som ett led i utvecklingen av atombomben. Mer specifikt var syftet att lösa diffusionsekvationen i samband med bestämning av reaktorfysikaliska parametrar, i första hand multiplikationskonstanten i termiska, heterogena kärnreaktorer. Sedan dess har metoderna utvecklats i flera olika riktningar, och hittat tillämpningar inom många olika områden där olika typer av beräkningar behöver utföras.
Namnet Monte Carlo-metod myntades från kasinot i Monte Carlo, där beteendet hos upprepade slumpmässiga experiment också är centralt.
Exempel[redigera | redigera wikitext]
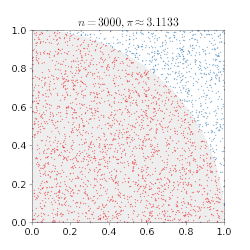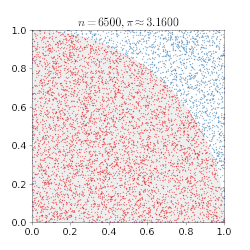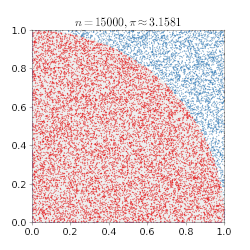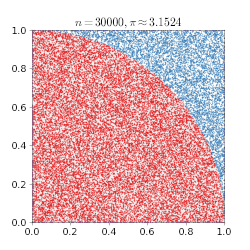
En Monte Carlo-metod kan användas för att bilda ett närmevärde för π: enligt formeln för cirkelns area är arean av en kvartscirkel med radien 1 exakt ¼π. Placeras en kvartscirkel i en kvadrat med sidan och arean 1, som i figuren, kommer andelen av kvadraten som ligger i kvartscirkeln att vara samma som dess area. Genom att slumpmässigt generera likformigt fördelade punkter i kvadraten och räkna hur många av dem som hamnar inuti kvartscirkeln kan andelen uppskattas, och därmed arean på kvartscirkeln. Ju fler punkter som genereras desto bättre blir uppskattningen, enligt de stora talens lag. Om uppskattningen multipliceras med 4 får man en uppskattning av π.
Definition[redigera | redigera wikitext]
Det saknas konsensus om hur Monte Carlo-metoder ska definieras, men det är åtminstone beräkningar som innefattar slumptal på något sätt. Många Monte Carlo-metoder kan formuleras som att de i något steg approximerar integralen där är en godtycklig funktion och är mått över (till exempel en sannolikhetsfördelning), med den numeriska approximationen där är (möjligen viktade) slumptal med fördelning enligt . Med hjälp av stora talens lag kan man bevisa att approximationen konvergerar mot när . Typiskt används Monte Carlo-metoder när integralen inte går att lösa analytiskt, utan numeriska approximationer krävs. I förhållande till andra numeriska approximationer som inte bygger på slumptal är Monte Carlo-metoder jämförelsevis effektivare när problemets dimensioner (dimensionen på ovan) ökar.[2]
Den tekniska utmaningen i att konstruera en Monte Carlo-metod för ett problem är ofta att generera slumptalen .
Avancerade Monte Carlo-metoder[redigera | redigera wikitext]
Markovkedje-Monte Carlo[redigera | redigera wikitext]
Markovkedje-Monte Carlo (eller på engelska, Markov Chain Monte Carlo, MCMC) är en familj med metoder för att generera slumptal från sannolikhetsfördelningar. MCMC är framför allt användbara när fördelningen endast går att utvärdera punktvis, vilket till exempel kan vara fallet för statistiska modeller. De två grundläggande metoderna är Gibbs sampling[3] (från 1980-talet) och Metropolis-Hastings-samplern[4][5] (som i princip kom med de första Monte Carlo-metoderna från 1940-talet). Några senare utvecklade metoder är Hamiltonsk Monte Carlo,[6][7] slice sampling[8] och bouncy particle sampler.[9]
Sekventiell Monte Carlo[redigera | redigera wikitext]
Sekventiell Monte Carlo (SMC) är, likt MCMC, en metod för att generera slumptal från sannolikhetsfördelningar. SMC utvecklades inom signalbehandling på 90-talet för att göra filtrering i tillståndsmodeller[10] och har sedan 00-talet generaliserats till att bli ett lika mångsidigt verktyg som MCMC,[11] som har blivit populärt inom bland annat maskininlärning.
Tillämpningar[redigera | redigera wikitext]
Monte Carlo-metoder används för att lösa problem inom många olika vetenskaper, bland annat fysik, maskininlärning, signalbehandling, mekanik, beräkningsbiologi, klimatologi, datorgrafik, tillämpad statistik, artificiell intelligens och ekonometri.
Litteratur[redigera | redigera wikitext]
- "Monte Carlo Statistical Methods", Christian Robert och George Casella, 2004
- Art B. Owen (2013). ”Monte Carlo theory, methods and examples”. http://statweb.stanford.edu/~owen/mc/.
Referenser[redigera | redigera wikitext]
- ^ Nicholas Metropolis och Stanisław Ulam (1949). ”The Monte Carlo Method”. Journal of the American Statistical Association 44 (247).
- ^ ”Monte Carlo theory, methods and examples”. statweb.stanford.edu. http://statweb.stanford.edu/~owen/mc/. Läst 6 mars 2018.
- ^ Geman, S.; Geman, D. (1984). ”Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images”. IEEE Transactions on Pattern Analysis and Machine Intelligence 6 (6): sid. 721–741. doi:.
- ^ Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. (1953). ”Equations of State Calculations by Fast Computing Machines”. Journal of Chemical Physics 21 (6): sid. 1087–1092. doi:. https://semanticscholar.org/paper/f6a13f116e270dde9d67848495f801cdb8efa25d.
- ^ Hastings, W.K. (1970). ”Monte Carlo Sampling Methods Using Markov Chains and Their Applications”. Biometrika 57 (1): sid. 97–109. doi:.
- ^ Duane, Simon; Kennedy, A.D.; Pendleton, Brian J.; Roweth, Duncan. ”Hybrid Monte Carlo”. Physics Letters B 195 (2): sid. 216–222. doi:. https://doi.org/10.1016/0370-2693(87)91197-X. Läst 6 mars 2018.
- ^ Betancourt, Michael (2017-01-09). ”A Conceptual Introduction to Hamiltonian Monte Carlo”. arXiv:1701.02434 [stat]. http://arxiv.org/abs/1701.02434. Läst 6 mars 2018.
- ^ Neal, Radford M. (2003-06). ”Slice sampling” (på engelska). The Annals of Statistics 31 (3): sid. 705–767. doi:. ISSN 0090-5364. https://projecteuclid.org/euclid.aos/1056562461. Läst 6 mars 2018.
- ^ Bouchard-Côté, Alexandre; Vollmer, Sebastian J.; Doucet, Arnaud (2015-10-08). ”The Bouncy Particle Sampler: A Non-Reversible Rejection-Free Markov Chain Monte Carlo Method”. arXiv:1510.02451 [math, stat]. http://arxiv.org/abs/1510.02451. Läst 6 mars 2018.
- ^ Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. (1993-04-01). ”Novel approach to nonlinear/non-Gaussian Bayesian state estimation” (på engelska). IEE Proceedings F Radar and Signal Processing 140 (2). doi:. ISSN 2053-9045. http://dx.doi.org/10.1049/ip-f-2.1993.0015. Läst 6 mars 2018.
- ^ Del Moral, Pierre; Doucet, Arnaud; Jasra, Ajay (2006). ”Sequential Monte Carlo Samplers”. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 68 (3): sid. 411–436. http://www.jstor.org/stable/3879283. Läst 6 mars 2018.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Monte Carlo-metod.
Wikimedia Commons har media som rör Monte Carlo-metod.











