Primtalsfaktorisering
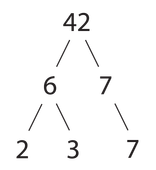
Primtalsfaktorisering innebär att ett heltal skrivs som en produkt av primtal. Exempelvis har talet 456 faktoriseringen
Enligt aritmetikens fundamentalsats har varje positivt heltal en primtalsfaktorisering som är unik om man bortser från faktorernas inbördes ordning.
Heltalsfaktorisering kallas den allmännare process i vilken ett heltal skrivs som en produkt av mindre men inte nödvändigtvis prima heltal. Till skillnad från primtalsfaktorisering är resultatet av en heltalsfaktorisering inte alltid unikt. Till exempel är både och giltiga heltalsfaktoriseringar av talet 12.
Algoritmer[redigera | redigera wikitext]
Ett flertal algoritmer används för primtalsfaktorisering. Den enklaste att förstå är trial division, vilken innebär att man för ett tal n testar att dividera n med varje tal upp till och med .[1] De tal som ger resten noll är faktorer av n. Trial division är den överlägset effektivaste metoden för att bestämma små faktorer, exempelvis mindre än 109, men oanvändbart för att hitta väsentligt större faktorer. Lyckligtvis är metoden effektiv för slumpmässigt valda tal, eftersom hälften av alla tal har 2 som faktor, en tredjedel har 3 som faktor, och så vidare. Hela 88 % av alla heltal har minst en faktor som är mindre än 100. Trial division kan därför användas för att snabbt röja undan små faktorer varefter en mer avancerad algoritm tar hand om de återstående.[2]
Rationellt såll är en generell algoritm för primtalsfaktorisering. Den är ett specialfall av det generella talsållet (general number field sieve, GNFS), och medan den är mindre effektiv än den allmänna algoritmen så är den konceptuellt enklare.
De enklaste metoderna för att snabbt hitta faktorer något större än cirka 10 siffror är Pollards rho-metod[3] och Pollards p-1-metod samt varianter av dessa. För faktorer i storleksordningen 20–25 siffror är ECM (faktorisering med elliptiska kurvor) ytterligare ett alternativ. De enda praktiska algoritmerna för större faktorer än så är varianter av Eratosthenes såll, kvadratiska såll och talkroppssåll. Effektivast för stora tal är general number field sieve (GNFS), som används för att faktorisera RSA-tal med 100-siffriga faktorer.[4]
Tillämpbarhet[redigera | redigera wikitext]
Det tycks som om det beräkningsmässigt är betydligt svårare att bestämma primtalsfaktorerna till ett givet tal än att multiplicera ihop faktorer. Det är också enklare att med ett primtalstest avgöra huruvida ett tal kan delas upp i mindre faktorer än att om så är fallet bestämma faktorerna. Datorer kan idag enkelt multiplicera tal med miljontals siffror och utföra primtalstest på tal med tusentals siffror, men att faktorisera ett 100-siffrigt tal är ett utmanande problem. Svårigheten att faktorisera heltal utnyttjas av krypteringsalgoritmer som RSA.[5][6]
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Mollin, Richard A. (2002). ”A brief history of factoring and primality testing B. C. (before computers)” (på engelska). Mathematics Magazine 75 (1): sid. 18–29. doi:. Läst 26 september 2019.
- ^ Crandall, Richard; Pomerance, Carl (2005) (på engelska). Prime numbers. A computational perspective (2:a). New York, NY: Springer-Verlag. ISBN 0-387-25282-7
- ^ Pollard, J. M. (1975). ”A Monte Carlo method for factorization” (på engelska). BIT Numerical Mathematics 15 (3): sid. 331–334. doi:. Läst 26 september 2019.
- ^ Carl Pomerance (1982). ”Analysis and Comparison of Some Integer Factoring Algorithms” (på engelska). Mathematical Centre tracts 154: sid. 89-139.
- ^ D. Brown (2005). ”Breaking RSA may be as difficult as factoring” (på engelska). http://eprint.iacr.org/2005/380. Läst 26 september 2019.
- ^ Dan Boneh, Ramarathnam Venkatesan (1998). ”Advances in Cryptology — EUROCRYPT'98” (på engelska). Lecture Notes in Computer Science (Springer) 1403. doi:. Läst 26 september 2019.
Tryckta källor[redigera | redigera wikitext]
- Kodboken, Simon Sing. Kryptografins historia där RSA-kryptering nämns.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Primtalsfaktorisering.
Wikimedia Commons har media som rör Primtalsfaktorisering.
| ||||||||||||||||||||||||||





