Newtons metod
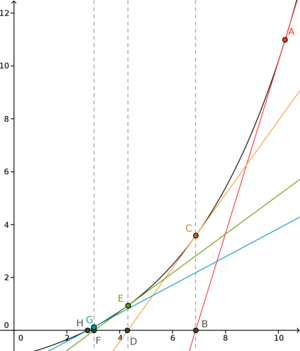
Funktionen f(x) = e^(x/4) - 2 analyseras med början i x=10,25.
A=(10,25, 10,98), C=(6,87, 3,57), E=(4,31, 0,94), H=(2,78, 0). Det sökta svaret med två värdesiffror är (2,77, 0).
Newtons metod, eller Newton–Raphsons metod (efter Isaac Newton och Joseph Raphson) är en numerisk metod för att approximera nollställen till en funktion. Man använder alltså en numerisk metod för att hitta en rot till en ekvation, vilken går ut på att man väljer en punkt på kurvan som man räknar ut tangenten för. Det x-värde vid vilket tangenten skär x-axeln används sedan för att räkna ut en ny tangent i en iterativ process till dess att önskad noggrannhet uppnåtts.
Tangenten till en funktion i punkten har enligt enpunktsformeln ekvationen
Den skär x-axeln då y = 0, dvs:
Iterationsformeln blir alltså
Beskrivning[redigera | redigera wikitext]

Idén är att steg för steg beräkna bättre och bättre approximationer till en rot till en ekvation . Vi börjar med en approximation . Tangenten tillhörande funktionen f i punkten skär x-axeln i en punkt (förutsatt att ) som betecknas . Man bestämmer denna punkt genom formeln
där är värdet av derivatan till f i , och så itererar man förloppet med som startpunkt, och så vidare. Den allmänna formeln blir då
Talföljden konvergerar mot en rot r förutsatt att är tillräckligt nära den rot som ska approximeras.
Blir derivatans värden svårberäknade kan man approximera dem med formeln:
eller mer exakt approximation med
Exempel[redigera | redigera wikitext]
Kvadratroten ur ett tal
Hur hittar man kvadratroten ur ett tal?. Det finns åtskilliga metoder för att hitta rötter och Newton Raphsons metod är en.
T.ex. om man önskar hitta kvadratroten ur 1395, så är det ekvivalent med att:
Funktionen i Newton Raphsons metod blir då,
med derivatan,
Med en inledande gissning 12, så blir ordningsföljden enligt Newton Raphsons metod:
Dvs
Där de korrekta siffrorna är understrukna. Vi ser här att bara med några få iterationer så får vi fram en lösning som stämmer överens på många decimaler.
Väljer vi att i samma funktion som i exemplet ovan
Som vi ser så går funktion mot oändligheten då x går mot noll.
Väljer vi att
Här ser vi att funktionen för både noll och x. Detta implicerar då att Newton-Raphsons metod endast fungerar om den inledande gissningen är större än noll dvs och mindre än oändligheten dvs Så vårt intervall borde då vara
Historia[redigera | redigera wikitext]
Redan på Babylons tid visste man hur man kunde approximera rötter och rotberäkningar förekom också i de tidiga kulturerna i Egypten, Kina, Indien (Aryabhata) och Grekland (Heron). I Indien finns metoder för att beräkna närmevärden till kvadratrötter beskrivna på 500-talet f.Kr., i bland annat Baudhayanasutran.
Men det var Newton och Raphson som använde sig av analys för att generalisera denna urgamla metod för att hitta rötterna till en godtycklig ekvation. Newtons metod publicerades först år 1685 i boken A Treatise of Algebra both Historical and Practical av John Wallis. 5 år senare publicerade Joseph Raphson en förenklad version i avhandlingen Analysis aequationum universalis. Där Raphson visade att det är algebraisk metod som är begränsad till polynom. Newtons metod har också beskrivits av Isaac Newton år 1669 i sin bok De analysi per aequationes numero terminorum infinitas (som publicerades 1711 av William Jones) och i De metodis fluxionum et serierum infinitarum(författad 1671, översatt och publicerad som Method of Fluxions år 1736 av John Colson). Men det ska nämnas att den beskrivning som Newton gav i de ovannämnda böckerna skiljer sig mycket från den beskrivning som har angivits ovan.
Referenser[redigera | redigera wikitext]
- Forsling & Neymark, Matematisk Analys En variabel, 228-229, ISBN 91-47-05188-4
- Författarna och Liber AB, Tabeller och formler för NV- och TE- Programmen femte upplagan, S 56, ISBN 978-91-47-01746-1
- Engelska wikipedias beskrivning av Newton Raphsons metod http://en.wikipedia.org/wiki/Newton%27s_method
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Newtons metod.
Wikimedia Commons har media som rör Newtons metod.
|































![{\displaystyle I=[a\;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8002af15630d9c7cd28558e7f48818dad3ade2c2)
![{\displaystyle I=]0\;\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec56e0eb96cb6ea2aeb25797c048fdedb4331284)