Planär graf

Exempel
Planär	Icke planär
Fjärilsgraf	Den kompletta grafen K₅
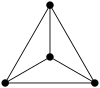Den kompletta grafen K₄	Den bipartita grafen K_3,3

Inom grafteori är en planär graf en graf som kan bäddas in i planet, det vill säga ritas på planet på ett sådant sätt att kanterna inte skär varandra, utan bara möts i noderna.^[1] En sådan avbildning kallas en plan graf eller planär inbäddning av grafen. En plan graf kan definieras som en planär graf med en avbildning av varje nod till en punkt i planet, och från varje kant till en plan kurva i planet, så att varje kurvas ändpunkter är de punkter som avbildas av kantens ändnoder och så att alla kurvor är disjunkta utom i ändpunkterna.

Varje graf som kan avbildas på ett plan kan avbildas på en sfär och vice versa.

En generalisering av planära grafer är grafer som kan ritas på en yta av ett givet genus. Med denna terminologi har planära grafer grafgenus 0, eftersom planet (och sfären) har genus 0.

Kuratowskis och Wagners satser[redigera | redigera wikitext]

Den polske matematikern Kazimierz Kuratowski bidrog med en karakterisering av planära grafer byggd på två förbjudna grafer, vilket nu är känt som Kuratowskis sats:

En ändlig graf är planär om och endast om den inte innehåller en delgraf som är en subdivision av K₅ (den kompletta grafen över fem noder) eller K_3,3 (den kompletta bipartita grafen över sex noder, så att tre av dem är förbundna med de andra tre).

En subdivision av en graf bildas om man sätter in noder i kanter (till exempel ändrar kanten •——• till •—•—•) noll eller flera gånger.

I stället för att betrakta subdivisioner behandlar Wagners sats minora av grafer:

En ändlig graf är planär om och endast om den inte har K₅ eller K_3,3 som en minor.

En minor bildas ur en graf genom kantkontraktion (att ta bort en kant genom att "smälta samman" dess två ändnoder).

En animation som visar att Petersengrafen innehåller en delgraf som är en minor, vilken är isomorf med K_3,3 (dessutom har Petersengrafen en även en minor som är isomorf med K₅ - smält samman 0 med 5, 1, med 6,..., 4 med 9).

Andra kriterier för planaritet[redigera | redigera wikitext]

I praktiken är det svårt att använda Kuratowskis kriterium för att snabbt avgöra om en graf är planär. Det finns dock snabba algoritmer för att lösa problemet: för en graf med n noder är det möjligt att avgöra i linjär tid O(n) huruvida en graf kan vara planär eller ej.

För en enkel sammanhängande planär graf med v noder och e kanter gäller följande enkla förhållanden:

Sats 1. Om v ≥ 3 så är e ≤ 3v − 6;

Sats 2. Om v ≥ 3 och det inte finns några cykler av längd 3, så är e ≤ 2v − 4.

I den här meningen är planära grafer glesa grafer eftersom de bara har O(v) kanter och blir asymptotiskt mindre än det maximala O(v²). Grafen K_3,3 har exempelvis sex noder och nio kanter och inga cykler av längd tre. Därför kan den enligt sats 2 inte vara planär. Märk att dessa satser ger nödvändiga, men inte tillräckliga, förutsättningar för planaritet och därför bara kan användas för att visa att en graf inte är planär. Om varken sats 1 eller 2 ger ett svar, får man använda andra metoder.

Eulers formel[redigera | redigera wikitext]

Huvudartikel: Eulerkarakteristik

Eulers formel säger att om en oändlig sammanhängande planär graf ritas i planet utan att några kanter skär varandra och v är antalet noder, e antalet kanter och f antalet "sidor" (områden begränsade av kanter, inklusive den oändligt stora ytan som omger grafen) så gäller

v − e + f = 2.

Som ett exempel kan vi ta fjärilsgrafen ovan: v = 5, e = 6 och f = 3. Detta gäller allmänt för alla planära grafer med f sidor, varje förändring av grafen som skapar en ny sida kommer inte att förändra v − e + f. Eftersom egenskapen gäller för alla grafer med f = 2, ger induktion att det gäller för alla andra fall. Eulers formel kan också visas enligt: Om grafen inte är ett träd, så avlägsna en kant som fullbordar en cykel. Detta sänker både e och f med ett och lämnar v − e + f konstant. Upprepa tills den kvarvarande grafen är ett träd. Träd har v = e + 1 och f = 1, vilket ger v − e + f = 2. Det vill säga Eulerkarakteristiken är 2.

I en ändlig, sammanhängande, enkel och planär graf avgränsas varje sida (utom möjligtvis den yttre) av minst tre kanter och varje kant vidrör högst två sidor. Genom att använda Eulers formel kan man visa att dessa är glesa i meningen att e ≤ 3v − 6 om v ≥ 3.

Eulers formel gäller också för konvexa polyedrar. Detta är ingen tillfällighet, eftersom varje konvex polyeder kan avbildas på en sammanhängande enkel planär graf medelst ett Schlegeldiagram - en avbildning ("projektion") av polyedern på ett plan med centrum valt nära centrum av en av polyederns sidor. Alla planära grafer motsvaras inte av en polyeder på detta sätt, exempelvis inte träd. Eulers formel gäller för alla polyedrar vars ytor är enkla polygoner som skapar en yta som är topologiskt ekvivalent med en sfär oavsett dess konvexitet.

Medelgrad[redigera | redigera wikitext]

Av v − e + f = 2 och $2e\geq 3f$ (en yta har minst tre kanter och varje kant har maximalt två ytor) följer att medelgraden är strikt mindre än sex. I annat fall kan en given graf inte vara planär.

Referenser[redigera | redigera wikitext]

^ Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication.). New York: Dover Pub. sid. 64. ISBN 978-0-486-67870-2. http://store.doverpublications.com/0486678709.html. Läst 8 augusti 2012. ”Thus a planar graph, when drawn on a flat surface, either has no edge-crossings or can be redrawn without them.”

[1] Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication.). New York: Dover Pub. sid. 64. ISBN 978-0-486-67870-2. http://store.doverpublications.com/0486678709.html. Läst 8 augusti 2012. ”Thus a planar graph, when drawn on a flat surface, either has no edge-crossings or can be redrawn without them.”

[1]