Elektriskt fält
| Den här artikeln behöver källhänvisningar för att kunna verifieras. (2018-12) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. |
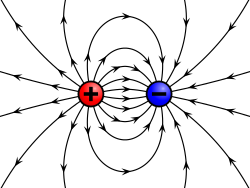
Ett elektriskt fält alstras av elektriskt laddade partiklar och tidsvarierande magnetfält. Det elektriska fältet beskriver den elektriska kraft som verkar på en orörlig positivt laddad testpartikel i varje punkt i rummet i förhållande till fältets källor (genererande elektriska laddningar). De första stegen mot den moderna behandlingen av det elektriska fältet togs av Michael Faraday.
Det elektriska fältet är ett vektorfält där fältvektorn (fältstyrkan) har SI-enheten newton per coulomb (N C-1), eller (helt ekvivalent) volt per meter (V m-1). Fältets riktning i en given punkt definieras som riktningen av den kraft som uppkommer på en positiv testladdning i punkten. Beloppet av fältet definieras som kvoten mellan kraftens belopp och laddningens storlek. Ett elektriskt fält innehåller elektrisk energi, med en energitäthet proportionell mot kvadraten på fältstyrkan.
En laddning i rörelse omger sig inte bara med ett elektriskt fält, utan även med ett magnetiskt fält och i en allmännare teori är dessa två fält inte längre separata entiteter – vad en observatör uppfattar som ett elektriskt fält kan en observatör i ett annat referenssystem uppfatta som en blandning av elektriska och magnetiska fält. Av denna anledning talar man inom fysiken ofta om ”elektromagnetism” och ”elektromagnetiska fält”. Inom kvantelektrodynamiken benämns det elektromagnetiska fältkvantat foton, en elementarpartikel med kvantiserad energi.
Definition (inom elektrostatiken)
[redigera | redigera wikitext]Det elektriska fältet definieras som elektrisk kraft per enhetsladdning
där är den elektriska kraften från Coulombs lag och q är den elektriska laddningen i den givna punkten.
Fältets riktning sammanfaller således med riktningen för kraften som fältet ger på en positiv punktladdning.
Denna ekvation är endast giltig i det elektrostatiska fallet, det vill säga när alla laddningar befinner sig i vila. I det mer generella fallet med laddningar i rörelse används istället Lorentz kraftlag.
Fältet från en punktladdning
[redigera | redigera wikitext]Det elektriska fältet runt en punktladdning är enligt Coulombs lag
där
- Q är laddningens storlek,
- r är avståndet från laddningen ("källpunkten") till den punkt där det elektriska fältet mäts ("fältpunkten"),
- är enhetsvektorn från källpunkten mot fältpunkten och
- är den elektriska konstanten.
Detta resultat går även att få från Gauss sats i det elektrostatiska fallet, vilken är en mer fundamental beskrivning av förhållandet mellan fördelningen av elektrisk laddning och det resulterande elektriska fältet. Gauss sats utgör i denna form en av Maxwells ekvationer, fyra fundamentala ekvationer inom elektromagnetismen.
Egenskaper (inom elektrostatiken)
[redigera | redigera wikitext]
Enligt ekvation (1) ovan är den elektriska fältstyrkan från en given punktladdning omvänt proportionell mot avståndet till laddningen i kvadrat.
Superpositionsprincipen gäller för elektriska fält. Det totala fältet i en punkt är vektorsumman av alla de enskilda fälten:
Om detta generaliseras till ett oändligt antal infinitesimala laddningselement fås
där
- är rymdladdningstätheten, mängden laddning per enhetsvolym.
Det elektrostatiska fältet är ett konservativt fält, något som inses genom
- Fältet från en punktladdning är konservativt
- En godtycklig laddningsfördelning kan delas upp i punktladdningar
- Användande av superpositionsprincipen
Detta innebär att det elektriska fältet kan skrivas som gradienten till en elektrisk potential
där är skalärfältet som beskriver den elektriska potentialen i en given punkt. Skillnaden i elektrisk potential mellan två punkter benämns vanligen elektrisk spänning.
Om ett flertal utbredda laddningar ger en sådan potential kan hessianen till den elektriska potentialen tolkas som en elektrisk fältgradient. Hessianen kommer att utgöra en symmetrisk tensor med spåret noll.
I ett medium med permittiviteten (som kan skilja sig ifrån - permittiviteten i vakuum), finns det ett (elektriskt) förskjutningsfält som är
Energi i det elektriska fältet
[redigera | redigera wikitext]Det elektriska fältet innehåller energi. Man kan visa att energitätheten i det elektriska fältet ges av
där
- är permittiviteten för det medium fältet befinner sig i
- är den elektriska fältvektorn
Den totala energin lagrad i ett elektrisk fält med volymen V är således
där
- är det differentiella volymselementet.
Paralleller mellan elektrostatik och mekanik
[redigera | redigera wikitext]- ,
vilken beskriver interaktionen mellan elektriska partiklar i vila, är lik Newtons gravitationslag:
Detta faktum pekar på likheter mellan det elektriska fältet och gravitationsfältet , något som lett till att analogier förekommer i undervisning och läroböcker.
Likheter mellan elektrostatiska och gravitationella krafter är till exempel
- Båda verkar även i vakuum
- Båda är centrala och konservativa
- Båda avtar med kvadraten på avståndet till källan
- Båda propagerar med en ändlig hastighet c
Skillnader mellan elektrostatiska och gravitationella krafter är exempelvis
- Elektrostatiska krafter är mycket större än gravitationella (med en faktor på ungefär 1036)
- Gravitationella krafter är alltid attraherande, men elektrostatiska kan vara antingen attraherande eller repulsiva (detta är anledningen till att gravitationen ”uppfattas” som en stark kraft)
- Gravitationella krafter är oberoende av medium, medan elektrostatiska krafter beror på mediet fältet befinner sig i. Detta beror på att materia innehåller laddningar – den snabba reaktionen från dessa till ett pålagt elektriskt fält ger upphov till ett sekundärt elektriskt fält som är så stort att man måste ta hänsyn till det. Den långsamma responsen hos en massa till ett växlande gravitationsfält gör att man oftast kan bortse från det sekundära fältet i detta fall, utom vid relativistiska hastigheter
Tidsvarierande elektriska fält (elektrodynamik)
[redigera | redigera wikitext]Laddningar i rörelse ger inte bara upphov till elektriska fält, utan även till magnetiska fält. Om dessa magnetiska fält varierar i tiden kommer de i sin tur att generera elektriska fält. Dessa kan beräknas med en av Maxwells ekvationer, den som ofta kallas Faradays induktionslag:
där
- är rotationen av det elektriska fältet och
- är tidsderivatan av det magnetiska fältet .
Detta innebär att ett tidsvarierande magnetiskt fält ger upphov till ett elektriskt virvelfält (som inte är ett konservativt fält). Tidsvarierande elektriska och magnetiska fält behandlas inom elektrodynamiken.
Se även
[redigera | redigera wikitext]Externa länkar
[redigera | redigera wikitext] Wikimedia Commons har media som rör Elektriskt fält.
Wikimedia Commons har media som rör Elektriskt fält.



























