Magnetfält
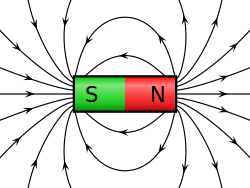
Magnetfält behandlas inom fysiken som vektorfält, vilka beskriver krafterna mellan magneter och strömförande elektriska ledare. Vektorfält kan åskådliggöras med hjälp av pilar av olika längd och riktning eller med fältlinjer, där fältstyrkan är proportionell mot linjetätheten. Magnetiska fält kan experimentellt synliggöras med hjälp av järnfilspån, vilka ställer in sig i fältlinjernas riktning.
Magnetiska fält produceras av rörliga elektriska laddningar och inneboende magnetiska moment hos elementarpartiklar, där momenten är associerade med en fundamental kvantmekanisk egenskap, deras spinn.[1][2]
Inom den speciella relativitetsteorin, är förhållandet mellan associerade elektriska och magnetiska fält beroende av den relativa hastigheten mellan observatör och elektriska laddningar.
Inom kvantfysiken är det elektromagnetiska fältet kvantiserat och växelverkan sker genom utbyten av fotoner.
Inledning[redigera | redigera wikitext]

Det magnetiska fältet kan definieras på flera ekvivalenta sätt beroende på hur det påverkar sin omgivning.
Fältet är ofta definierat genom den kraft det utövar på en rörlig laddad partikel. Det är känt från elektrostatiska experiment (orörliga laddningar) att en partikel med laddningen q i det elektriska fältet E påverkas med en kraft F = qE. Under andra omständigheter, som när en laddad partikel rör sig i närheten av en strömförande ledare, beror kraften också på partikelns hastighet. Den hastighetsberoende delen kan dock separeras ut så att kraften på partikeln uppfyller Lorentz kraftlag:
där v är partikelns hastighet och × betecknar kryssprodukten. Vektorn B benämns det magnetiska fältet och är definierad som det vektorfält som är nödvändigt för att Lorentz kraftlag korrekt skall beskriva en laddad partikels rörelse.
Alternativt, kan det magnetiska fältet beskrivas i termer av det vridmoment det orsakar på en magnetisk dipol.
Förutom B-fältet, finns ett annat fält, H-fältet, vilket också kallas magnetiskt fält. I vakuum är B och H proportionella där proportionalitetskonstanten endast beror på att olika enheter används. Inuti ett material är de dock olika.
B-fältet (magnetstyrka)[redigera | redigera wikitext]
| Benämningar för B[3] |
|---|
|
B-fältet, magnetstyrka, är ett av två sätt att betrakta magnetfält (det andra sättet är H-fältet). B-fältet mäts i SI-enheten tesla (T = Wb/m²) eller i cgs-enheten gauss (1 T = 10 000 Gauss). Tesla (T) är en förhållandevis stor enhet. Elektromagneter med järnkärna kan bara åstadkomma fält på någon tesla. Ofta använder man µT (mikrotesla, en miljondels tesla). Jordens magnetfält har styrkan 50 till 100 µT (0,5 gauss till 1 gauss).
Det magnetiska flödet (ofta betecknat med en stor grekisk bokstav fi Φ) mäts i Internationella måttenhetssystemet (SI) i Weber = volt·sekund.
Rörliga laddningar och B-fält (icke-relativistiska fallet)[redigera | redigera wikitext]

Det kanske enklaste exemplet på förekomsten av ett B-fält är det magnetiska fältet i omgivningen av en rak elektrisk ledare. Den danske fysikern Hans Christian Ørsted upptäckte att en magnetnål ställde in sig vinkelrätt mot en strömförande lednings riktning, vilket indikerade att magnetfält skapas av laddningar i rörelse.
Om en elektrisk laddning är i vila relativt en observatör, registrerar observatören endast ett elektriskt fält (elektrostatiska fallet). Om laddningen har en hastighet relativt observatören registrerar denne både ett elektriskt och ett magnetiskt fält. För en rörlig laddning förekommer B-fältet i riktningar skilda från partikelns rörelseriktning och är där riktat vinkelrätt mot E-fältet som är radiellt riktat från laddningen:
För punkten A kan det magnetiska fältet beräknas som
där v är partikelns hastighetsvektor, ur är riktningsvektorn till A och r är avståndet från laddningen till punkten A. Om vinkeln θ är noll är också B-fältet noll.
H-fältet (magnetiseringsstyrka)[redigera | redigera wikitext]
| Benämningar för H[3][4] |
|---|
|
H-fältet, magnetiseringsstyrka, är det andra sättet att betrakta magnetfält. H-fältet mäts i A/m och ses som orsakad av fria strömmar, medan B är orsakad av både elektriska strömmar och magnetiska ämnens magnetisering. I vakuum finns ingen magnetisering och därför gäller i SI
Värdet av den magnetiska konstanten μ0 (i vakuum lika med permeabiliteten μ) är genom Ampères lag en följd av enheten amperes definition.
Fältstyrkor[redigera | redigera wikitext]
Den precision som kan uppnås med Gravity Probe B-experiment är 5 attotesla (5 10-18 T). [5]
Det starkaste magnetfältet producerat i ett laboratorium är 2.8 kT (VNIIEF, Sarov, Ryssland, 1998).[6] Den magnetiseringsstyrkan för vissa astronomiska objekt sådana som magnetarer är mycket högre; magnetarer varierar mellan 0.1 och 100 GT (108-1011 T).[7]
Magnetiska fältmodeller[redigera | redigera wikitext]
Magnetfält kan beräknas enbart med hjälp av B-fält (vissa läroböcker behandlar inte H-fältet överhuvudtaget), vilket på ett jämförelsevis enkelt sätt låter sig göras i frånvaro av magnetiserbara material. Om magnetiska/magnetiserbara kroppar är närvarande uppstår av praktiska skäl ett behov av modeller för att i makroskopisk skala behandla dessa kroppar. Att enbart begagna sig av B-fältet innebär till exempel svårigheter att ställa upp ekvationer för att bestämma området som bildar övergången mellan den magnetiska kroppen och resten av fältet. Om den magnetiska/magnetiserbara kroppen i sin tur är sammansatt av magnetiska domäner av olika former och storlekar kan fältberäkningar bli praktiskt taget omöjliga att genomföra.
H-fältet och gilbertmodellen[redigera | redigera wikitext]

Det är ibland användbart att modellera kraften och vridmomentet mellan två magneter som på grund av magnetiska poler repellera eller attrahera varandra, på samma sätt som coulombkraften mellan elektriska laddningar. Detta kallas gilbertmodellen för magnetism, efter William Gilbert. I denna modell produceras ett magnetiskt H-fält av magnetiska laddningar som är "utsmetade" runt varje pol. H-fältet är således analog till det elektriska fältet E, som börjar vid en positiv elektrisk laddning och slutar på en negativ elektrisk laddning. Nära nordpolen pekar därför alla H-fältlinjer bort från nordpolen (vare sig inne i magneten eller utanför), medan nära sydpolen (vare sig inne i magneten eller utanför) pekar alla H-fältlinjer mot sydpolen. En nordpol, känner en kraft i riktningen för H-fältet medan kraften på en sydpol är motsatt H-fältets riktning.
I den magnetiska polmodellen är den elementära magnetiska dipolen m bildad av två motsatta magnetiska poler av styrkan qm och separerade av en mycket liten avståndsvektor d, så att m = qmd.
Eftersom modellen är baserad på den fiktiva idén om en "magnetisk laddningsdensitet", har gilbertmodellen begränsningar. De magnetiska polerna kan inte existera åtskilda från varandra som elektriska laddningar kan och måste alltid komma i nord/syd par. Om ett magnetiserat objekt delas upp i två halvor, kommer en ny pol att uppträda på ytan av varje del, så var och en kommer att ha ett par av komplementära poler. Den magnetiska polmodellen tar inte hänsyn till magnetism som produceras av elektriska strömmar och ger endast rätt magnetfält utanför magnetiska material.
Amperska kretsmodellen och B-fältet[redigera | redigera wikitext]

Efter Örsteds upptäckt att en elektrisk ström skapar ett magnetfält och Amperes upptäckt att elektriska strömmar attraherar och repellerar varandra likt magneter, var det naturligt att anta att alla magnetiska fält beror på elektriska strömslingor. I denna modell som utvecklats av Ampere är den elementära magnetiska dipol som orsakar magneterna en tillräckligt liten ampersk slinga med strömstyrkan I. Dipolmomentet för denna krets är m = IA där A är ett område av slingan.
Dessa magnetiska dipoler producerar ett magnetiskt B-fält. En viktig egenskap hos B-fältet som produceras på detta sätt är att magnetiska B-fältlinjer varken har start- eller slutpunkt (B är ett solenoidalt fält); en fältlinje antingen sträcker sig till oändligheten eller sveper runt för att bilda en sluten kurva.
Magnetiska fältlinjer kan också lindas runt, runt utan att slutas, men också utan att upphöra. Dessa mer komplicerade icke-slutna icke-ändliga magnetiska fältlinjer är omtvistade, trots att det magnetiska fältet av föremål som producerar dem, beräknas genom att addera de magnetiska områdenas "elementära delar" vars magnetiska fältlinjer verkligen har formen av slutna kurvor eller är förlängda till oändligheten. Hittills har inget undantag från denna regel hittats. Magnetiska fältlinjer lämnar en magnet nära dess nordpol och tränger in nära dess sydpol, men inne i magneten fortsätter B-fältlinjerna genom magneten från sydpolen till nordpolen. För att inse att detta måste vara sant kan man föreställa sig att placera en kompass inuti en magnet. Om kompassen är nära en B-nordpol pekar den mot denna nordpol eftersom magneter staplade på varandra pekar i samma riktning - fältlinjen som går in i en magnet någonstans måste lämna magneten någon annanstans; det är inte tillåtet att ha en ändpunkt. Magnetiska poler måste därför alltid komma i par av N och S.
Mera formellt, alla magnetiska fältlinjer som kommer in i en region måste också lämna regionen. De magnetiska fältlinjerna är i första hand ett konceptuellt verktyg som används för att representera matematiken bakom beräkningar av magnetfält. Det totala "antalet" fältlinjer är beroende av hur fältlinjerna dras. I praktiken är det integralekvationer som den nedan, som används. Antalet fältlinjer som kommer in i regionen minus det antal som lämnar är noll. Matematiskt motsvarar detta:
där integralen är en ytintegral över den slutna ytan S (en sluten yta omger ett område helt). Eftersom dA pekar utåt, är skalärprodukten i integranden positiv då B-fältet pekar ut från ytan och negativ då B-fältet pekar in.
Magnetisering[redigera | redigera wikitext]

Det finns inom SI två sätt att hantera magnetiska fält orsakade av material. Enligt det ena sättet betraktas ämnets magnetisering som orsakad av hypotetiska amperska strömmar (i motsats till fria strömmar). Då får man
där
- [3]
Magnetiseringens vektorfält M anger hur starkt en region av ett material magnetiseras. Det definieras som nettot av magnetiska dipolmoment per volymenhet för denna region. Magnetiseringen av en likformig magnet, är därför en konstant för materialet som är lika med dess magnetiska moment, m, dividerat med dess volym. Eftersom SI-enheten för magnetiska moment är A m2 är SI-enheten för magnetiseringen M A/m, identisk med den för H-fältet.
När magnetiseringen betraktas som proportionell mot de fria strömmarnas fält, kan man skriva
- ,
där μr är ämnets relativa magnetiska permeabilitet. I mjuka ferromagnetiska material kan μr vara av storleksordningen 10³ eller större. I paramagnetiska och diamagnetiska material är magnetiseringen liten. Där brukar man räkna med magnetisk susceptibilitet χ där M = χ H, så att μr = 1 + χ. Diamagnetiska ämnens susceptibilitet är negativ, av storleksordningen -10-6. Även i paramagnetiska material är χ liten, men positiv.
Det andra sättet räknar med storheten intensitet av magnetisering, betecknad med vektorfältet I. Här gäller
Man ser att I har enheten tesla. Det här sättet är vanligt när man beskriver ferromagnetiska material, där mättnadsmagnetisering ofta ges i tesla. Så har till exempel järn en maximal magnetiseringsintensitet på 2,1 T.
Materialegenskaper[redigera | redigera wikitext]

De flesta material reagerar på ett pålagt B-fält genom att producera en egen magnetisering M och därmed ett eget B-fält. Vanligtvis är reaktionen mycket svag och existerar bara så länge det finns ett yttre magnetfält. Termen magnetism syftar på en beskrivning av hur material reagerar på mikroskopisk nivå på ett yttre magnetiskt fält och termen används för att kategorisera ett materials magnetiska tillstånd. Material indelas i grupper grundade på deras magnetiska egenskaper:
- Diamagnetiska material[8] orsakar en magnetisering som verkar i motsatt riktning gentemot det pålagda fältet
- Paramagnetiska material[8] orsakar en magnetisering vars fältriktning är den samma som det pålagda fältet
- Ferromagnetiska material och antiferromagnetiska material[9][10] kan ha en magnetisering som är oberoende av det pålagda B-fältet och med en komplex relation mellan de två fälten
- Supraledande material [11][12] kännetecknas av en ideal ledningsförmåga under en kritisk temperatur och magnetstyrka. De är i hög grad magnetiska och kan bilda perfekta diamagneter.
I fallet paramagnetism och diamagnetism, är magnetiseringen M ofta proportionell mot det pålagda magnetiska fältet:
där μ är den materialberoende permeabiliteten.
Magnetiska vridmoment[redigera | redigera wikitext]

Om två lika poler av två separata magneter är nära varandra och en av magneterna är vridbar, roterar den för att anpassa sig till den första. I detta exempel, skapar det magnetiska fältet hos den stationära magneten ett magnetiskt moment på magneten som är fri att rotera. Detta magnetiska moment τ tenderar att inrikta en magnets poler i linje med den magnetiska fältriktningen. En kompassnål roterar för att få samma riktning som jordens magnetfält.
Magnetiska vridmoment används för att driva elektriska motorer. I en enkel motorkonstruktion, är en magnet fastsatt på en fritt roterande axel och utsätts för ett magnetiskt fält från ett antal elektromagneter. Genom att i en viss takt kasta om den elektriska strömmens riktning genom var och en av elektromagneterna och därmed vända polariteten för deras magnetiska fält, bildas ett roterande magnetiskt fält sett från rotorn (den roterande delen). Ett vridmoment uppstår vars storlek beror av skillnaden i varvtal mellan magnetfält och rotor (rotorn strävar att anta samma varvtal som fältet).
Liksom är fallet för kraften mellan magneterna, leder den magnetiska polmodellen till rätt ekvation. Antag att två lika och motsatta magnetiska laddningar påverkas av samma H-fält med lika och motsatta krafter, vilka ger ett vridmoment proportionellt mot avståndet (räknat vinkelrätt mot H-linjerna) mellan polerna (se bild). Om förbindningslinjen mellan polerna bildar vinkeln θ med H-linjerna och avståndet mellan polerna är d, är det momentana vridmomentet
där μ0 är permeabiliteten för vakuum, 4π × 10-7 Vs/(Am).
Den amperska modellen med kretsande strömmar förutsäger samma magnetiska moment. Här är det B-fältet som växelverkar med den amperska strömslingan genom en lorentzkraft. Resultaten är desamma även om modellerna är helt annorlunda.
Vridmomentet τ på en liten magnet är proportionellt både mot den magnetstyrkan och det magnetiska momentet m:
där × representerar kryssprodukten.
Energi lagrad i magnetiska fält[redigera | redigera wikitext]
Energi behövs för att alstra ett magnetfält både för att arbeta mot det elektriska fält ett föränderligt magnetfält skapar och att ändra magnetiseringen av vilket material som helst inom det magnetiska fältet. För dispersiva material frigörs denna energi när magnetfältet avlägsnas och denna energi kan därför modelleras som lagrad i magnetfältet.
För linjära, icke-dispersiva material (sådana att B = μH där μ är frekvensoberoende), är energidensiteten
Saknas omgivande magnetiska material kan μ ersättas med μ0. Ekvationen kan inte användas för icke-linjära material, utan en mer generell formulering enligt nedan, måste användas.
I allmänhet kan den inkrementella mängden arbete per enhetsvolym som är nödvändig för att orsaka en liten ändring i det magnetiska fältet skrivas
När relationen mellan H och B är känd, kan denna ekvation användas för att bestämma det arbete som är nödvändigt för att uppnå ett visst magnetiseringstillstånd. Om hysteresis, som för ferromagneter och supraledare, förekommer beror arbetet också på hur det magnetiska fältet skapas.
Förening med elektriskt fält[redigera | redigera wikitext]

Ørsted, Faraday och Maxwell visade experimentellt och teoretiskt att magnetiska och elektriska fält betingar varandra och kan beskrivas av det elektromagnetiska fältet som är en förening av de magnetiska och elektriska fälten. Elektromagnetisk strålning kan behandlas inom ramen för detta elektromagnetiska fält.
Albert Einsteins arbete i form av den speciella relativitetsteorin ledde till att de magnetiska och elektriska fälten kunde beskrivas av ett elektromagnetiskt tensorfält som är invariant under Lorentztransformationen. Detta innebär bland annat att medan de elektriska och magnetiska fältkomponenterna kan variera mellan olika inertialsystem är den totala Lorentzkraften som verkar på en viss laddning invariant under dessa transformationer. Detta kan anses vara det andra steget i föreningen av de magnetiska och elektriska fälten.
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ Jiles, David C. (1998). Introduction to Magnetism and Magnetic Materials (2). CRC. Sid. 3. ISBN 0412798603. http://books.google.com/books?id=axyWXjsdorMC&pg=PA3&dq=#v=onepage&q&f=false.
- ^ Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew (1964). The Feynman Lectures on Physics. "2". California Institute of Technology. Sid. 1.7-1.8. ISBN 0465079989. http://books.google.com/books?id=uaQfAQAAQBAJ&printsec=frontcover&dq=%22magnetic+field.
- ^ [a b] Electromagnetics, by Rothwell and Cloud, p23
- ^ R.P. Feynman, R.B. Leighton, M. Sands (1963). The Feynman Lectures on Physics, volume 2.
- ^ ”Gravity Probe B Executive Summary”. sid. 10, 21. Arkiverad från originalet den 9 oktober 2022. https://ghostarchive.org/archive/20221009/http://www.nasa.gov/pdf/168808main_gp-b_pfar_cvr-pref-execsum.pdf. Läst 20 september 2014.
- ^ ”With record magnetic fields to the 21st Century”. IEEE Xplore. http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=823621.
- ^ Kouveliotou, C.; Duncan, R. C.; Thompson, C. (February 2003). "Magnetars Arkiverad 11 juni 2007 hämtat från the Wayback Machine.". Scientific American; Page 36.
- ^ [a b] RJD Tilley (2004). Understanding Solids. Wiley. Sid. 368. ISBN 0-470-85275-5. http://books.google.com/?id=ZVgOLCXNoMoC&pg=PA368.
- ^ Sōshin Chikazumi, Chad D. Graham (1997). Physics of ferromagnetism (2). Oxford University Press. Sid. 118. ISBN 0-19-851776-9. http://books.google.com/?id=AZVfuxXF2GsC&printsec=frontcover.
- ^ Amikam Aharoni (2000). Introduction to the theory of ferromagnetism (2). Oxford University Press. Sid. 27. ISBN 0-19-850808-5. http://books.google.com/?id=9RvNuIDh0qMC&pg=PA27.
- ^ M Brian Maple et al. (2008). ”Unconventional superconductivity in novel materials”. i K. H. Bennemann, John B. Ketterson. Superconductivity. Springer. Sid. 640. ISBN 3-540-73252-7. http://books.google.com/?id=PguAgEQTiQwC&pg=PA640.
- ^ Naoum Karchev (2003). ”Itinerant ferromagnetism and superconductivity”. i Paul S. Lewis, D. Di (CON) Castro. Superconductivity research at the leading edge. Nova Publishers. Sid. 169. ISBN 1-59033-861-8. http://books.google.com/?id=3AFo_yxBkD0C&pg=PA169.
Allmänna källor[redigera | redigera wikitext]
- Jackson 1975, chapter 5
- Nayfeh & Brussel 1985, chapter 9
- "Units for Magnetic Properties". Lake Shore Cryotronics, Inc. Retrieved 2009-10-24.
Vidare läsning[redigera | redigera wikitext]
- Jackson, John David (1975). Classical Electrodynamics (Second ed.). John Wiley & Sons. ISBN 0-471-43132-X.
- Nayfeh, Munir H.; Brussel, Morton K. (1985). Electricity and Magnetism. John Wiley & Sons. ISBN 0-471-87681-X.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör magnetfält.
Wikimedia Commons har media som rör magnetfält.
| |||||||||||||
|















