Hubbles lag
Hubbles lag beskriver observationen inom fysikalisk kosmologi att hastigheten med vilken olika galaxer avlägsnar sig bort från oss är proportionell mot deras avstånd från jorden. "Lagen" är en teori från 1929 uppkallad efter astronomen Edwin Hubble från USA. Då han hade märkt att galaxerna rör sig från varandra, slöt han sig till att universum expanderar. I själva verket expanderar rum-tid volymen av det observerbara universumet och Hubbles lag är direkta fysiska observationer av denna process.[1] Det är den första observerbara grunden för universums expansion och idag fungerar som ett delbevis som oftast nämns som stöd för big bang-teorin.
Även om lagen allmänt tillskrivs Edwin Hubble, var lagen först härledd från den allmänna relativitetsteorins ekvationer av den belgiske astronomen och prästen Georges Lemaître i en artikel år 1927 där han föreslog att universum expanderar och beräknade värdet på utvidgningen, som nu kallas Hubblekonstanten med mätdata från Vesto Slipher och Edwin Hubble.[2][3][4][5][6][7] Två år senare bekräftade Edwin Hubble förekomsten av denna lag och fastställde ett mer noggrant värde för den konstant som nu bär hans namn.[8] Innebörden var att objektens fjärmandehastighet var orsaken till deras rödförskjutningar, många tidigare mätta av den amerikanske astronomen Vesto Slipher år 1917 och relaterade till hastighet av honom.[9]
Galaxerna avlägsnar sig från varandra med en hastighet proportionell mot avståndet mellan galaxer och lagen uttrycks av ekvationen:
där är en konstant som kallas Hubblekonstanten. Hubbleparametern är en parameter och en funktion av tiden. Dess nuvarande värde betecknas . Avståndet eller mer specifikt egenavståndet (eng. proper distance) till en galax som kan ändras med tiden (till skillnad från medflyttande avstånd (eng. comoving distance)) och dess hastighet (dvs. derivatan av egenavståndet med avseende på kosmologisk tidskoordinat.[10] SI-enheten för är s −1 men den är oftast angiven i (km/s)/Mpc, vilket ger hastigheten i km/s för en galax med avstånd på 1 megaparsec.
Upptäcktshistorik[redigera | redigera wikitext]
Ett decennium innan Hubble gjorde sina observationer hade ett antal fysiker och matematiker etablerat en konsistent teori om sambandet mellan rum och tid genom att använda Einsteins fältekvationer från den allmänna relativitetsteorin. Genom att tillämpa de mest generella principerna på universum fick man en dynamisk lösning som stred mot den då förhärskande uppfattningen om ett statiskt universum.
FLRW ekvationer[redigera | redigera wikitext]
År 1922 härledde den ryske matematikern och kosmologen Aleksandr Fridman (ty. Alexander Friedmann) sina Friedmanns ekvationer från Einsteins fältekvationer, som visar att universum kan expandera med en hastighet som kan beräknas med hjälp ekvationerna.[11] Parametern, som används av Friedmann, är känd idag som den kosmiska skalfaktorn, som kan ses som en skalinvariant form av proportionalitetskonstanten i Hubbles lag. Georges Lemaître härledde oberoende av Friedman en liknande lösning år 1927. Friedmanns ekvationer härleds genom att infoga Friedmann-Lemaître-Robertsson-Walker (FLRW)-metriken för ett homogent och isotropt universum i Einsteins fältekvationer för en fluid med en given densitet och ett givet tryck. Idén om en expansion av rum-tiden skulle så småningom leda till steady state-teorin och big bang-teorin inom kosmologin.
Universums form[redigera | redigera wikitext]
Före tillkomsten av modern kosmologi, fanns en betydande diskussion om universums storlek och form. År 1920 ägde den uppmärksammade Shapley-Curtisdebatten rum mellan amerikanerna Harlow Shapley och Heber Curtis i denna fråga. Shapley argumenterade för ett litet universum med storleken av Vintergatan och Curtis hävdade att universum var mycket större. Problemet löstes under det följande årtiondet med Hubbles förbättrade observationer.
Cepheid-stjärnor utanför Vintergatan[redigera | redigera wikitext]
Edwin Hubble gjorde det mesta av sitt professionella astronomiska observerande arbete vid Mount Wilson-observatoriet i Kalifornien, världens då mest kraftfulla teleskop. Hans observationer av Cepheid-stjärnor i spiralnebulosor gjorde att han, baserat på en grundteori utarbetad av Henrietta Swan Leavitt,[12] kunde beräkna avstånd till dessa. Dessa objekt upptäcktes överraskande ligga på ett avstånd som placerade dem väl utanför Vintergatan. De fortsatte att kallas "nebulosor" och det var bara gradvis som termen "galaxer" tog över.
Kombinera rödförskjutningar med avståndsmätningar[redigera | redigera wikitext]
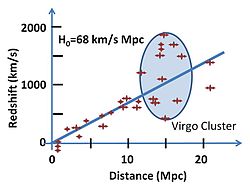
De parametrar som ingår i Hubbles lag, hastigheter och avstånd, mäts inte direkt. I verkligheten bestäms, till exempel en supernovas ljusstyrka, som ger information om supernovans avstånd och rödförskjutningen z = ∆λ/λ i dess strålningsspektrum. Hubble korrelerade ljusstyrka och parametern z.
Genom att kombinera sina mätningar av galaxavstånd med Vesto Sliphers och Milton Humasons mätningar av rödförskjutningar knutna till galaxerna, upptäckte Hubble en ungefärlig proportionalitet mellan rödförskjutningen hos ett objekt och dess avstånd även om det var betydande spridning (enligt dagens kunskap orsakat av särhastighet (eng. peculiar velocity). Hubbleflödet används att referera till den fjärmande rörelse i den region i rymden som är tillräckligt långt ut så att fjärmandehastigheten (eng. recession velocity) är större än lokal ”särhastighet”. Hubble kunde rita en trendlinje med de 46 galaxer han studerade och få ett värde på Hubblekonstanten på 500 (km/s)/Mpc (mycket högre än dagens accepterade värden på grund av fel i hans avståndskalibreringar). (Se kosmisk avståndsstege för detaljer.)
Vid tiden för upptäckt och utveckling av Hubbles lag var det acceptabelt att förklara rödförskjutningsfenomenet som en dopplereffekt i sammanhang med speciella relativitetsteorin och använda formeln för dopplereffekt för att associera rödförskjutning z med hastighet. Idag ses hastighet-avståndsförhållandet i Hubbles lag som ett teoretiskt resultat med hastighet vara kopplad till observerad rödförskjutning och inte genom dopplereffekten utan genom en kosmologisk modell relaterande fjärmandehastighet till universums expansion. Även för små z tolkas hastigheten i Hubbles lag inte längre som en dopplereffekt, även om för små z är hastighet-rödförskjutning sambandet detsamma för båda förklaringssätten.
År 1958 publicerades den första bra beräkningen av H0, 75 (km/s)/Mpc, av Allan Sandage.[13] Men det skulle ta flera årtionden innan samstämmighet uppnåddes.
Hubblediagram[redigera | redigera wikitext]
Hubbles lag kan lätt grafiskt återgivas i ett Hubblediagram i vilket hastigheten (förmodat ungefär proportionell mot rödförskjutningen) hos ett objekt ritas som en funktion av dess avstånd till observatören.[14] En rät linje med en positiv lutning i det här diagrammet är den grafiska bilden av Hubbles lag.
Kosmologiska konstanten övergiven[redigera | redigera wikitext]
Efter att Hubbles upptäckt publicerats tog Albert Einstein avstånd från sitt arbete med den kosmologiska konstanten, som han hade lagt till för att modifiera sina ekvationer i allmänna relativitetsteorin, för att låta dem att ge en statisk lösning. Något som hans ekvationer inte tillät så som de ursprungligen var utformade. Han kallade senare detta arbete sitt "största misstag" eftersom det var ett felaktigt antagande med ett statiskt universum, vilket hade orsakat honom att inte godta vad kan ses i hans ekvationer i den allmänna relativitetsteorin: faktumet att den allmänna relativitetsteorin både förutsåg och gav möjlighet att beräkna universums expansion, som (liksom krökning av ljus under inverkan av gravitationen vid stora massor eller precessionen av Merkurius omloppsbana) experimentellt kunde observeras och jämföras med hans teoretiska beräkningar med hjälp av särskilda lösningar på allmänna relativitetsteorins ekvationer så som han hade ursprungligen formulerade dem.
Einstein gjorde en resa till Mount Wilson år 1931 för att tacka Hubble för att ha tagit fram den observationella grunden för modern kosmologi.[15]
Den kosmologiska konstanten har åter fått aktualitet under de senaste decennierna som en hypotes för mörk energi.[16]
Utläggning[redigera | redigera wikitext]
Upptäckten av det linjära förhållandet mellan rödförskjutning och avstånd, tillsammans med ett förmodat linjärt förhållande mellan fjärmande hastighet och rödförskjutning, ger ett enkelt matematiskt uttryck för Hubbles lag enligt följande:
där
- är fjärmande hastigheten, vanligen uttryckt i km/s.
- är Hubblekonstanten och motsvarar värdet av H (ofta kallas den Hubbleparametern som har ett värde som är tidsberoende och som kan uttryckas i form av skalfaktorn) i Friedmanns ekvationer taget vid tiden för observation betecknad med index 0. Detta värde är densamma i hela universum för en viss medflyttande tid (eng. comoving time).
- är avståndet (eller egenavståndet (eng. proper distance), som kan ändras över tiden, (till skillnad från medflyttande avstånd (eng. comoving distance) som är konstant) från galaxen till observatören, mätt i megaparsec (Mpc), i den tredimensionella rymden fastställd vid given kosmologisk tid. (Den fjärmande hastigheten är v = dr/dt).
Hubbles lag anses vara ett grundläggande samband mellan fjärmande hastighet och avstånd. Sambandet mellan fjärmande hastighet och rödförskjutning beror på den kosmologiska modell som antagits, men är inte säkerställt utom för små rödförskjutningar.
För avstånd större än radien i en Hubblesfär fjärmar sig objekt snabbare än ljusets hastighet:
Eftersom Hubblekonstanten är en konstant endast i rummet, inte i tiden, kan radien i Hubblesfären öka eller minska under olika tidsintervall. Indexet 0 anger det nuvarande värdet på Hubblekonstanten.[18] Aktuell forskning visar att universums expansion accelererar (se avsnittet Acceleration av expansionen), vilket innebär att för varje given galax, den fjärmande hastigheten dr/dt ökar över tiden samtidigt som galaxen avlägsnar sig till större och större avstånd. Hubbleparametern tros dock faktiskt minska med tiden, vilket betyder att om vi skulle titta på något fast avstånd r och titta på en serie olika galaxer passera detta avstånd, senare galaxer skulle gå denna sträcka med en mindre hastighet än de tidigare galaxerna.[19]
Rödförskjutningshastighet och fjärmande hastighet[redigera | redigera wikitext]
Rödförskjutning kan mätas genom att bestämma våglängden för en känd spektrallinje, såsom vätets α-linjer för avlägsna kvasarer, och mäta dess förskjutning jämfört med en stationär referens. Rödförskjutning är således en storhet som entydigt kan observeras experimentellt. Sambandet mellan rödförskjutning och fjärmande hastighet är en annan sak. För en omfattande diskussion se Harrison.[20]
Rödförskjutningshastighet[redigera | redigera wikitext]
Rödförskjutning beskrivs ofta som en rödförskjutningshastighet, som är den fjärmande hastighet som skulle ge samma rödförskjutning om den var orsakad av en linjär dopplereffekt (vilket dock inte är fallet, då förskjutningen delvis orsakas av en kosmisk expansion av rymden, och eftersom de inblandade hastigheterna är för stora för att använda en icke-relativistisk formel för dopplereffekt). Denna rödförskjutningshastighet kan lätt överstiga ljusets hastighet.[21] Med andra ord, för att bestämma rödförskjutningshastigheten , används uttrycket:[22][23]
Det är ingen grundläggande skillnad mellan rödförskjutningshastighet och rödförskjutning. De är helt proportionella, och inte relaterade genom något teoretiskt resonemang. Motiveringen bakom terminologin "rödförskjutningshastighet" är att rödförskjutningshastighet stämmer med hastigheten vid en-låg-hastighets förenkling av den så kallade relativistiska dopplereffekten.[24]
Här är och den observerade respektive emitterade våglängden. "Rödförskjutningshastigheten" är inte lika enkelt relaterad till verklig hastighet vid högre hastigheter och denna terminologi leder till förvirring om den tolkas som en verklig hastighet. I det följande diskuteras kopplingen mellan rödförskjutning eller rödförskjutningshastighet och fjärmande hastighet. Denna diskussion är baserad på Sartori.[25]
Fjärmande hastighet[redigera | redigera wikitext]
Antag att är universums skalfaktor och ökar när universum expanderar på ett sätt som beror på vald kosmologisk modell. Dess innebörd är att alla mätta avstånd mellan medflyttande (eng. comoving) punkter ökar proportionellt mot . (De medflyttande punkterna rör sig inte i förhållande till varandra utom genom expansion av rymden.) Med andra ord:
där är någon vald referenstid. Om ljus skulle emitteras från en galax vid tiden och tas emot av oss vid , är det rödförskjutet på grund av universums expansion, och denna rödförskjutning z är helt enkelt:
Antag att en galax finns på ett avstånd och detta avstånd ändras med tiden i en takt av . Vi kallar denna takt av fjärmande för den fjärmande hastigheten (eng. recession velosity) :
Vi definierar nu Hubblekonstanten som
och får Hubbles lag:
Ur detta perspektiv är Hubbles lag ett grundläggande samband mellan (i) fjärmande hastigheten orsakad av rymdens expansion och (ii) avståndet till ett objekt. Kopplingen mellan rödförskjutning och avstånd är ett stöd som används för att koppla Hubbles lag till observationer. Denna lag kan approximativt relateras till rödförskjutningen genom att göra en expansion av en Taylorserie:
Om avståndet inte är alltför stort, blir alla andra komplikationer av modellen små korrigeringar och tidsintervallet är helt enkelt avståndet dividerat med ljushastigheten:
- eller
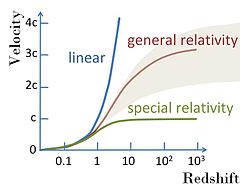
Enligt denna ansats är uttrycket en approximation giltigt vid små rödförskjutningar, för att ersättas av ett annat uttryck vid stora rödförskjutningar vilket är beroende av vald modell. Se figur Velocity-Redshift.
Observerbarhet av parametrar[redigera | redigera wikitext]
Strängt taget är varken eller i formeln direkt observerbara, eftersom de är egenskaper i nutid hos en galax, medan våra observationer är från galaxen i en förfluten tid, vid den tidpunkt som ljuset, som vi nu ser, lämnade galaxen.
För relativt närliggande galaxer (rödförskjutningen är mycket mindre än ett) kommer och inte har ändrats mycket och kan uppskattas med hjälp av formeln där är ljusets hastighet. Detta ger det empiriska uttrycket som hittades av Hubble.
För avlägsna galaxer kan inte (eller ) beräknas från utan att ange en detaljerad modell för hur ändras med tiden. Rödförskjutningen är inte ens direkt relaterad till fjärmande hastigheten vid den tid när ljuset emitterades, men det finns en enkel tolkning: är den faktor med vilken universum expanderat medan fotonen färdats mot observatören.
Expansionshastighet vs. relativ hastighet[redigera | redigera wikitext]
När Hubbles lag används för att bestämma avstånd, kan endast hastigheten på universums expansion användas. Då genom gravitation samverkande galaxer rör sig i förhållande till varandra oberoende av universums expansion, dessa relativa hastigheter kallas särhastigheter (eng. peculiar velocities), måste hänsyn tas till detta vid användning av Hubbles lag.
Om hög särhastighet existerar bland galaxhopar visar den sig som utsträckt distorsion av rödförskjutningen i radiell riktning. Denna rödförskjutningseffekt (eng. Finger of God effect) upptäckt 1938 av Benjamin Kenneally, är ett resultat av ovan fenomen. I system som är sammanhållna av gravitationen, såsom galaxer eller vårt planetsystem, är rymdens expansion en mycket svagare effekt än den sammanhållande gravitationskraften.
Idealiserad Hubbles lag[redigera | redigera wikitext]
Den matematiska härledningen av en idealiserad Hubbles lag för ett uniformt expanderande universum är en ganska elementär geometrisk uppställning i ett tredimensionellt kartesiskt/newtonskt koordinatrum, som betraktas som ett metriskt rum, är helt homogent och isotropt (egenskaper varierar inte med läge eller riktning). Enkelt uttryckt är teoremet detta:
- Vilka som helst av två punkter som rör sig bort från ursprunget, var och en i sin egen raka riktning och med en hastighet som är proportionell mot avståndet från ursprunget, kommer att röra sig från varandra med en hastighet som är proportionell mot avståndet mellan dem.
I själva verket gäller detta för icke-kartesiska rum så länge de är lokalt homogena och isotropa; särskilt för de negativt och positivt krökta rummen ofta studerade som kosmologiska modeller (se form på universum).
En iakttagelse som härrör från detta teorem är, att objekt som fjärmar sig från jorden inte är en indikation på att jorden är nära ett centrum från vilket utvidgningen sker, utan snarare att alla observatörer i ett expanderande universum skulle se objekt fjärma sig från dem.
Universums ålder och framtid[redigera | redigera wikitext]
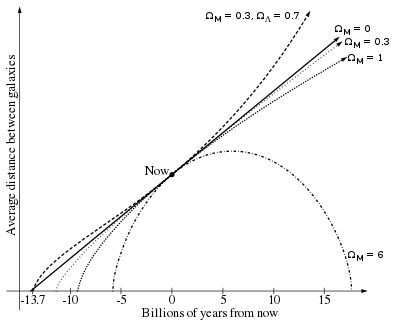
Värdet på Hubbleparametern ändras över tiden antingen ökas eller minskas beroende på tecknet på parametern för den så kallade kosmiska decelerationsparametern som definieras av
I ett universum med en decelerationsparameter lika med noll, följer det att , där är tiden från big bang. Ett icke-noll, tidsberoende värde på kräver helt enkelt integration av Friedmanns ekvationer bakåt från nutid till den tid då storleken på vårt observerbara universums horisont var noll.
Länge trodde man att var positiv, som indikerar att utvidgningen saktar ned på grund av gravitationskraft. Detta skulle innebära en ålder på universum som är mindre än (som är ca 14 miljarder år). Till exempel ett värde på på 1/2 (en gång förordat av de flesta teoretiker) skulle ge en ålder på universum på ). Upptäckten år 1998 att är uppenbarligen negativ innebär att universum faktiskt kunde vara äldre än . Beräkningar av universums ålder ligger dock mycket nära .
Olbers paradox[redigera | redigera wikitext]
Universums expansion sammanfattad av big bang uttydningen av Hubbles lag är relevant för den gamla frågeställningen kallad Olbers paradox: om universum var oändligt, statiskt och fyllt med en jämn fördelning av stjärnor, då skulle synlinjen i alla riktningar på himlen sluta på en stjärna, och himlen skulle vara lika ljus som ytan på en stjärna. Natthimlen är dock till största delen mörk. Sedan 1600-talet har astronomer och andra tänkare föreslagit många möjliga lösningar på denna paradox, men den för närvarande accepterade lösningen beror delvis på big bang-teorin och delvis på Hubbles lag. I ett universum, som finns under en ändlig tid, har endast ljuset från ett begränsat antal stjärnor haft en möjlighet att nå oss, och paradoxen finns inte. Dessutom i ett expanderande universum avlägsnar sig fjärran objekt från oss, vilket leder till att ljuset från dem rödförskjuts och minskar i ljusstyrka.[26]
Dimensionslösa Hubbleparametern[redigera | redigera wikitext]
I stället för att arbeta med Hubblekonstanten är ett vanligt tillvägagångssätt att införa den dimensionslösa Hubbleparametern eller den reducerade Hubbleparametern vanligen betecknad med , och att skriva Hubbleparametern som (km/s)/Mpc,[27] således
All osäkerhet i värdet på överförs också till värdet på .[28]
Bestämma Hubblekonstanten[redigera | redigera wikitext]
Värdet för Hubblekonstanten beräknas genom att mäta rödförskjutningen hos avlägsna galaxer och sedan bestämma avstånd till samma galaxer (med någon annan metod än Hubbles lag). Osäkerheten i de fysiska förutsättningar som använts för att bestämma dessa avstånd har gett varierande värden på Hubblekonstanten.
Tidiga mätningar och diskussioner[redigera | redigera wikitext]
Under större delen av andra hälften av 1900-talet bestämdes värdet av till mellan 50 och 90 (km/s)/Mpc.
Värdet på Hubblekonstanten var ämnet för en lång och ganska bitter kontrovers mellan Gérard de Vaucouleurs, som hävdade värdet var ca 100, och Allan Sandage, som hävdade värdet var nära 50.[29] År 1996 hölls en debatt, där John Bahcall var moderator, mellan Gustav Tammann och Sidney van den Bergh på ett liknande sätt som den tidigare Shapley-Curtisdebatten om dessa två konkurrerande värden.
Aktuella mätningar[redigera | redigera wikitext]
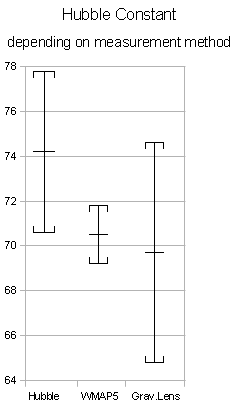
Den tidigare stora variationen i bestämningar blev delvis löst med införandet av Lambda-CDM-modellen för universumet i slutet av 1990-talet. Observationer av kluster med stora rödförskjutningar vid röntgen- och mikrovågsvåglängder med stöd av Siunjajev-Zeldovitj-effekten, mätningar av anisotropier i den kosmiska bakgrundsstrålningen och optiska undersökningar gav alla med Lambda-CDM-modellen ett värde på cirka 70 på konstanten.
Mätresultatens överensstämmelse mellan alla dessa metoder nedan stödjer både det uppmätta värdet på och Lambda-CDM modellen.
Med data från rymdteleskopet Hubble[redigera | redigera wikitext]
Hubble Space Telescope (HST) Key Project (lett av Wendy L. Freedman, Carnegie Observatories i Kalifornien) använde rymdteleskopet Hubble för att identifiera avstånd i universum och därmed av universums expansion med hjälp av en avstånd skala. Cepheid (pulserande stjärnor med ett samband mellan pulstid och ljusstyrka) och supernovor av typ IA (standardljus) tjänade som indikatorer för att beräkna Hubblekonstanten i maj 2001 till 72 ± 8 (km/s)/Mpc,[30] i överensstämmelse med en mätning av baserat på Siunjajev-Zeldovitj-effekten observationer av många rika galaxhopar som gav en liknande noggrannhet.
Med data från Spitzerteleskopet[redigera | redigera wikitext]
År 2012 kom Freedman med flera fram till Hubblekonstanten 74,3 ± 2,1 (km/s)/Mpc efter en omkalibrering av Cepheiders avståndsskala baserat på data från Spitzerteleskopet, Spitzer Space Telescope, baserat på observationer i våglängdsområdet 3–6 μm, medium infraröd,[31] kombinerat med WMAP7 och HST kosmologiska data. Eftersom Cepheidvariabler används för att fastställa galaktiska avstånd, i första hand för att kalibrera ljusstyrkan för närbelägna typ Ia supernovor, påverkade denna , vilken bestäms genom observationer av mer avlägsna typ Ia supernovor.
Med observationer av cepheider i Stora magellanska molnet från rymdteleskopet Hubble[redigera | redigera wikitext]
Riess et al. använde observationer av cepheider i det Stora magellanska molnet för en noggrannare kalibrering av cepheidernas avståndsskala och bestämde därigenom till 74,22 ± 1,82 (km/s)/Mpc[32].
Med observationer av rödjättegrenen i galaxer[redigera | redigera wikitext]
Freedman et al. observerade närbelägna galaxer i vilka man har observerat typ Ia supernovor och bestämde avstånden till dessa galaxer genom att bestämma ljusstyrkan för de ljusaste rödjättestjärnorna i dessa galaxer. På detta sätt kunde de kalibrera ljusstyrkan för typ Ia supernovorna och sedan använda mer avlägsna typ Ia supernovor för att bestämma Hubbles konstant till 69,8 ± 0,8 (stat) (sys) (km/s)/Mpc[33].
Med data från rymdteleskopet Chandra[redigera | redigera wikitext]
I augusti 2006 med hjälp av data från NASA:s Chandra-teleskop, Chandra X-ray Observatory, fann en grupp från NASAs George C. Marshall Space Flight Center (MSFC) Hubblekonstanten vara 77 (km/s)/Mpc med en osäkerhet på ca 15% genom att studera Siunjajev-Zeldovitj-effekten.[34]
Med data från rymdsonden WMAP[redigera | redigera wikitext]
Wilkinson Microwave Anisotropy Probe (WMAP) mäter temperaturfördelningen i elektromagnetisk strålning i mikrovågsområdet. Den kosmisk bakgrundsstrålningen ligger i mikovågsområdet. De mest exakta bestämningarna av kosmisk bakgrundsstrålning gav Hubblekonstanten 71 ± 4 (km/s)/Mpc med WMAP år 2003 och 70,4 +1.5−1.6 (km/s)/Mpc i mätningar fram till år 2006.[35] I rapporten omfattande fem år från WMAP 2008 gavs 71,9 +2,6−2,7 (km/s)/Mpc från endast WMAP-data och 70,1 ± 1,3 (km/s)/Mpc när data från andra studier införlivades,[36] medan rapporten för sju år släppt år 2010 gav 71,0 ± 2,5 (km/s)/Mpc från endast WMAP-data och 70,4 +1,3−1,4 (km/s)/Mpc när data från andra studier införlivades.[37]
Dessa värden fås genom att passa en kombination av WMAP-data och andra kosmologiska data till den enklaste versionen av Lambda-CDM modellen. Om data passas till mer allmänna versioner, tenderar att vara mindre och osäkrare: vanligtvis runt 67 ± 4 (km/s)/Mpc även om vissa modeller tillåter värden nära 63 (km/s)/Mpc.[38]
Den 20 dec 2012 är Hubblekonstanten, efter 9 års mätningar av WMAP, 70,0 ± 2,2 (km/s)/Mpc från endast WMAP-data och 69,32 ± 0,80 (km/s)/Mpc när data från andra studier införlivades.[39]
Med data från rymdsonden Planck[redigera | redigera wikitext]
Ytterligare observationer av mikrovågsbakgrunden har gjorts med högre precision från den europeiska rymdsonden Planck. I den slutliga analysen av dess resultat 2018 bestämdes Hubbles konstant till 67,4 ± 0,5 (km/s)/Mpc.[40]
Hubble-krisen[redigera | redigera wikitext]
Det har noterats av flera forskare under de senaste åren att värdet på Hubbles konstant från observationer av mikrovågsbakgrunden i det tidiga universum skiljer sig till synes signifikant från det värde som bestäms genom observationer av cepheider och typ Ia supernovor i det nutida universum. Allt noggrannare mätningar av mikrovågsbakgrunden ger ett värde på ca 67 (km/s)/Mpc medan observationer av cepheider och supernovor leder till värdet ca 73 (km/s)/Mpc. De båda metodernas statistiska felmarginal överlappar inte. Det är för närvarande inte klart huruvida detta indikerar en okänd fysikalisk effekt eller om det beror på systematiska fel i kalibreringen av observationerna[41][42].
Acceleration av expansionen[redigera | redigera wikitext]
Ett värde för decellerationskonstanten mätt med standardljuskälla observationer av supernovor av typen Ia, vilken fastställdes att vara negativ år 1998, förvånade många astronomer och med konsekvensen att universums expansion för närvarande "accelererar"[43] (även om Hubbleparametern fortfarande minskar med tiden, såsom anges i avsnittet Utläggning; se WP-artiklarna om mörk energi och Lambda-CDM modellen). Observationerna gjordes av två oberoende grupper ledda av Saul Perlmutter respektive av Brian Schmidt och Adam Riess.
Härledning av Hubbleparametern[redigera | redigera wikitext]
Börja med Friedmanns ekvation:
där är Hubbleparametern, är skalfaktorn, är gravitationskonstanten, är den normaliserade spatiala krökningen av universum och är −1, 0 eller +1 och är den kosmologiska konstanten.
Materia-dominerat universum (med en kosmologisk konstant)[redigera | redigera wikitext]
Om universum är materia-dominerat, då kan universums densitet bara inkludera materia så
där är massdensiteten i nutid. För icke-relativisiska partiklar vet vi att deras massdensitet minskar proportionellt mot inversen av universums volym så ekvationen ovan måste vara sann. Vi kan också definiera (se densitetsparametern )
så Också per definition,
och
där index 0 hänvisar till nuvarande värden och . Sätt in allt detta i Friedmanns ekvation i början av detta avsnitt och ersätt med så fås
Materia- och mörk energi-dominerat universum[redigera | redigera wikitext]
Om universum är både materia- och mörk energi-dominerat, då kommer ovanstående ekvation för Hubbleparametern också vara en funktion av tillståndsekvationen för mörk energi. Så nu:
där är energidensiteten för mörk energi. Per definition är en tillståndsekvation i kosmologi , och om vi sätta in detta i flödesekvationen som beskriver hur universums densitet utvecklas med tiden,
Om är konstant
Därför för mörk energi med en konstant tillståndsekvation , . Om vi sätter in detta i Friedmans ekvation på ett liknande sätt som tidigare, men denna gång sätter vilket förutsätter ett spatialt plant, inte krökt universum, (se universum)
Om mörk energi inte har ett konstant tillståndsekvation , då
och för att lösa detta måste vi parametrisera , till exempel om , fås
Enheter härledda från Hubblekonstanten[redigera | redigera wikitext]
Hubbletid[redigera | redigera wikitext]
Hubblekonstanten har enheten invers tid, dvs. s−1. Hubbletid (eng. Hubble time) definieras som . Värdet på Hubbletiden i den kosmologiska standardmodellen är 4,4×1017 s eller 13,8 miljarder år.[44]
Som nämnts ovan är det nuvarande värdet av Hubbleparametern . I en modell i vilken hastigheter är konstanta, minskar med tiden. I den naiva modellen där är konstant, skulle Hubbletiden vara tiden det tar för universum att öka i storlek med en faktor av e (eftersom lösningen av är där är storleken på någon funktion vid något godtyckligt initialt villkor ).
Över långa tidsperioder är dynamiken komplicerad på grund av allmänna relativitetsteorin, mörk energi, inflation, etc., såsom förklarats ovan.
Hubblelängd[redigera | redigera wikitext]
Hubblelängd (eng. Hubble length, Hubble distance) är en enhet för avstånd i kosmologi, definieras som - ljusets hastighet multiplicerat med Hubbletid. Den är ekvivalent med 4 228 miljoner parsec eller 13,8 miljarder ljusår. (Det numeriska värdet av Hubblelängd i ljusår är per definition lika med Hubbletid i år.) Hubblelängden skulle vara avståndet vid vilket galaxer just nu avlägsnar sig med ljusets hastighet, vilket kan ses genom att sätta in i ekvationen för Hubbles lag, .
Hubblevolym[redigera | redigera wikitext]
Hubblevolym (eng. Hubble volume) är ibland definierad som en volym av universum med en medflyttande (eng. comoving) storlek av . Den exakta definitionen varierar: Ibland definieras den, som volymen av ett sfär med radien eller alternativt en kub med sidan . Vissa kosmologer använder även termen Hubblevolym för att hänvisa till volymen av det observerbara universumet, även om denna har en radie ungefär tre gånger större.
En sfär med radien kallas en Hubblesfär och omsluter alltså en Hubblevolym. Det som är utanför Hubblesfären avlägsnar sig från dess centrum med en skenbar hastighet som överstiger ljusets, medan det som är inuti avlägsnar sig med hastigheter som understiger ljusets.
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Hubble's law, 22 januari 2013.
Noter[redigera | redigera wikitext]
- ^ Routledge Critical Dictionary of the New Cosmology. Routledge. 2001. sid. 202. ISBN 0-203-16457-1. http://books.google.com/?id=BgNGWVr5yhIC&pg=PA202
- ^ Lemaître, Georges (1927). ”Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques” (på franska) (pdf). Annales de la Société Scientifique de Bruxelles A47: sid. 49–56. http://adsabs.harvard.edu/cgi-bin/nph-data_query?bibcode=1927ASSB...47...49L&link_type=ARTICLE&db_key=AST&high=.. Översatt till engelska med strykningar: Lemaître, Georges (1931). ”Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulæ”. Monthly Notices of the Royal Astronomical Society 91: sid. 483–490.
- ^ van den Bergh, Sidney:The Curious Case of Lemaitre's Equation No. 24 , arxiv.org, 2011-06-06
- ^ Block, David L. ”Georges Lemaître and Stigler’s Law of Eponymy”. Arxiv.org. http://arxiv.org/abs/1106.3928.
- ^ Way, Michael and Nussbaumer, Harry: Lemaître’s Hubble relationship , Physics Today, Published online August 2011, doi:10.1063/PT.3.1194
- ^ Reich, Eugenie Samuel. ”Edwin Hubble in translation trouble”. Nature.com. http://www.nature.com/news/2011/110627/full/news.2011.385.html.
- ^ Livio, Mario: Mystery of the missing text solved, Nature, Vol 479, sid. 171–173, 10 november 2011
- ^ Hubble, Edwin:A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae Arkiverad 30 juni 2008 hämtat från the Wayback Machine. (1929) Proceedings of the National Academy of Sciences of the United States of America, Volume 15, March 15, 1929: Issue 3, sid. 168–173
- ^ Longair, Malcolm S (2006). The Cosmic Century. Cambridge University Press. ISBN 0-521-47436-1. http://books.google.com/?id=z0vlYHQZHJcC&pg=RA2-PA109
- ^ Wright, Edward L.: Homogeneity and Isotropy, Many Distances. Last modified 12 Jun 2009
- ^ Friedman, Alexander (1922). ”Über die Krümmung des Raumes”. Zeitschrift für Physik 10 (1): sid. 377–386. doi:. (Engelsk översättning: Friedman, A. (1999). ”On the Curvature of Space”. General Relativity and Gravitation 31 (12): sid. 1991–2000. doi:.)
- ^ "cepheid". NE.se. Läst 23 december 2014.
- ^ Sandage, Allan R. (maj,1958). ”Current Problems in the Extragalactic Distance Scale”. Astrophysical Journal 127 (3): sid. 513–526. doi:.
- ^ Kirshner, Robert P.:‘‘Hubble's Diagram and Cosmic Expansion’‘, PNAS, vol. 101, no. 1, 6 jan 2004
- ^ Isaacson, Walter (2007). Einstein: His Life and Universe. Simon and Schuster. sid. 354. ISBN 0-7432-6473-8. http://books.google.com/books?id=cdxWNE7NY6QC, Utdrag från sida 354
- ^ Science News: Einstein's Biggest Blunder? Dark Energy May Be Consistent With Cosmological Constant, Science Daily, 28 nov. 2007.
- ^ Davis, Tamara M. and Lineweaver, Charles H.: Superluminal Recessional Velocities’‘, AIP Conference Proceedings, vol. 555, sid. 348–351, doi: 10.1063/1.1363540, 2000, revised 2001
- ^ . Keel, William C. (2007). The Road to Galaxy Formation (2). Springer. sid. 7. ISBN 3-540-72534-2. http://books.google.com/?id=BUgJGypUYF0C&pg=PA7
- ^ Rothstein, Dave: ‘‘Is the universe expanding faster than the speed of light?’‘ Arkiverad 23 november 2003 hämtat från the Wayback Machine., set 2003, sista stycket.
- ^ Harrison, Edward (1992). ”The redshift-distance and velocity-distance laws”. Astrophysical Journal, Part 1 403: sid. 28–31. doi:.. A pdf file can be found here [1].
- ^ Madsen, Mark S. (1995). The Dynamic Cosmos: Exploring the Physical Evolution of the Universe. CRC Press. sid. 35. ISBN 0-412-62300-5. http://books.google.com/?id=_2GeJxVvyFMC&pg=PA35
- ^ Dekel, Avishai, and Ostriker, Jeremiah P (1999). Formation of Structure in the Universe. Cambridge University Press. sid. 164. ISBN 0-521-58632-1. http://books.google.com/?id=yAroX6tx-l0C&pg=PA164
- ^ Padmanabhan, Thanu (1993). Structure formation in the universe. Cambridge University Press. sid. 58. ISBN 0-521-42486-0. http://books.google.com/?id=AJlOVBRZJtIC&pg=PA58
- ^ Sartori, Leo (1996). Understanding Relativity. University of California Press. sid. 163, Appendix 5B. ISBN 0-520-20029-2
- ^ Sartori, Leo (1996). Understanding Relativity. University of California Press. sid. 304–305. ISBN 0-520-07986-8
- ^ Chase, Scott I.: Olbers' Paradox in the Physics FAQ; se också I. Asimov, ‘‘The Black of Night’‘, in Asimov on Astronomy (Doubleday, 1974), ISBN 0-385-04111-X.
- ^ Joakim Edsjö: Mörk materia och det tidiga universum Stockholms universitet, sid.10
- ^ Peebles, P.J.E., Principles of Physical Cosmology, Princeton University Press, 1993.
- ^ Overbye, Dennis Lonely Hearts of the Cosmos: The Scientific Quest for the Secret of the Universe Harper-Collins (1991), ISBN 0-06-015964-2 & ISBN 0-330-29585-3 (finalist, Nation Book Critics Circle Award for non-fiction). Second edition (with new afterword) Back Bay, 1999. Gives an account of the history of the dispute and rivalries.
- ^ W. L. Freedman, B. F. Madore, B. K. Gibson, L. Ferrarese, D. D. Kelson, S. Sakai, J. R. Mould, R. C. Kennicutt, Jr., H. C. Ford, J. A. Graham, J. P. Huchra, S. M. G. Hughes, G. D. Illingworth, L. M. Macri, P. B. Stetson (2001). ”Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant”. The Astrophysical Journal 553 (1): sid. 47–72. doi:. https://arxiv.org/abs/astro-ph/0012376..
- ^ Wendy L. Freedman; Madore, Barry F.; Scowcroft, Victoria; Burns, Chris; Monson, Andy; Persson, S. Eric; Siebert, Mark; Rigby, Jane (2012). ”Carnegie Hubble Program: A mid-infrared calibration of the Hubble constant”. Astrophysical Journal 758 (1): sid. 24. doi:.
- ^ Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., Scolnic, D. (2019). ”Large Magellanic Cloud cepheid standards provide a 1% foundation for the determination of the Hubble constant and stronger evidence for physics beyond $\Lambda$CDM”. Astrophysical Journal 876: sid. 85. https://iopscience.iop.org/article/10.3847/1538-4357/ab1422.
- ^ Freedman, W. L. et al. (2019). ”The Carnegie-Chicago Hubble program. VIII. An independent determination of the Hubble constant based on the tip of the red giant branch”. Astrophysical Journal 882: sid. 34. https://iopscience.iop.org/article/10.3847/1538-4357/ab2f73.
- ^ Chandra X-ray Center News Release: Chandra independently determines Hubble constant, Spaceflight Now, posted 8 aug. 2006
- ^ D. N. Spergel; Bean, R.; Dore, O.; Nolta, M. R.; Bennett, C. L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; et al. (2007). ”Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology”. Astrophysical Journal Supplement Series 170 (2): sid. 377–408. doi:. https://arxiv.org/abs/astro-ph/0603449.; available online at LAMBDA
- ^ Tabell 7, sidan 54, i Hinshaw (2009). ”Five-Year Wilkinson Microwave Anisotropy Probe Observations: Data Processing, Sky Maps, and Basic Results”. The Astrophysical Journal Supplement 180 (2): sid. 225–245. doi:. https://arxiv.org/abs/0803.0732.
- ^ ”Seven-Year Wilson Microwave Anisotropy Probe (WMAP) Observations: Sky Maps, Systematic Errors, and Basic Results” (PDF). nasa.gov. http://lambda.gsfc.nasa.gov/product/map/dr4/pub_papers/sevenyear/basic_results/wmap_7yr_basic_results.pdf. Läst 2 december 2010. (see p. 39 for a table of best estimates for various cosmological parameters)
- ^ Results for H0 and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website Arkiverad 9 juli 2014 hämtat från the Wayback Machine..
- ^ Bennet, C L et al: Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations:Final Maps and Results , 2012
- ^ Planck Collaboration (2020). ”Planck 2018 results. VI. Cosmological parameters”. Astronomy & Astrophysics (EDP Sciences) 641: sid. A6. https://www.aanda.org/articles/aa/full_html/2020/09/aa33910-18/aa33910-18.html.
- ^ Panek, R. (2020). ”A cosmic cricis”. Scientific American (Mars).
- ^ Crane, Leah (2022). ”Clashing figures for universe's growth are starting to look more serious”. New Scientist Vol 253 (No 3371): sid. 10.
- ^ S. Perlmutter, Supernovae, Dark Energy, and the Accelerating Universe, Physics Today, April 2003, pp 53–60 [2] Arkiverad 4 mars 2016 hämtat från the Wayback Machine.
- ^ Liddle, Andrew R. (2003). An Introduction to Modern Cosmology (2nd). Chichester: Wiley. ISBN 0-470-84835-9



















































































