Allmänna relativitetsteorin

Allmänna relativitetsteorin är den geometriska teori om gravitationen som Albert Einstein publicerade 1915[1] och den aktuella beskrivningen av gravitationen inom den moderna fysiken. Allmänna relativitetsteorin generaliserar den speciella relativitetsteorin och Newtons gravitationslag, och ger därmed en enhetlig beskrivning av gravitation som en geometrisk egenskap hos rum och tid, eller rumtid. I synnerhet är krökningen av rumtiden direkt relaterad till energin och rörelsemängden hos den materia och strålning som är närvarande. Förhållandet specificeras av Einsteins fältekvationer, ett system av partiella differentialekvationer.
Några av den allmänna relativitetsteorins förutsägelser skiljer sig markant från den klassiska fysikens, särskilt de om tidens förlopp, rymdens geometri, rörelsen hos kroppar i fritt fall och ljusets spridning. Exempel på sådana skillnader är gravitationell tidsdilatation, gravitationslinser, gravitationell rödförskjutning av ljus och gravitationell tidsfördröjning. Den allmänna relativitetsteorins förutsägelser har bekräftats av alla hittills gjorda observationer och experiment. Även om den allmänna relativitetsteorin inte är den enda relativistiska gravitationsteorin, är det den enklaste teorin som samtidigt är förenlig med experimentella data. Obesvarade frågor återstår emellertid – den mest grundläggande är hur allmänna relativitetsteorin ska kunna förenas med kvantmekanikens lagar för att bilda en komplett teori utan självmotsägelser om kvantgravitation.
Einsteins teori har viktiga astrofysikaliska konsekvenser. Exempelvis implicerar den existensen av svarta hål – regioner i rymden i vilka rum och tid förvrängs på ett sådant sätt att ingenting, inte ens ljuset, kan undkomma – som ett slutligt tillstånd för massiva stjärnor. Det finns gott om bevis för att den intensiva strålning som avges av vissa typer av astronomiska objekt beror på svarta hål. Exempelvis uppkommer mikrokvasarer och aktiva galaxkärnor till följd av att det finns stellära svarta hål respektive supermassiva svarta hål. Ljusets böjning av gravitationen kan leda till fenomenet gravitationslinser, där flera bilder av samma avlägsna astronomiska objekt är synliga på himlen. Allmänna relativitetsteorin förutsäger också existensen av gravitationsvågor, vilka också har observerats direkt av LIGO. Dessutom utgör den allmänna relativitetsteorin grunden för aktuella kosmologiska modeller av ett expanderande universum.
Historia[redigera | redigera wikitext]

Strax efter publiceringen av den speciella relativitetsteorin (1905) började Einstein tänka på möjligheten att införliva gravitationen i sitt nya relativistiska ramverk. År 1907, med början i ett enkelt tankeexperiment med en observatör i fritt fall, inledde han ett åttaårigt sökande efter en relativistisk gravitationsteori. Efter många omvägar och misslyckade försök kulminerade hans arbete i presentationen vid den preussiska vetenskapsakademien i november 1915 av vad som idag kallas Einsteins fältekvationer. Dessa ekvationer anger hur rymdens geometri och tiden påverkas av närvaron av materia och energi och utgör kärnan i Einsteins allmänna relativitetsteori.[2]
Einsteins fältekvationer är icke-linjära och mycket svåra att lösa. Einstein använde approximationsmetoder vid utarbetandet av de första förutsägelserna av teorin. Så tidigt som 1916 hittade astrofysikern Karl Schwarzschild den första icke-triviala exakta lösningen till Einsteins fältekvationer, Schwarzschildmetriken. Denna lösning lade grunden för beskrivningen av slutskedet av en gravitationskollaps och de objekt som idag är kända som svarta hål. Samma år togs de första stegen mot att generalisera Schwarzschilds lösning till elektriskt laddade objekt, som så småningom resulterade i Reissner–Nordströms lösning, nu i samband med elektriskt laddade svarta hål.[3] År 1917 tillämpade Einstein sin teori på universum som helhet och inledde forskningsområdet relativistisk kosmologi. I linje med samtida tänkande antog han ett statiskt universum och lade därför till en ny parameter till de ursprungliga fältekvationerna – den kosmologiska konstanten – vilken gjorde ekvationerna förenliga med detta antagande om en statisk värld.[4] År 1929 hade dock Hubble och andra visat att universum expanderar, vilket kan beskrivas med de expanderande kosmologiska lösningar som hittades av Friedmann (1922) och som inte kräver en kosmologisk konstant. Lemaître använde dessa lösningar för att formulera den tidigaste versionen av Big Bang-modellen, i vilken vårt universum har utvecklats från ett mycket varmt initialt tillstånd med hög densitet.[5] Einstein förklarade senare att införandet av den kosmologiska konstanten var hans livs största misstag.[6] Ett uttalande som skulle visa sig vara förhastat, se avsnittet Kosmologi nedan.
Under de första decennierna förblev den allmänna relativitetsteorin något av en kuriositet bland fysikaliska teorier. Den var helt klart överlägsen newtonsk gravitation, samt förenlig med speciella relativitetsteorin och förklarade flera fenomen som inte kunde förklaras av den newtonska teorin. Einstein själv visade 1915 hur hans teori förklarade planeten Merkurius avvikande periheliumprecession utan godtyckliga parametrar (”fiffelfaktorer”).[7] På liknande sätt bekräftade en forskningsresa, ledd av Arthur Eddington, under den totala solförmörkelsen 29 maj 1919 den allmänna relativitetsteorins förutsägelse att solen böjer av stjärnljus,[8] vilket omedelbart gjorde Einstein världskänd.[9] Men teorin kom in i huvudfåran av teoretisk fysik och astrofysik först i och med utvecklingen mellan cirka 1960 och 1975, en period numera känd som den gyllene åldern för den allmänna relativitetsteorin.[10] Fysiker började förstå svarta hål och identifierade kvasarer som ett slag av sådana objekt.[11] Allt mer exakta tester av solsystemet bekräftade teorins förmåga till förutsägelser[12] och relativistisk kosmologi blev föremål för direkta observationella tester.[13]
Från klassisk mekanik till allmänna relativitetsteorin[redigera | redigera wikitext]
Den allmänna relativitetsteorin kan förstås genom att undersöka dess likheter med och avvikelser från klassisk fysik. Det första steget är insikten att klassisk mekanik och Newtons gravitationslag medger en geometrisk beskrivning. Kombinationen av denna beskrivning med lagarna i den speciella relativitetsteorin resulterar i en heuristisk härledning av den allmänna relativitetsteorin.[14]
Geometri för newtonsk gravitation[redigera | redigera wikitext]

Den klassiska mekanikens grund är att en kropps rörelse kan beskrivas som en kombination av fri (eller trög) rörelse och avvikelser från denna fria rörelse. Dessa avvikelser orsakas av yttre krafter som verkar på en kropp i enlighet med Newtons andra rörelselag, enligt vilken nettokraften som verkar på en kropp är lika med kroppens tröga massa multiplicerad med dess acceleration.[15] De uppkomna tröghetsrörelserna är relaterade till tidens och rummets geometri: i standardreferensramar inom klassisk mekanik rör sig objekt i fritt fall längs räta linjer med konstant hastighet. Med modernt språkbruk är deras vägar geodeter, räta världslinjer i en krökt rumtid.[16]
Omvänt kan man förvänta sig att tröghetsrörelser – identifierade genom att observera verkliga rörelser hos kroppar och med justeringar för yttre krafter (såsom elektromagnetism och friktion) – kan användas för att definiera rymdgeometrin såväl som en tidskoordinat. Det blir dock tvetydigt när gravitationen kommer in i bilden. Enligt Newtons gravitationslag – oberoende verifierad av experiment som det av Loránd Eötvös och hans efterföljare (se Eötvösexperimentet) – finns det en universell ekvivalens mellan trög och tung massa (även känd som den svaga ekvivalensprincipen). Banan för en testkropp i fritt fall beror enbart på dess position och utgångshastighet, men inte på någon av dess materiella egenskaper.[17] En förenklad version av detta införlivas i Einsteins hissexperiment som illustreras i figuren till höger: en observatör i ett litet slutet rum kan inte, genom att observera en fallande kropps bana, avgöra huruvida rummet är i vila i ett gravitationsfält eller ombord på en raket som accelererar i en takt som motsvarar gravitationsfältets tyngdacceleration.[18]
Enligt ekvivalensprincipen finns det ingen observerbar skillnad mellan tröghetsrörelse och rörelse under inverkan av gravitationskraften. Detta leder till definitionen av en ny klass av tröghetsrörelse, nämligen den för objekt i fritt fall under inverkan av gravitation. Denna nya klass av föredragna rörelser definierar också rumtidens geometri – i matematiska termer är det en geodetisk rörelse associerad med en specifik förbindelse som beror på gradienten av gravitationspotentialen. Rummet, i denna konstruktion, har fortfarande vanlig euklidisk geometri. Rumtiden i sin helhet är dock mer komplicerad, vilket kan påvisas med enkla tankeexperiment som att följa banor för olika fritt fallande testpartiklar: resultatet av transporter av rumtidsvektorer som beskriver en partikels hastighet (tidsliknande vektor) kommer att variera med partikelns bana. Matematiskt sett är den newtonska förbindelsen inte integrerbar. Av detta kan man dra slutsatsen att rumtiden är krökt. Den resulterande teorin är en geometrisk formulering av newtonsk gravitation som enbart använder kovarianta begrepp, det vill säga en beskrivning som gäller i alla koordinatsystem.[19] I denna geometriska beskrivning är tidvattenkrafter – den relativa accelerationen hos kroppar i fritt fall – relaterade till förbindelsens derivata, som visar hur närvaron av massa orsakar en modifierad geometri.[20]
Relativistisk generalisering[redigera | redigera wikitext]

Hur fascinerande geometrisk newtonsk gravitation än kan vara är dess grund – klassisk mekanik – enbart ett gränsfall av (speciell) relativistisk mekanik.[21] I termer av symmetrier: där gravitation kan försummas är fysiken Lorentzinvariant liksom i den speciella relativitetsteorin snarare än Galileiinvariant som inom klassisk mekanik. (Den definierande symmetrin hos speciella relativitetsteorin är Poincarégruppen, vilken inkluderar translationer och rotationer.) Skillnaderna mellan de två blir betydande när det gäller hastigheter som närmar sig ljusets och för högenergifenomen.[22]
Med Lorentzsymmetri uppträder ytterligare strukturer som definieras av ljuskoner (se bild). Ljuskonerna definierar en kausal struktur: för varje händelse A finns det en mängd händelser som i princip antingen kan påverka eller påverkas av A via signaler eller interaktioner som inte behöver färdas snabbare än ljuset (såsom händelse B i bilden) och en mängd händelser för vilka en sådan påverkan är omöjlig (såsom händelse C i bilden). Denna uppdelning av rumtiden är observatörsoberoende.[23] Tillsammans med världslinjerna för fritt fallande partiklar kan ljuskoner användas för att rekonstruera rumtidens semi-Riemannska metrik, minst upp till en positiv skalär faktor. I matematiska termer definieras en konform struktur,[24] eller mer precist en konform geometri.
Speciella relativitetsteorin definieras i frånvaro av gravitation. För praktiska tillämpningar är det en lämplig modell när gravitationen kan försummas. Genom att föra in gravitationen, och förutsätta ekvivalensprincipen, gäller ett analogt resonemang liksom i föregående avsnitt: det finns inga globala tröghetssystem. Istället finns det approximativa tröghetssystem som rör sig tillsammans med fritt fallande partiklar. I rumtiden deformeras de räta tidsliknande linjer som definierar ett gravitationsfritt tröghetssystem, till linjer som är krökta relativt varandra, vilket antyder att inklusionen av gravitationen kräver en förändring i rumtidsgeometrin.[25]
A priori är det inte klart huruvida de nya fritt fallande lokala systemen är referenssystem i vilka den speciella relativitetsteorins lagar gäller – denna teori är baserad på ljusets spridning och därmed även på elektromagnetismen, som skulle kunna ha en annan uppsättning preferensramar. Med hjälp av olika antaganden om de speciella relativistiska ramarna (såsom att de är jordfixerade, eller i fritt fall) kan man dock härleda olika förutsägelser för den gravitationella rödförskjutningen, det vill säga hur ljusfrekvensen skiftar beroende på hur ljusets färdas genom ett gravitationsfält (se nedan). Faktiska mätningar visar att de fritt fallande systemen är de i vilka ljuset utbreder sig såsom det gör enligt den speciella relativitetsteorin.[26] Generaliseringen av denna redogörelse – nämligen att lagarna i speciella relativitetsteorin gäller med god approximation i lokala fritt fallande (icke-roterande) referenssystem – är känd som Einsteins ekvivalensprincip, en viktig ledstjärna för att generalisera speciell relativistisk fysik till att inkludera gravitation.[27]
Samma experimentella data visar att tiden mätt med klockor i ett gravitationsfält – egentiden (proper time) – inte följer speciella relativitetsteorins regler. I rumtidsgeometriska termer är den inte mätt av metriken i Minkowskirummet. Liksom i det newtonska fallet antyder detta en mer allmän geometri. För små skalor är alla referensramar i fritt fall ekvivalenta och approximativt minkowskiska. Av detta följer att vi nu har att göra med en krökt generalisering av Minkowskirum. Den metriska tensor som definierar geometrin – i synnerhet hur längd och vinklar mäts – är inte Minkowskimetriken i speciella relativitetsteorin, utan en generalisering känd som semi- eller pseudo-Riemannsk metrik. Vidare är varje Riemannsk metrik naturligt associerad med en viss typ av förbindelse, Levi-Civita-förbindelsen, och det är i själva verket denna förbindelse som uppfyller ekvivalensprincipen och ger upphov till ett lokalt minkowski-rum (det vill säga, att i lämpliga lokala tröghetskoordinater, är metriken minkowskisk och dess första partiella derivator och förbindelsekoefficienterna försvinner).[28]
Einsteins ekvationer[redigera | redigera wikitext]
Efter att ha formulerat den relativistiska, geometriska versionen av gravitationens effekter, kvarstår frågan om gravitationens källa. I newtonsk gravitation är källan massa. I speciella relativitetsteorin framställs massan som en mer generell kvantitet som kallas energi–rörelsemängd-tensor, vilken inkluderar både energi- och rörelsemängdstätheter såväl som spänning (det vill säga tryck och skjuvning).[29] Genom att använda ekvivalensprincipen generaliseras tensorn lätt till krökt rumtid. Genom att utvidga analogin med geometrisk newtonsk gravitation, är det naturligt att anta att fältekvationen för gravitation avser denna tensor och Riccitensorn, vilken beskriver en viss klass av tidvatteneffekter: volymförändringen i ett litet moln med testpartiklar som initialt är i vila, och sedan faller fritt. Bevarande av energi och rörelsemängd motsvaras i den speciella relativitetsteorin av påståendet att energi-rörelsemängdstensorn är divergensfri. Denna formel är också lätt att generalisera till krökt rumtid genom att ersätta partiella derivator med sina motsvarigheter i krökta mångfalder, kovarianta derivator inom differentialgeometri. Med detta extra villkor – att den kovarianta divergensen av energi–rörelsemängd-tensorn, och följaktligen högerledet av ekvationen, är noll – får man den enklaste uppsättningen ekvationer, de som är kända som Einsteins (fält)ekvationer:
Einsteintensorn i vänsterledet är en divergensfri kombination av Riccitensorn och metriken. är symmetrisk.
är krökningsskalären. Riccitensorn själv är relaterad till Riemanns krökningstensor – som är mer generell – enligt
i högerledet är energi–rörelsemängd-tensorn. Alla tensorer är skrivna i abstrakt indexnotation.[30] Einsteintensorn är den enda divergensfria tensorn som är en funktion av de metriska koefficienterna, deras första och andra derivata, och som tillåter rumtiden i speciella relativitetsteorin som en lösning i frånvaro av gravitationskällor.[31] Tensorerna i båda leden är av andra graden, det vill säga att de kan ses som 4 × 4-matriser som var och en innehåller tio termer; därmed representerar ovanstående tio kopplade ekvationer. Som en följd av geometriska relationer kända som Bianchiidentiteter, uppfyller Einsteintensorn ytterligare fyra identiteter vilket reducerar antalet oberoende ekvationer till sex.[32]
Genom att matcha teorins förutsägelser med observerade planetbanor (eller, ekvivalent, att säkerställa att resultatet för svag gravitation och låg hastighet är newtonsk mekanik) kan proportionalitetskonstanten fixeras till κ = 8πG/c4, där G är gravitationskonstanten och c är ljusets hastighet.[33] När det inte finns någon materia närvarande, så att energi–rörelsemängd-tensorn försvinner, är resultatet Einsteins ekvationer för vakuum,
Alternativ till allmänna relativitetsteorin[redigera | redigera wikitext]
Det finns alternativ till allmänna relativitetsteorin som bygger på samma premisser, vilka inkluderar ytterligare regler och/eller restriktioner, vilket leder till andra fältekvationer – exempelvis Brans–Dickes teori, teleparallelism och Einstein–Cartans teori.[34]
Definition och grundläggande tillämpningar[redigera | redigera wikitext]
Härledningen som beskrivs i föregående avsnitt innehåller all information som behövs för att definiera den allmänna relativitetsteorin, beskriva dess viktigaste egenskaper och ta itu med en fråga av avgörande betydelse inom fysiken, nämligen hur teorin kan användas för modellbyggande.
Definition och grundläggande egenskaper[redigera | redigera wikitext]
Allmänna relativitetsteorin är en metrisk teori om gravitation. Dess kärna är Einsteins fältekvationer, vilka beskriver relationen mellan en fyrdimensionell pseudo-Riemannsk mångfald som representerar rumtidens geometri och energi–rörelsemängdstensorn som finns i rumtiden.[35] Fenomen som inom klassisk mekanik tillskrivs gravitationsverkan (såsom fritt fall, banrörelser, och rymdfarkosters flygbanor), motsvarar tröghetsrörelse i en krökt rumtidsgeometri i allmänna relativitetsteorin; det finns inga gravitationsavböjande objekt från deras naturliga, räta banor. Istället motsvarar gravitationen förändringar i rummets och tidens egenskaper, vilket i sin tur ändrar de mest räta banor som är möjliga som objekt naturligt kommer att följa.[36] Krökningen i sin tur orsakas av materians energi och rörelsemängd. Som John Wheeler har uttryckt det: rumtiden talar om för materian hur den skall förflytta sig, materian talar om för rumtiden hur den skall kröka sig.[37]
Medan den allmänna relativitetsteorin ersätter den skalära gravitationspotentialen inom klassisk fysik med en symmetrisk tensor av andra ordningen, reduceras den senare till den förra i vissa begränsade fall. För svaga gravitationsfält och låg hastighet relativt till ljusets hastighet, konvergerar teorins förutsägelser mot Newtons gravitationslags.[38]
Eftersom den är konstruerad med hjälp av tensorer, uppvisar allmänna relativitetsteorin generell kovarians: dess lagar – och andra lagar formulerade inom den allmänna relativitetsteorins ram – har samma form i alla koordinatsystem.[39] Dessutom innehåller teorin inte några invarianta geometriska bakgrundsstrukturer, alltså är den bakgrundsoberoende. Den uppfyller således en mer sträng allmän relativitetsprincip, nämligen att fysikens lagar är desamma för alla observatörer.[40] Lokalt, såsom den är uttryckt i ekvivalensprincipen, är rumtiden Minkowskisk, och fysikens lagar uppvisar lokal Lorentzinvarians.[41]
Modellbyggande[redigera | redigera wikitext]
Kärnkonceptet för allmänt relativistiskt modellbyggande är en lösning av Einsteins fältekvationer. Givet både Einsteins ekvationer och lämpliga ekvationer för materiens egenskaper, består en sådan lösning av en pseudo-Riemannsk mångfald (vanligtvis definierad av metriken i specifika koordinater), och specifika materiefält definierade på denna mångfald. Materia och geometri måste uppfylla Einsteins ekvationer. I synnerhet måste materians energi–rörelsemängd-tensor vara divergensfri. Materian måste naturligtvis även uppfylla extra ekvationer som är påtvingade på grund av dess egenskaper. Kort sagt, en sådan lösning är ett modelluniversum som uppfyller allmänna relativitetsteorins lagar, och eventuella ytterligare lagar som gäller för materian.[42]
Einsteins ekvationer är icke-linjära partiella differentialekvationer och, som sådana, svåra att lösa exakt.[43] Likväl är ett antal exakta lösningar kända, men enbart ett fåtal av dem har direkta fysikaliska tillämpningar.[44] De mest kända exakta lösningarna, även de mest intressanta ur fysikalisk synvinkel, är Schwarzschildlösningen, Reissner–Nordström-lösningen och Kerrmetriken, som var och en motsvarar en typ av svart hål i ett annars tomt universum,[45] samt Friedmann–Lemaître–Robertson–Walker- och de Sitter-universum, som båda beskriver ett expanderande kosmos.[46] Exakta lösningar av stort teoretiskt intresse är Gödeluniversum (som öppnar upp fascinerande möjligheter för tidsresor i krökt rumtid), Taub–NUT-lösningen (en modell av universum som är homogen, men anisotrop) och anti-de Sitter-rum (som nyligen har blivit viktigt i samband med vad som kallas för Maldacenas förmodan).[47]
På grund av svårigheten att hitta exakta lösningar till Einsteins fältekvationer löses de ofta genom numerisk integrering på en dator eller genom att överväga små perturbationer av exakta lösningar. Inom numerisk relativitetsteori används kraftfulla datorer för att simulera rumtidsgeometrin och lösa Einsteins ekvationer för intressanta situationer såsom två kolliderande svarta hål.[48] I princip kan sådana metoder tillämpas på alla system, givet tillräckligt med datorresurser, och fundamentala frågor som nakna singulariteter kan tas itu med. Ungefärliga lösningar kan också hittas genom störningsteoretiska metoder som linjäriserad gravitation[49] och dess generalisering, postnewtonsk expansion, båda utvecklade av Einstein. Den senare beskriver en systematisk strategi för att lösa rumtidsgeometrin som innehåller en fördelning av materia som rör sig sakta jämfört med ljusets hastighet. Expansionen involverar en serie termer; den första termen representerar newtonsk gravitation, medan de senare termerna representerar mindre korrigeringar av Newtons teori på grund av allmänna relativitetsteorin.[50] En utvidgning av denna expansion är parametriserad postnewtonsk formalism (PPN), som möjliggör kvantitativa jämförelser mellan allmänna relativitetsteorins förutsägelser och alternativa teorier.[51]
Konsekvenser av Einsteins teori[redigera | redigera wikitext]
Allmänna relativitetsteorin har ett antal fysikaliska konsekvenser. Vissa följer direkt från teorins axiom, medan andra upptäckts först under de många år av forskning som följde Einsteins första offentliggörande.
Gravitationell tidsdilatation och frekvensskift[redigera | redigera wikitext]

Förutsatt att ekvivalensprincipen gäller,[52] påverkar gravitationen tidsförloppet. Ljus som skickas ned i en gravitationsbrunn förskjuts mot högre frekvenser (blåförskjutning) och ljus som skickas i den motsatta riktningen förskjuts mot lägre frekvenser (rödförskjutning). Dessa effekter kallas för gravitationellt frekvensskift. Mer allmänt förlöper processer nära en massiv kropp långsammare jämfört med processer som äger rum längre bort; denna effekt kallas för gravitationell tidsdilatation.[53]
Rödförskjutning orsakad av gravitation har mätts i laboratoriet[54] och med hjälp av astronomiska observationer.[55] Gravitationell tidsdilatation i jordens gravitationsfält har mätts flera gånger med atomur,[56] till exempel genom Hafele-Keating experimentet. Pågående validering tillhandahålls som en bieffekt av driften av Global Positioning System (GPS).[57] Tester i starkare gravitationsfält sker genom observationer av binära pulsarer.[58] Alla resultat överensstämmer med den allmänna relativitetsteorin,[59] men på den nuvarande nivån av noggrannhet, kan dessa observationer inte skilja mellan allmän relativitetsteori och andra teorier i vilka ekvivalensprincipen gäller.[60]
Ljusets böjning och gravitationell tidsfördröjning[redigera | redigera wikitext]

Allmänna relativitetsteorin förutsäger att ljusets bana böjs i ett gravitationsfält; ljus som passerar en massiv kropp böjs i riktning mot kroppen. Denna effekt har bekräftats genom att observera att ljuset från stjärnor eller avlägsna kvasarer böjs när det passerar nära solen.[61]
Dessa och relaterade förutsägelser följer av det faktum att ljuset följer vad som kallas nollgeodetiska banor – en generalisering av de räta linjer längs vilka ljuset färdas enligt klassisk fysik. Sådana geodeter är en generalisering av ljushastighetens invarians i den speciella relativitetsteorin.[62] Då lämpliga modellrumtider prövas (antingen yttre Schwarzschildlösningen eller, för mer än en enda massa, postnewtonsk expansion),[63] uppstår flera gravitationseffekter på ljusspridning. Även om ljusets böjning också kan härledas genom att utvidga universaliteten av fritt fall till ljus,[64] har avböjningsvinkeln till följd av sådana beräkningar enbart det halva värdet som ges av allmänna relativitetsteorin.[65]
Nära besläktat med ljusböjning är gravitationell tidsfördröjning (eller Shapirofördröjning), nämligen fenomenet att ljussignaler tar längre tid att gå genom ett gravitationsfält än de skulle i frånvaro av detta fält. Det har förekommit många framgångsrika tester av denna förutsägelse.[66] I parametriserad postnewtonsk formalism (PPN) bestämmer mätningar av både ljusböjning och gravitationell tidsfördröjning en parameter γ, som representerar inverkan av gravitationskraften på rymdgeometrin.[67]
Gravitationsvågor[redigera | redigera wikitext]

Enligt Albert Einsteins förutsägelse (1916)[68][69] finns det gravitationsvågor, det vill säga krusningar i rumtidens metrik som sprider sig med ljusets hastighet. Det är en av flera analogier mellan svaga gravitationsfält och elektromagnetism eftersom de är analoga med elektromagnetiska vågor. Den enklaste typen av sådan våg kan visualiseras genom sin verkan på en ring av fritt svävande partiklar. En gravitationsvåg som färdas genom ringen i riktning mot läsaren förvränger ringen på ett karaktäristiskt, rytmiskt sätt (se animerad bild till höger).[70] Sådana vågor observerades första gången indirekt genom förlusten av energi i det binära pulsarsystemet PSR B1913+16 (Hulse–Taylor-binären), vilket belönades med Nobelpriset i fysik 1993.[71]
Den 11 februari 2016 meddelade Advanced LIGO-teamet att de direkt hade detekterat gravitationsvågor från två svarta hål som slogs samman.[72][73][74] Förutom LIGO planeras eller pågår andra projekt för att försöka att observera effekterna av gravitationsvågor, till exempel ESA:s Laser Interferometer Space Antenna och försök att kombinera observationer av millisekundspulsarer för att detektera gravitationsvågor med ultralåg frekvens (~ 10-9 till 10-8 Hz).[75]
Då Einsteins ekvationer är icke-linjära, kommer godtyckligt starka gravitationsvågor inte att uppfylla kraven för superpositionsprincipen, vilket gör deras beskrivning besvärlig. För svaga fält, kan en linjär approximation emellertid göras. Sådana linjäriserade gravitationsvågor är tillräckligt noggranna för att beskriva de ytterst svaga vågor som förväntas anlända här på jorden från fjärran kosmiska händelser, vilka normalt resulterar i att relativa avstånd ökar och minskar med 10−21 eller mindre. Dataanalysmetoder gör rutinmässigt bruk av det faktum att dessa linjäriserade vågor kan vara Fourieruppdelade.[76]
Några exakta lösningar beskriver gravitationsvågor utan approximation, exempelvis ett vågpaket som färdas genom tomrum[77] eller Gowdyuniversum, varianter av ett expanderande kosmos fyllt med gravitationsvågor.[78] För gravitationsvågor som produceras i astrofysikaliskt relevanta situationer, exempelvis sammanslagningen av två svarta hål, är dock numeriska metoder för närvarande det enda sättet att konstruera lämpliga modeller.[79]
Orbitala effekter och riktningens relativitet[redigera | redigera wikitext]
Allmänna relativitetsteorin skiljer sig från den klassiska mekaniken i ett antal förutsägelser om kretsande kroppar. Den förutspår en total rotation (precession) av planetbanor samt förändringar av banor som orsakas av gravitationsvågor och effekter relaterade till riktningens relativitet.
Precession av apsis[redigera | redigera wikitext]

I allmänna relativitetsteorin, kommer apsis (den punkt i den kretsande kroppens bana som är närmast systemets masscentrum) att precessera – banan är inte en ellips, men liknar en ellips vars storaxel roterar, vilket resulterar i en rosliknande form (se bild). Einstein härledde först detta resultat genom att använda en ungefärlig metrik som representerar den newtonska gränsen och behandlade den kretsande kroppen som en testpartikel. Hans teori gav en enkel förklaring till den avvikande precessionen hos planeten Merkurius perihelium, vilken upptäckts av Urbain Le Verrier 1859. Detta var för Einstein ett viktigt bevis för att han äntligen hade identifierat de korrekta ekvationerna för gravitationsfältet.[80]
Effekten kan också härledas genom att använda den exakta Schwarzschildmetriken (som beskriver rumtiden kring en sfärisk massa)[81] eller den mer generella postnewtonska formalismen.[82] Precessionen beror på gravitationens påverkan på rymdens geometri och bidrag till en kropps egenenergi (olinjärt kodade i Einsteins ekvationer).[83] Relativistisk precession har observerats för alla planeter (Merkurius, Venus och jorden) för vilka noggranna mätningar av precessionen är möjliga.[84] och även för binära pulsarer för vilka precessionen är fem tiopotenser större.[85]
Orbitala störningar[redigera | redigera wikitext]

Enligt allmänna relativitetsteorin utsänder ett binärt system gravitationsvågor och förlorar därmed energi. På grund av denna förlust, minskar avståndet mellan de två kretsande kropparna och därmed deras omloppstid. Inom solsystemet eller för dubbelstjärnor, är effekten för liten för att kunna observeras. Detta är inte fallet för en binär pulsar med litet avstånd mellan komponenterna, ett system med två kretsande neutronstjärnor, varav en är en pulsar. Från pulsaren får observatörer på jorden en regelbunden serie av radiopulser som kan fungera som en mycket exakt klocka och som möjliggör noggranna mätningar av omloppsperioden. Eftersom neutronstjärnor är mycket kompakta, är det stora mängder energi som avges i form av gravitationsstrålning.[87]
Den första observationen av en minskning av omloppstiden på grund av gravitationsvågor gjordes av Hulse och Taylor, med hjälp av den binära pulsaren PSR B1913+16 som de upptäckte 1974. Detta var den första upptäckten av gravitationsvågor, om än indirekt, för vilken de tilldelades 1993 års nobelpris i fysik.[88] Sedan dess har flera andra binära pulsarer upptäckts, i synnerhet dubbelpulsaren PSR J0737-3039, där båda objekten är pulsarer.[89]
Geodetisk precession och ramdragning[redigera | redigera wikitext]
Flera relativistiska effekter är direkt relaterade till riktningens relativitet.[90] En av dessa är geodetisk precession: axelriktningen av ett gyroskop i fritt fall i krökt rumtid kommer att förändras i jämförelse med exempelvis riktningen för ljuset som mottas från avlägsna stjärnor – även om ett sådant gyroskop representerar möjligheten att hålla en riktning så stabil som möjligt (”parallelltransport”).[91] För månen–jorden-systemet har denna effekt mätts med hjälp av Lunar Laser Ranging (LLR).[92] På senare tid har den mätts för testmassor ombord på satelliten Gravity Probe B med en precision som är bättre än 0,3 %.[93][94]
Nära en roterande massa förekommer det gravitomagnetiska effekter, eller ramdragningseffekter. En avlägsen observatör kommer bestämma att objekt nära massan ”dras runt”. Denna effekt är mest extrem för roterande svarta hål, för varje objekt som träder in i en zon känd som ergosfären, är rotation oundviklig.[95] Sådana effekter kan återigen testas genom deras inflytande på orienteringen av gyroskop i fritt fall.[96] Något kontroversiella tester har utförts med hjälp av LAGEOS-satelliterna, vilka bekräftar den relativistiska förutsägelsen.[97] Även rymdsonden Mars Global Surveyor som kretsar kring Mars har använts.[98][99]
Astrofysikaliska tillämpningar[redigera | redigera wikitext]
Gravitationslinser[redigera | redigera wikitext]

Ljusets böjning genom gravitation ger upphov till en ny klass av astronomiska fenomen. Om ett massivt objekt ligger mellan en astronom och ett avlägset objekt med lämplig massa och relativa avstånd, kommer astronomen att se flera förvrängda bilder av objektet. Sådana effekter är kända som gravitationell linsverkan.[100] Beroende på konfiguration, skala och massfördelning, kan det finnas två eller flera bilder, en ljus ring kallas för Einsteinring och partiella ringar kallas för bågar.[101] Det tidigaste exemplet upptäcktes 1979;[102] sedan dess har mer än hundra gravitationslinser observerats.[103] Även om de multipla bilderna är för nära varandra för att kunna särskiljas, kan effekten fortfarande mätas, exempelvis som en total ljusning av målobjektet; ett antal sådana ”mikrolinseffekter” har observerats.[104]
Gravitationslinser har utvecklats till ett verktyg inom observationell astronomi. De används för att detektera närvaron och fördelningen av mörk materia, och ger ett ”naturligt teleskop” för att observera avlägsna galaxer och för att få en oberoende uppskattning av Hubblekonstanten. Statistiska utvärderingar av linsdata ger värdefulla insikter i hur galaxers struktur utvecklas.[105]
Gravitationsastronomi[redigera | redigera wikitext]
Observationer av binära pulsarer ger starka indirekta bevis för existensen av gravitationsvågor (se orbitala störningar ovan). Detektion av dessa vågor är ett viktigt mål för aktuell relativitetsrelaterad forskning.[106] Flera landbaserade gravitationsvågsdetektorer är för närvarande i drift, främst de interferometriska detektorerna GEO600, LIGO (två detektorer), TAMA 300 och Virgo.[107] Olika pulsartidsmatriser använder millisekundspulsarer för att upptäckta gravitationsvågor i frekvensområdet 10−9 till 10−8 Hertz (Hz), vilka härrör från binära supermassiva svarta hål.[75] Den europeiska rymdbaserade detektorn, LISA, är för närvarande under utveckling,[108] med ett inledande uppdrag (LISA Pathfinder) som sköts upp i december 2015.[109]
Observationer av gravitationsvågor kan komma att komplettera iakttagelser inom det elektromagnetiska spektrumet.[110] De förväntas ge information om svarta hål och andra täta föremål såsom neutronstjärnor och vita dvärgar, om vissa typer av supernovaimplosioner och om mycket tidiga processer i universum, inklusive signaturen av vissa typer av hypotetiska kosmiska strängar.[111] I februari 2016 meddelade Advanced LIGO-teamet att de hade detekterat gravitationsvågor från en sammanslagning av svarta hål.[72][73][112]
Svarta hål och andra kompakta objekt[redigera | redigera wikitext]
När förhållandet mellan ett föremåls massa och dess radie blir tillräckligt stort förutsäger allmänna relativitetsteorin bildandet av ett svart hål, en region i rymden från vilket ingenting, inte ens ljus, kan undkomma. I den för närvarande accepterade modellen av stjärnutveckling är neutronstjärnor omkring 1,4 solmassor och svarta hål med ett par till ett tiotal solmassor, det slutliga tillståndet för utvecklingen av massiva stjärnor.[113] Vanligtvis har en galax ett supermassivt svart hål med ett par miljoner till ett par miljarder solmassor i sitt centrum[114] och dess närvaro tros ha spelat en viktig roll i bildandet av galaxen och större kosmiska strukturer.[115]
Astronomiskt är den viktigaste egenskapen hos kompakta objekt att de ger en överlägset effektiv mekanism för omvandling av gravitationsenergi till elektromagnetisk strålning.[116] Ackretion, infallande damm och gasformigt material till massiva eller supermassiva svarta hål, tros orsaka några spektakulära lysande astronomiska objekt, särskilt olika typer av aktiva galaxkärnor på galaktiska skalor och stora stellära objekt såsom mikrokvasarer.[117] I synnerhet kan anhopning leda till relativistiska jetstrålar, fokuserade strålar av högenergetiska partiklar som slungas ut i rymden med nästan ljusets hastighet.[118] Allmänna relativitetsteorin spelar en central roll för att modellera alla dessa fenomen[119] och observationer ger starka belägg för existensen av svarta hål med de egenskaper som förutsägs av teorin.[120]
Svarta hål är också eftertraktade mål i sökandet efter gravitationsvågor (se gravitationsvågor ovan). Sammanslagning av binära svarta hål bör leda till att några av de starkaste gravitationella vågsignalerna når detektorerna på jorden och fasen direkt före fusionen skulle kunna användas för att härleda avståndet till fusionen (”kvitter”) och därmed fungera som en sond för kosmisk expansion vid stora avstånd.[121] De gravitationsvågor som produceras när ett svart hål med en stjärnas massa störtar in ett supermassivt svart hål, bör ge direkt information om det supertunga svarta hålets geometri.[122]
Kosmologi[redigera | redigera wikitext]

De nuvarande kosmologiska modellerna är baserade på Einsteins fältekvationer, vilka inkluderar den kosmologiska konstanten Λ eftersom den har ett viktigt inflytande på kosmos storskaliga dynamik:
där är rumtidsmetriken.[123] Isotropa och homogena lösningar till dessa förbättrade ekvationer, Friedmann–Lemaître–Robertson–Walkers lösningar,[124] tillåter fysiker att modellera ett universum som har utvecklats under de senaste 14 miljarder åren från en varm, tidig Big Bang-fas.[125] När ett litet antal parametrar (exempelvis universums materiemedeldensitet) har fastställts genom astronomiska observationer,[126] kan ytterligare observationsdata användas för att testa modeller.[127] Förutsägelser, alla framgångsrika, är bland annat den ursprungliga förekomsten av grundämnen bildade i en period av primordial nukleosyntes,[128] den storskaliga strukturen av universum,[129] och förekomsten och egenskaperna av ”värmeeko” från det tidiga kosmos, den kosmiska bakgrundsstrålningen.[130]
Astronomiska observationer av den kosmologiska expansionshastigheten tillåter att den totala mängden materia i universum kan uppskattas, även om materiens natur förblir en delvis gåtfull fråga. Omkring 90 % av all materia förefaller vara mörk materia, som har massa (eller, ekvivalent, gravitationsverkan), men inte växelverkar elektromagnetiskt och därmed inte kan observeras direkt.[131] Det finns ingen allmänt accepterad beskrivning av denna nya typ av materia inom ramen för känd partikelfysik[132] eller annorledes.[133] Observationer av avlägsna supernovors rödförskjutning och mätningar av den kosmiska bakgrundsstrålningen visar också att utvecklingen av vårt universum är påverkad av en kosmologisk konstant, som resulterar i en acceleration av kosmisk expansion eller, ekvivalent; av en energiform med ovanlig tillståndsekvation, känd som mörk energi, vars natur förblir oklar.[134]
En inflationsfas,[135] en fas av starkt accelererad expansion omkring 10−33 sekunder efter Big Bang, föreslogs 1980 för att förklara flera observationer, oförklarade av klassiska kosmologiska modeller, såsom den kosmiska bakgrundsstrålningens nästan perfekta homogenitet.[136] Nya mätningar av den kosmiska bakgrundsstrålningen har resulterat i det första beviset för detta scenario.[137] Det finns dock en förvillande mängd av möjliga inflationsscenarier som inte kan begränsas av aktuella observationer. Potentialfunktionen, som är avgörande för att bestämma inflationens dynamik, är helt enkelt postulerad, inte härledd från någon underliggande fysikalisk teori. En ännu större fråga är fysiken i det tidigaste universum, före inflationsfasen och precis efter där de klassiska modellerna förutsäger Big Bang-singularitet. Ett auktoritativt svar skulle kräva en fullständig teori om kvantgravitation, som ännu inte har utvecklats[138] (se avsnittet Kvantgravitation nedan).
Tidsresor[redigera | redigera wikitext]
Kurt Gödel visade[139] att det finns lösningar till Einsteins fältekvationer som innehåller slutna tidsliknande kurvor (Closed Timelike Circuits, CTC), vilka möjliggör tidsloopar. Lösningarna kräver extrema fysikaliska förutsättningar och det är osannolikt att de någonsin kommer att förekomma i praktiken. Det är fortfarande en öppen fråga huruvida andra fysiklagar kommer att eliminera dem helt. Sedan dess har andra – på liknande sätt opraktiska – lösningar som innehåller CTC hittats, till exempel Tiplercylindern och maskhål som skulle kunna användas som genvägar genom universum.
Avancerade begrepp[redigera | redigera wikitext]
Kausal struktur och global geometri[redigera | redigera wikitext]

I den allmänna relativitetsteorin kan ingen materiell kropp hinna ifatt en ljuspuls. Ingen påverkan från en händelse A kan nå någon annan plats X innan ljuset har hunnit färdas från A till X. Följaktligen ger en kartläggning av alla ljusvärldslinjer (nollgeodeter) viktig information om rumtidens kausala struktur. Denna struktur kan visas med hjälp av Penrose–Carter-diagram i vilka oändligt stora regioner av rummet och oändliga tidsintervall är förminskade (”kompaktifierade”) för att passa på en ändlig karta, medan ljuset fortfarande färdas längs diagonaler i standardrumtidsdiagram.[140]
Medveten om vikten av kausal struktur, utvecklade Roger Penrose och andra vad som är känt som global geometri. Inom global geometri är studieobjektet inte en enskild lösning (eller lösningsfamilj) till Einsteins ekvationer. Relationer som gäller för alla geodesier, såsom Raychaudhuriekvationen, och andra icke-specifika antaganden om materians natur (vanligtvis i form av energitillstånd) används snarare för att härleda allmänna resultat.[141]
Horisont[redigera | redigera wikitext]
Med hjälp av global geometri kan det visas att vissa rumtider innehåller händelsehorisonter som avgränsar en region från resten av rumtiden. De mest kända exemplen är svarta hål: om massa komprimeras till en tillräckligt kompakt region i rymden (såsom det är specificerat i ringkriteriet, är den relevanta längdskalan Schwarzschildradien[142]), kan ljus från insidan inte fly till utsidan. Eftersom inget objekt kan hinna ifatt en ljuspuls är all inre materia också infångad. Passage från utsidan till insidan är fortfarande möjlig, vilket visar att gränsen – det svarta hålets horisont – inte är en fysisk barriär.[143]

Vid tidiga studier av svarta hål förlitade man sig på explicita lösningar av Einsteins fältekvationer, i synnerhet den sfäriskt symmetriska Schwarzschildlösningen (som användes för att beskriva ett statiskt svart hål) och den axialsymmetriska Kerrmetriken (som användes för att beskriva ett roterande, stationärt svart hål, och introducerade intressanta särdrag såsom ergosfären). Med hjälp av global geometri, har senare studier visat mer allmänna egenskaper hos svarta hål. I det långa loppet, är de snarare ganska enkla objekt karaktäriserade av elva parametrar som specificerar energi, rörelsemängd, rörelsemängdsmoment, plats vid en specifik tidpunkt och elektrisk laddning. Detta framgår av svarta hålens entydighetssats: ”svarta hål har inget hår”, det vill säga inga kännetecken som frisyrer hos människor. Oberoende av komplexiteten hos det objekt som kollapsar för att bilda ett svart hål, är det resulterande objektet (med emitterade gravitationsvågor) mycket enkelt.[144]
Ännu mer anmärkningsvärt är att det finns en allmän uppsättning lagar, kända som svarta håls termodynamik, vilka är analoga med termodynamikens huvudsatser. Exempelvis, enligt andra lagen för svarta håls termodynamik, minskar arean av ett svart håls händelsehorisont aldrig med tiden, analogt med entropin hos ett termodynamiskt system. Detta begränsar den energi som kan extraheras genom klassiska medelvärden från ett roterande svart hål (exempelvis genom Penroseprocessen).[145] Det finns starka indikationer på att lagarna för svarta håls termodynamik i själva verket är en delmängd av termodynamikens huvudsatser och att det svarta hålets area är proportionell mot dess entropi.[146] Detta leder till en modifikation av lagarna för svarta hål: exempelvis, då andra lagen för svarta hål blir en del av termodynamikens andra huvudsats, är en minskning av ett svart håls area möjlig – så länge som andra processer ser till att den totala entropin ökar. Som termodynamiska objekt med nollskild temperatur bör svarta hål avge värmestrålning. Semiklassiska beräkningar indikerar att de faktiskt gör det och att ytgravitationen spelar temperaturens roll i Plancks strålningslag. Denna strålning är känd som Hawkingstrålning (se avsnittet Kvantfältteori i krökt rumtid nedan).[147]
Det finns andra typer av horisonter. I ett expanderande universum, bör en observatör upptäcka att vissa regioner i det förflutna kan observeras (”partikelhorisont”), och att vissa regioner i framtiden inte kan påverkas (händelsehorisont).[148] Även i ett platt Minkowskirum, när det beskrivs av en accelererande observatör (Rindlerrum), kommer det att finnas horisonter associerade med en semiklassisk strålning känd som Unruhstrålning.[149]
Singulariteter[redigera | redigera wikitext]
Ett annat allmänt drag i den allmänna relativitetsteorin är uppkomsten av rumtidsgränser kända som singulariteter. Rumtiden kan utforskas genom att följa tidsliknande och ljusliknande geodeter – alla möjliga sätt som ljus och partiklar i fritt fall kan färdas på. Några lösningar av Einsteins ekvationer har dock ”ojämna kanter” – regioner kända som gravitationella singulariteter eller rumtidssingulariteter, där ljusets och fallande partiklars vägar går mot ett abrupt slut och geometrin blir odefinierad. I de mer intressanta fallen är detta ”krökningssingulariteter” där geometriska storheter som kännetecknar rumtidskrökningen, som Ricciskalären, blir oändliga.[150] Välkända exempel på rumtider med framtida singulariteter – där världslinjer slutar – är Schwarzschildlösningen, vilken beskriver en singularitet inuti ett evigt statiskt svart hål,[151] och Kerrmetriken med sin ringformade singularitet inuti ett evigt roterande svart hål.[152] Friedmann–Lemaître–Robertson–Walkers lösningar och andra rumtider beskriver universum med tidigare singulariteter i vilka världslinjer börjar, nämligen Big Bang-singulariteter, och en del har likaså framtida singulariteter (Big Crunch).[153]
Givet att dessa exempel alla är mycket symmetriska – och därmed förenklade – är det frestande att dra slutsatsen att förekomsten av singulariteter är en artefakt av idealisering. Penrose–Hawkings singularitetssatser, bevisade med hjälp av den globala geometrins metoder, säger emellertid att singulariteter är ett generiskt inslag i den allmänna relativitetsteorin och oundvikliga när kollapsen av ett objekt med realistiska egenskaper har fortgått bortom ett visst stadium[154] och även i början av en vid klass av expanderande universum.[155] Satserna säger dock lite om singulariteternas egenskaper, och en stor del av aktuell forskning ägnas åt att karakterisera dessa objekts generiska struktur (en hypotetisk modell är Belinsky–Khalatnikov–Lifshitz-singularitet).[156] Den kosmiska censurförmodan säger att alla realistiska framtida singulariteter (inga perfekta symmetrier, utan materia med realistiska egenskaper) är gömda i säkerhet bakom en horisont, och därmed osynliga för alla avlägsna observatörer. Även om inga formella bevis ännu finns, stöder numeriska simuleringar dess giltighet.[157]
Evolutionsekvationer[redigera | redigera wikitext]
Varje lösning till Einsteins ekvation omfattar ett universums hela historia – det är inte enbart någon ögonblicksbild av hur det är, utan en hel, sannolikt materiefylld, rumtid. Den beskriver tillståndet av materia och geometri överallt och i varje moment i universumet ifråga. På grund av sin generella kovarians räcker inte Einsteins teori i sig för att bestämma tidsutvecklingen av den metriska tensorn. Den måste kombineras med ett koordinatvillkor, vilket är analogt med gaugefixering i andra fältteorier.[158]
För att förstå Einsteins ekvationer som partiella differentialekvationer, är det fördelaktigt att formulera dem på ett sätt som beskriver universums utveckling över tiden. Det görs i ”3 + 1”-formuleringar, där rumtiden är uppdelad i tre rumsdimensioner och en tidsdimension. Det mest kända exemplet är ADM-formalismen.[159] Dessa uppdelningar visar att evolutionsekvationerna för rumtiden i den allmänna relativitetsteorin beter sig väl: lösningar existerar alltid och är unikt definierade när lämpliga begynnelsevillkor har specificerats.[160] Sådana formuleringar av Einsteins fältekvationer utgör grunden för numerisk relativitetsteori.[161]
Globala och kvasilokala storheter[redigera | redigera wikitext]
Begreppet evolutionsekvation är intimt förbundet med en annan aspekt av allmän relativistisk fysik. I Einsteins teori visar det sig vara omöjligt att hitta en allmän definition av en till synes enkel egenskap som ett systems totala massa (eller energi). Huvudorsaken är att gravitationsfältet – liksom alla andra fysikaliska fält – måste tillskrivas en viss energi, men det visar sig vara fundamentalt omöjligt att lokalisera den energin.[162]
Det finns dock möjligheter att definiera ett systems totala massa, antingen med hjälp av en hypotetisk ”oändligt avlägsen observatör” (ADM-massa)[163] eller lämpliga symmetrier (Komarmassa).[164] Om man undantar från systemets totala massa den energi som överförs till oändligheten genom gravitationsvågor, blir resultatet Bondimassan vid nolloändlighet.[165] Precis som i klassisk fysik kan det visas att dessa massor är positiva.[166] Motsvarande globala definitioner finns för rörelsemängd och rörelsemängdsmoment.[167] Det har också förekommit en mängd försök att definiera kvasilokala kvantiteter, såsom massan av ett enskilt system uttryckt enbart med hjälp av storheter som definieras inom en ändlig region i rymden som innehåller detta system. Förhoppningen är att få en kvantitet användbar för allmänna uttalanden om isolerade system, såsom en mer exakt formulering av ringkriteriet.[168]
Förhållande till kvantteori[redigera | redigera wikitext]
Den allmänna relativitetsteorin betraktas som en av de två pelarna i den moderna fysiken, den andra är kvantteorin, grunden för förståelsen av materia från elementarpartiklar till fasta tillståndets fysik.[169] Hur kvantteorin kan förenas med den allmänna relativitetsteorin är dock fortfarande en öppen fråga.
Kvantfältteori i krökt rumtid[redigera | redigera wikitext]
De kvantfältteorier som utgör grunden för modern elementarpartikelfysik, definieras inom den speciella relativitetsteorin. Det är en utmärkt approximation när det gäller att beskriva beteendet hos mikroskopiska partiklar i de svaga gravitationsfält som förekommer på jorden.[170] För att beskriva situationer i vilka gravitationen är tillräckligt stark för att påverka (kvant)materia, men inte tillräckligt stark för själv behöva kvantiseras, har fysiker formulerat kvantfältteorier i krökt rumtid. Dessa teorier använder den allmänna relativitetsteorin för att definiera en krökt rumtid och använder sedan en generaliserad kvantfältteori för att beskriva beteendet hos kvantmateria inom den rumtiden.[171] Med användning av denna formalism, kan det visas att svarta hål avger ett svartkroppsspektrum av partiklar känd som Hawkingstrålning, vilket leder till möjligheten att de avdunstar med tiden.[172] Som kortfattat nämnts ovan spelar denna strålning en viktig roll för svarta håls termodynamik.[173]
Kvantgravitation[redigera | redigera wikitext]
Behovet av konsistens mellan en kvantbeskrivning av materia och en geometrisk beskrivning av rumtiden,[174] såväl som förekomsten av singulariteter (där krökningsradierna blir mikroskopiska), visar på behovet av en fullständig teori om kvantgravitation. För en adekvat beskrivning av svarta håls inre och det mycket tidiga universum behövs en teori i vilken gravitationen och den associerade rumtidsgeometrin beskrivs i termer av kvantmekanik.[175] Trots stora insatser finns det ännu ingen fullständig och konsistent teori om kvantgravitation, även om ett antal kandidater finns.[176][177]

Försök att generalisera vanliga kvantfältteorier, som används i elementarpartikelfysik för att beskriva fundamentala växelverkan, så att de omfattar gravitation har lett till allvarliga problem.[178] Vissa har hävdat att detta tillvägagångssätt kan vara framgångsrikt vid låga energier, eftersom det resulterar i en acceptabel effektiv (kvant)fältteori om gravitation.[179] Vid mycket höga energier är dock resultaten modeller som saknar all prognosförmåga (”icke-renormerbara”).[180]

Ett försök att övervinna dessa begränsningar är strängteori, en kvantteori som inte baseras på punktpartiklar, utan minimala endimensionella utvidgade objekt.[181] Teorin ser ut att bli en enhetlig beskrivning av alla partiklar och växelverkan, inklusive gravitation;[182] priset att betala är ovanliga egenskaper som sex extra rumsdimensioner utöver de vanliga tre.[183] I vad som kallas för den andra supersträngrevolutionen, förmodades både strängteori och en förening av den allmänna relativitetsteorin och supersymmetri, känt som supergravitation,[184] vilket lade grunden för en hypotetisk elvadimensionell modell känd som M-teori, vilket skulle utgöra en unikt definierad och konsistent teori om kvantgravitation.[185]
Ett annat tillvägagångssätt börjar med de kanoniska kvantiseringsprocedurerna för kvantteori. Med hjälp av initialvärdeformuleringen av den allmänna relativitetsteorin (se Evolutionsekvationer ovan), är resultatet Wheeler–DeWitts ekvation (en analogi till Schrödingerekvationen) som dessvärre är dåligt definierad.[186] Med införandet av det som nu är känt som Ashtekarvariabler,[187] leder dock detta till en lovande modell känd som loopkvantgravitation. Rummet representeras av en nätliknande struktur känd som spinn-nätverk, vilket utvecklas över tiden i diskreta steg.[188]
Beroende på vilka funktioner i den allmänna relativitetsteorin och kvantteorin som accepteras som oförändrade, och på vilken nivå förändringar introduceras,[189] finns det många andra försök att komma fram till en bärkraftig teori om kvantgravitation – några exempel är gittergravitationsteorin baserad på Feynmans vägintegralformulering och reggekalkyl,[176] dynamisk triangulering,[190] kausala mängder,[191] twistormodeller[192] eller vägintegralbaserade modeller av kvantkosmologi.[193]
Alla kandidatteorier har fortfarande stora formella och begreppsmässiga problem. De möter också det vanliga problemet att det, än så länge, inte finns något sätt att genomföra experimentella tester för förutsägelser om kvantgravitation (och därmed välja mellan kandidaterna där deras förutsägelser varierar), även om det finns hopp för att detta skall förändras i takt med att framtida data från kosmologiska observationer och partikelfysikexperiment blir tillgängliga.[194]
Aktuell status[redigera | redigera wikitext]
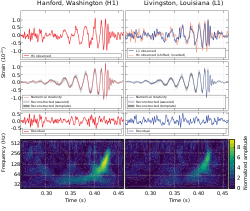
Allmänna relativitetsteorin har blivit en mycket framgångsrik modell för gravitation och kosmologi, som hittills har klarat många observationella och experimentella tester. Det finns dock starka indikationer på att teorin är ofullständig.[195] Problemet med kvantgravitationen och frågan om rumtidssingulariteters realitet förblir öppna, se avsnittet Kvantgravitation ovan. Observationer som tas som bevis för mörk energi och mörk materia kan indikera behovet av en ny fysik, se avsnittet Kosmologi ovan. Även om den tas som den är, är allmänna relativitetsteorin rik på möjligheter för ytterligare utforskning. Matematiker försöker förstå singulariteters natur och de grundläggande egenskaperna hos Einsteins ekvationer,[196] och alltmer kraftfulla datorsimuleringar körs (exempelvis för ekvationerna som beskriver sammanslagning av svarta hål).[197] I februari 2016 meddelades det att gravitationsvågor hade detekterats av Advanced LIGO-teamet den 14 september 2015.[198][199] Ett sekel efter offentliggörandet, är den allmänna relativitetsteorin fortfarande ett mycket aktivt forskningsområde.[200]
Referenser[redigera | redigera wikitext]
Noter[redigera | redigera wikitext]
- ^ O'Connor, J.J.; Robertson, E.F. (maj 1996). ”General Relativity”. MacTutor History of Mathematics archive. University of St. Andrews. https://mathshistory.st-andrews.ac.uk/HistTopics/General_relativity/. Läst 16 juni 2022.
- ^ Pais 1982, kap. 9–15; Renn 2007 innehåller artiklar om aktuell forskning, inklusive nytryck av många av de ursprungliga artiklarna; en tillgänglig översikt finns i Renn 2005, s. 110ff. Einsteins originalverk finns i Digital Einstein, volym 4 och 6. En tidig nyckelartikel är Einstein 1907, se Pais 1982, kap. 9. Artikeln som introducerar fältekvationerna är Einstein 1915, se Pais 1982, kap. 11–15.
- ^ Schwarzschild 1916a, Schwarzschild 1916b. och Reissner 1916. (senare kompletterad i Nordström 1918.)
- ^ Einstein 1917, se Pais 1982, kap. 15e.
- ^ Hubbles ursprungliga artikel är Hubble 1929; en tillgänglig översikt ges i Singh 2004, kap. 2–4.
- ^ Rapporterades i Gamow 1970.
- ^ Pais 1982, s. 253–254.
- ^ Kennefick 2005, Kennefick 2007.
- ^ Pais 1982, kap. 16.
- ^ Thorne, Kip (2003). ”Warping spacetime”. The future of theoretical physics and cosmology: celebrating Stephen Hawking's 60th birthday. Cambridge University Press. sid. 74. ISBN 0-521-82081-2. https://books.google.com/books?id=yLy4b61rfPwC, Extract of page 74
- ^ Israel 1987, kap. 7.8–7.10, Thorne 1994, kap. 3–9.
- ^ Avsnitten Baneffekter och riktningens relativitet, Gravitationell tidsdilatation och frekvensskift och Ljusets böjning och gravitationell tidsfördröjning, och referenser däri.
- ^ Avsnittet Kosmologi och referenser däri; den historiska utvecklingen finns beskriven i Overbye 1999.
- ^ Redogörelsen följer här motsvarande avsnitt i Ehlers 1973, avsnitt 1.
- ^ Arnold 1989, kap. 1.
- ^ Ehlers 1973, s. 5f.
- ^ Will 1993, avsnitt 2.4, Will 2014, avsnitt 2.1.
- ^ Wheeler 1990, kap. 2.
- ^ Ehlers 1973, avsnitt 1.2, Havas 1964, Künzle 1972. Detta enkla tankeexperiment beskrevs först i Heckmann & Schücking 1959.
- ^ Ehlers 1973, s. 10f.
- ^ Bra introduktioner är – i ordning efter ökande förkunskaper i matematik – Giulini 2005, Mermin 2005. och Rindler 1991; för redogörelser av precisionsexperiment, se del IV av Ehlers & Lämmerzahl 2006.
- ^ En djupgående jämförelse mellan de två symmetrigrupperna finns i Giulini 2006a.
- ^ Rindler 1991, avsnitt 22, Synge 1972, kap. 1 och 2.
- ^ Ehlers 1973, avsnitt 2.3.
- ^ Ehlers 1973, avsnitt 1.4, Schutz 1985, avsnitt 5.1.
- ^ Ehlers 1973, s. 17ff; en härledning finns i Mermin 2005, kap. 12. För experimentella bevis, se avsnittet Gravitationell tidsdilatation och frekvensskift nedan.
- ^ Rindler 2001, avsnitt 1.13; för en grundläggande redogörelse, se Wheeler 1990, kap. 2; det finns dock vissa skillnader mellan den moderna versionen och Einsteins ursprungliga begrepp som användes i den historiska härledningen av den allmänna relativitetsteorin, se Norton 1985.
- ^ Ehlers 1973, avsnitt 1.4; för det experimentella beviset, se ännu en gång avsnittet Gravitationell tidsdilatation och frekvensskift. Att använda en annan förbindelse med torsion skild från noll leder till en modifierad teori känd som Einstein–Cartans teori.
- ^ Ehlers 1973, s. 16, Kenyon 1990, avsnitt 7.2, Weinberg 1972, avsnitt 2.8.
- ^ Ehlers 1973, s. 19–22; för liknande härledningar, se avsnitten 1 och 2 i kap. 7 i Weinberg 1972.
- ^ Lovelock 1972.
- ^ Schutz 1985, avsnitt 8.3.
- ^ Kenyon 1990, avsnitt 7.4.
- ^ Brans & Dicke 1961, Weinberg 1972, avsnitt 3 i kap. 7, Goenner 2004, avsnitt 7.2. och Trautman 2006.
- ^ Wald 1984, kap. 4, Weinberg 1972, kap. 7. eller egentligen alla läroböcker i allmänna relativitetsteorin.
- ^ Åtminstone approximativt, se Poisson 2004.
- ^ Wheeler 1990, s. xi.
- ^ Wald 1984, avsnitt 4.4.
- ^ Wald 1984, avsnitt 4.1.
- ^ För (de konceptuella och historiska) svårigheterna med att definiera en allmän princip om relativitet och separera den från begreppet allmän kovarians, se Giulini 2006b.
- ^ Avsnitt 5 i kap. 12 i Weinberg 1972.
- ^ De inledande kapitlen i Stephani et al. 2003.
- ^ En genomgång av Einsteins ekvation i ett bredare sammanhang tillsammans med andra partiella differentialekvationer med fysikalisk betydelse är Geroch 1996.
- ^ För bakgrundsinformation och en lista över lösningar, se Stephani et al. 2003; en färskare översikt finns i MacCallum 2006.
- ^ Chandrasekhar 1983, kap. 3,5,6.
- ^ Narlikar 1993, kap. 4, avsnitt 3.3.
- ^ Kortfattade beskrivningar av dessa och ytterligare intressanta lösningar finns i Hawking & Ellis 1973, kap. 5.
- ^ Lehner 2002.
- ^ Se till exempel Wald 1984, avsnitt 4.4.
- ^ Will 1993, avsnitt 4.1 och 4.2.
- ^ Will 2014, avsnitt 3.2, Will 1993, kap. 4.
- ^ Rindler 2001, s. 24–26 versus s. 236–237. och Ohanian & Ruffini 1994, s. 164–172. Einstein härledde dessa effekter genom att använda ekvivalensprincipen så tidigt som 1907, se Einstein 1907. och beskrivningen i Pais 1982, s. 196–198.
- ^ Rindler 2001, s. 24–26; Misner, Thorne & Wheeler 1973, § 38.5.
- ^ Pound–Rebka-experimentet, se Pound & Rebka 1959, Pound & Rebka 1960; Pound & Snider 1964; en lista över ytterligare experiment finns i Ohanian & Ruffini 1994, table 4.1 on p. 186.
- ^ Greenstein, Oke & Shipman 1971; de senaste och mest exakta Sirius B-mätningarna är publicerade i Barstow, Bond et al. 2005.
- ^ Med början i Hafele–Keating-experimentet, Hafele & Keating 1972a. och Hafele & Keating 1972b, och kulmen i Gravity Probe A-experimentet, finns en experimentöversikt i Ohanian & Ruffini 1994, tabell 4.1 på s. 186.
- ^ GPS testas kontinuerligt genom att jämföra atomklockor på marken och ombord satelliter i omloppsbanan; för en redogörelse av relativistiska effekter, se Ashby 2002. och Ashby 2003.
- ^ Stairs 2003. och Kramer 2004.
- ^ Allmänna översikter finns i Will 2014, avsnitt 2.1; Ohanian & Ruffini 1994, avsnitt 4.2.
- ^ Ohanian & Ruffini 1994, s. 164–172.
- ^ Se Kennefick 2005. för de klassiska tidiga mätningarna från Eddingtons forskningsresor; för en översikt av senare mätningar, se Ohanian & Ruffini 1994, kap. 4.3. För de mest exakta direkta moderna observationerna som använder sig av kvasarer, se Shapiro et al. 2004.
- ^ Detta är inte ett oberoende axiom; det kan härledas från Einsteins ekvationer och den maxwellska lagrangefunktionen genom att använda WKB-approximationen, se Ehlers 1973, avsnitt 5.
- ^ Blanchet 2014, avsnitt 1.4.
- ^ Rindler 2001, avsnitt 1.16; för de historiska exemplen, Israel 1987, s. 202–204; i själva verket publicerade Einstein en sådan härledning i Einstein 1907. Sådana beräkningar antar underförstått att rummets geometri är euklidiskt, se Ehlers & Rindler 1997.
- ^ Med utgångspunkt från Einsteins teori, tar dessa härledningar hänsyn till inverkan av gravitation i tiden, men inte dess konsekvenser för förvrängning av rummet, se Rindler 2001, avsnitt 11.11.
- ^ För solens gravitationsfält reflekterat från planeter såsom Venus och Merkurius med hjälp av radarsignaler, se Shapiro 1964, Weinberg 1972, kap. 8, avsnitt 7; för signaler som aktivt tillbakaskickas av rymdsonder (transpondermätningar), se Bertotti, Iess & Tortora 2003; för en översikt, se Ohanian & Ruffini 1994, tabell 4.4 på s. 200; för senare mätningar med signaler som mottas från en pulsar som är en del av ett binärt system, är gravitationsfältet som orsakar tidsfördröjningen den andra pulsaren, se Stairs 2003, avsnitt 4.4.
- ^ Will 1993, avsnitt 7.1 och 7.2.
- ^ Einstein, A (Juni 1916). ”Näherungsweise Integration der Feldgleichungen der Gravitation”. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin del 1: sid. 688–696. Arkiverad från originalet den 21 mars 2019. https://web.archive.org/web/20190321062928/http://einstein-annalen.mpiwg-berlin.mpg.de/related_texts/sitzungsberichte. Läst 16 april 2016.
- ^ Einstein, A (1918). ”Über Gravitationswellen”. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin del 1: sid. 154–167. Arkiverad från originalet den 21 mars 2019. https://web.archive.org/web/20190321062928/http://einstein-annalen.mpiwg-berlin.mpg.de/related_texts/sitzungsberichte. Läst 16 april 2016.
- ^ De flesta avancerade läroböcker i allmän relativitetsteori innehåller en beskrivning av dessa egenskaper, exempelvis Schutz 1985, kap. 9.
- ^ Nobelprize.org, Nobelpriset i fysik 1993
- ^ [a b] Castelvecchi, Davide; Witze (11 februari 2016). ”Einstein's gravitational waves found at last”. Nature News. doi:. http://www.nature.com/news/einstein-s-gravitational-waves-found-at-last-1.19361.
- ^ [a b] B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) (11 februari 2016). ”Observation of Gravitational Waves from a Binary Black Hole Merger”. Physical Review Letters 116 (6). doi:. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.061102.
- ^ ”Gravitational waves detected 100 years after Einstein's prediction | NSF - National Science Foundation”. http://www.nsf.gov/news/news_summ.jsp?cntn_id=137628. Läst 11 februari 2016.
- ^ [a b] G. Hobbs et. al. (2010). ”The international pulsar timing array project: using pulsars as a gravitational wave detector”. Classical and Quantum Gravity 27 (8): sid. 084013. doi:. https://arxiv.org/abs/0911.5206.
- ^ Exempelvis Jaranowski & Królak 2005.
- ^ Rindler 2001, kap. 13.
- ^ Gowdy 1971, Gowdy 1974.
- ^ Se Lehner 2002. för en kort introduktion till den numeriska relativitetsteorins metoder, och Seidel 1998. för kopplingen till gravitationsastronomi.
- ^ Schutz 2003, s. 48–49, Pais 1982, s. 253–254.
- ^ Rindler 2001, avsnitt 11.9.
- ^ Will 1993, s. 177–181.
- ^ Följaktligen, i parametriserad postnewtonsk formalism (PPN), bestämmer mätningar av denna effekt en linjär kombination av termerna ß och γ, se Will 2014, avsnitt 4.2. och Will 1993, avsnitt 7.3.
- ^ De mest exakta mätningarna är långbasinterferometriska mätningar av planetpositioner; se Will 1993, kap. 5, Will 2014, avsnitt 4.2, Anderson et al. 1992; för en översikt, Ohanian & Ruffini 1994, s. 406–407.
- ^ Kramer et al. 2006.
- ^ En bild som inkluderar felstaplar finns i Will 2014, avsnitt 6.1, figur 7.
- ^ Stairs 2003, Schutz 2003, s. 317–321, Bartusiak 2000, s. 70–86.
- ^ Weisberg & Taylor 2003; för upptäckten av pulsaren, se Hulse & Taylor 1975; för det första beviset för gravitationsstrålning, se Taylor 1994.
- ^ Kramer 2004.
- ^ Penrose 2004, §14.5, Misner, Thorne & Wheeler 1973, §11.4.
- ^ Weinberg 1972, avsnitt 9.6, Ohanian & Ruffini 1994, avsnitt 7.8.
- ^ Bertotti, Ciufolini & Bender 1987, Nordtvedt 2003.
- ^ Kahn 2007.
- ^ En uppdragsbeskrivning återfinns i Everitt et al. 2001; en första utvärdering efter flygningen ges i Everitt, Parkinson & Kahn 2007; ytterligare uppdateringar kommer att finnas tillgängliga på uppdragets webbplats Kahn 1996–2012.
- ^ Townsend 1997, avsnitt 4.2.1, Ohanian & Ruffini 1994, s. 469–471.
- ^ Ohanian & Ruffini 1994, avsnitt 4.7, Weinberg 1972, avsnitt 9.7; för en senare översikt, se Schäfer 2004.
- ^ Ciufolini & Pavlis 2004, Ciufolini, Pavlis & Peron 2006, Iorio 2009.
- ^ Iorio L. (augusti 2006). ”COMMENTS, REPLIES AND NOTES: A note on the evidence of the gravitomagnetic field of Mars” (på engelska). Classical Quantum Gravity 23 (17): sid. 5451–5454. doi:. https://arxiv.org/abs/gr-qc/0606092.
- ^ Iorio L. (juni 2010). ”On the Lense–Thirring test with the Mars Global Surveyor in the gravitational field of Mars” (på engelska). Central European Journal of Physics 8 (3): sid. 509–513. doi:. https://arxiv.org/abs/gr-qc/0701146.
- ^ För översikter av gravitationell linsverkan och dess tillämpningar, se Ehlers, Falco & Schneider 1992. och Wambsganss 1998.
- ^ För en enkel härledning, se Schutz 2003, kap. 23; se Narayan & Bartelmann 1997, avsnitt 3.
- ^ Walsh, Carswell & Weymann 1979.
- ^ Bilder av alla kända linser återfinns på CASTLES-projektets sidor, Kochanek et al. 2007.
- ^ Roulet & Mollerach 1997.
- ^ Narayan & Bartelmann 1997, avsnitt 3.7.
- ^ Barish 2005, Bartusiak 2000, Blair & McNamara 1997.
- ^ Hough & Rowan 2000.
- ^ Danzmann & Rüdiger 2003.
- ^ ”LISA pathfinder overview” (på engelska). ESA. http://www.esa.int/esaSC/120397_index_0_m.html. Läst 23 april 2012.
- ^ Thorne 1995.
- ^ Cutler & Thorne 2002.
- ^ ”Gravitational waves detected 100 years after Einstein's prediction | NSF - National Science Foundation”. www.nsf.gov. http://www.nsf.gov/news/news_summ.jsp?cntn_id=137628. Läst 11 februari 2016.
- ^ Miller 2002, föreläsning 19 och 21.
- ^ Celotti, Miller & Sciama 1999, avsnitt 3.
- ^ Springel et al. 2005. och den åtföljande sammanfattningen Gnedin 2005.
- ^ Blandford 1987, avsnitt 8.2.4.
- ^ För den grundläggande mekanismen, se Carroll & Ostlie 1996, avsnitt 17.2; för mer information om de olika typerna av astronomiska objekt som är associerade med den, se Robson 1996.
- ^ För en översikt, se Begelman, Blandford & Rees 1984. Till en avlägsen observatör förefaller dessa strålar att röra sig snabbare än ljuset; detta kan dock förklaras som en optisk illusion som inte bryter mot principerna i relativitetsteorin, se Rees 1966.
- ^ För stellära sluttillstånd, se Oppenheimer & Snyder 1939. eller, för senare numeriskt arbete, Font 2003, avsnitt 4.1; för supernovor finns det fortfarande stora problem som måste lösas, se Buras et al. 2003; för simulering av ackretionen och bildandet av jetstrålar, se Font 2003, avsnitt 4.2. Dessutom antas relativistiska linseffekter spela en roll för signalerna som mottas från röntgenpulsarer, se Kraus 1998.
- ^ Det går att dra slutsatser om hur kompakt ett objekt är från observation av ackretionsfenomen ("Eddington-luminositet"), se Celotti, Miller & Sciama 1999; observationer av stjärnors rörelse nära Vintergatans centrum, se Schödel et al. 2003, och indikationer på att åtminstone vissa av de kompakta objekten tycks sakna fast yta, vilket man kan sluta sig till från observation av röntgenblixtar för vilka det centrala kompakta objektet antingen är en neutronstjärna eller ett svart hål; se Remillard et al. 2006. för en översikt, Narayan 2006, avsnitt 5. Försök har också gjorts att observera "skuggan" av horisonten av det svarta hålet i Vintergatans centrum, se Falcke, Melia & Agol 2000.
- ^ Dalal et al. 2006.
- ^ Barack & Cutler 2004.
- ^ Ursprungligen Einstein 1917; se Pais 1982, s. 285–288.
- ^ Carroll 2001, kap. 2.
- ^ Bergström & Goobar 2003, kap. 9–11; användning av dessa modeller motiveras av det faktum att vid stora skalor på cirka hundra miljoner ljusår och mer, verkar faktiskt vårt eget universum vara isotropt och homogent, se Peebles et al. 1991.
- ^ Exempelvis med WMAP-data, se Spergel et al. 2003.
- ^ Dessa tester involverar olika observationer som beskrivs längre fram, se exempelvis figur 2 i Bridle et al. 2003.
- ^ Peebles 1966; för en senare redogörelse av förutsägelser, se Coc, Vangioni‐Flam et al. 2004; en tillgänglig redogörelse finns i Weiss 2006; jämför med observationerna i Olive & Skillman 2004, Bania, Rood & Balser 2002, O'Meara et al. 2001. och Charbonnel & Primas 2005.
- ^ Lahav & Suto 2004, Bertschinger 1998, Springel et al. 2005.
- ^ Alpher & Herman 1948, för en pedagogisk introduktion, se Bergström & Goobar 2003, kap. 11; för den inledande detektionen, se Penzias & Wilson 1965. och, för precisionsmätningar av satellitobservatorier, Mather et al. 1994. (COBE) och Bennett et al. 2003. (WMAP). Framtida mätningar kan också avslöja bevis om gravitationsvågor i det tidiga universum; denna kompletterande information återfinns i bakgrundsstrålningens polarisation, se Kamionkowski, Kosowsky & Stebbins 1997. och Seljak & Zaldarriaga 1997.
- ^ Bevis för detta kommer från bestämningen av kosmologiska parametrar och ytterligare observationer som inbegriper dynamiken i galaxer och galaxhopar, se Peebles 1993, kap. 18, för bevis från gravitationell linsverkan, se Peacock 1999, avsnitt 4.6, och för simuleringar av bildande av storskaliga strukturer, se Springel et al. 2005.
- ^ Peacock 1999, kap. 12, Peskin 2007; i synnerhet antyder observationer att endast en försumbar del av denna materia är i form av vanliga elementarpartiklar (”baryonisk materia”), se Peacock 1999, kap. 12.
- ^ Vissa fysiker har ifrågasatt huruvida bevis för mörk materia i själva verket är bevis för avvikelser från den einsteinska (och newtonska) beskrivningen av gravitation, se översikten i Mannheim 2006, avsnitt 9.
- ^ Carroll 2001; en tillgänglig översikt finns i Caldwell 2004. Även här har forskare hävdat att bevisningen inte antyder en ny form av energi, men däremot behovet av ändringar i våra kosmologiska modeller, se Mannheim 2006, avsnitt 10; ovannämnda ändringar behöver inte vara ändringar av den allmänna relativitetsteorin, de kan exempelvis vara modifikationer i hur vi behandlar inhomogeniteter i universum, se Buchert 2007.
- ^ En bra introduktion är Linde 1990; för en mer aktuell genomgång, se Linde 2005.
- ^ Mer precist är dessa planhetsproblemet, horisontproblemet och monopolproblemet; en pedagogisk introduktion finns i Narlikar 1993, avsnitt 6.4, se även Börner 1993, avsnitt 9.1.
- ^ Spergel et al. 2007, avsnitt 5,6.
- ^ Brandenberger 2007, avsnitt 2.
- ^ Gödel 1949.
- ^ Frauendiener 2004, Wald 1984, avsnitt 11.1, Hawking & Ellis 1973, avsnitt 6.8, 6.9.
- ^ Wald 1984, avsnitt 9.2–9.4. och Hawking & Ellis 1973, kap. 6.
- ^ Thorne 1972; för nyare numeriska studier, se Berger 2002, avsnitt 2.1.
- ^ Israel 1987. En mer exakt matematisk beskrivning skiljer på flera typer av horisonter, särskilt händelsehorisonter och skenbara horisonter, se Hawking & Ellis 1973, s. 312–320. eller Wald 1984, avsnitt 12.2; det finns också mer intuitiva definitioner för isolerade system som inte kräver kunskap om rumtidsegenskaper vid oändligheten, se Ashtekar & Krishnan 2004.
- ^ För de första stegen, se Israel 1971; se Hawking & Ellis 1973, avsnitt 9.3. eller Heusler 1996, kap. 9 och 10. för en härledning, och Heusler 1998. såväl som Beig & Chruściel 2006. för översikter över mer aktuella resultat.
- ^ Lagarna för svarta håls termodynamik beskrevs först i Bardeen, Carter & Hawking 1973; en mer pedagogisk presentation finns i Carter 1979; för en mer aktuell genomgång, se Wald 2001, kap. 2. En grundlig introduktion, inklusive en introduktion till den nödvändiga matematiken finns i Poisson 2004. För Penroseprocessen, se Penrose 1969.
- ^ Bekenstein 1973, Bekenstein 1974.
- ^ Faktumet att svarta hål avger strålning, kvantmekaniskt, härleddes först i Hawking 1975; en mer noggrann härledning finns i Wald 1975. En genomgång ges också i Wald 2001, kap. 3.
- ^ Narlikar 1993, avsnitt 4.4.4, 4.4.5.
- ^ Horisonter: se Rindler 2001, avsnitt 12.4. Unruh-effekten: Unruh 1976, även Wald 2001, kap. 3.
- ^ Hawking & Ellis 1973, avsnitt 8.1, Wald 1984, avsnitt 9.1.
- ^ Townsend 1997, kap. 2; en mer omfattande behandling av denna lösning finns i Chandrasekhar 1983, kap. 3.
- ^ Townsend 1997, kap. 4; för en mer omfattande behandling, se Chandrasekhar 1983, kap. 6.
- ^ Ellis & Van Elst 1999; en närmare titt på singulariteten i sig tas i Börner 1993, avsnitt 1.2.
- ^ Nämligen när det finns fångade nollytor, se Penrose 1965.
- ^ Hawking 1966.
- ^ Förmodandet gjordes i Belinskii, Khalatnikov & Lifschitz 1971; för en mer aktuell genomgång, se Berger 2002. En tillgänglig utläggning ges av Garfinkle 2007.
- ^ Begränsningen till framtida singulariteter utesluter naturligtvis initiala singulariteter som Big Bang-singulariteten, som i princip är synlig för observatörer vid senare kosmisk tid. Den kosmiska censurförmodan presenterades först i Penrose 1969; en redogörelse på läroboksnivå ges i Wald 1984, s. 302–305. För numeriska resultat, se genomgången Berger 2002, avsnitt 2.1.
- ^ Hawking & Ellis 1973, avsnitt 7.1.
- ^ Arnowitt, Deser & Misner 1962; för en pedagogisk introduktion, se Misner, Thorne & Wheeler 1973, §21.4–§21.7.
- ^ Fourès-Bruhat 1952. och Bruhat 1962; för en pedagogisk introduktion, se Wald 1984, kap. 10; en onlineredogörelse finns i Reula 1998.
- ^ Gourgoulhon 2007; för en översikt över grunderna för numerisk relativitetsteori, inklusive de problem som uppstår på grund av säregenheterna hos Einsteins ekvationer, se Lehner 2001.
- ^ Misner, Thorne & Wheeler 1973, §20.4.
- ^ Arnowitt, Deser & Misner 1962.
- ^ Komar 1959; för en pedagogisk introduktion, se Wald 1984, avsnitt 11.2; fastän definierad på ett helt annat sätt, kan det visas att Komarmassan är ekvivalent med ADM-massan för stationära rumtider, se Ashtekar & Magnon-Ashtekar 1979.
- ^ För en pedagogisk introduktion, se Wald 1984, avsnitt 11.2.
- ^ Wald 1984, s. 295 och referenser däri; detta är viktigt för stabilitetsfrågor – om det fanns tillstånd med negativ massa, så skulle det platta, tomma Minkowskirummet, som har nollmassa, kunna utvecklas till dessa tillstånd
- ^ Townsend 1997, kap. 5.
- ^ Sådana kvasilokala massenergidefinitioner är Hawkingenergin, Gerochenergin eller Penroses kvasilokala energirörelsemängd baserad på twistorteoretiska metoder; se översiktsartikeln Szabados 2004.
- ^ En översikt över kvantteori finns i standardläroböcker som Messiah 1999; en mer grundläggande redogörelse ges i Hey & Walters 2003.
- ^ Weinberg 1995, Peskin & Schroeder 1995; en mer tillgänglig översikt är Auyang 1995.
- ^ Wald 1994, Birrell & Davies 1984.
- ^ För Hawkingstrålning Hawking 1975, Wald 1975; en tillgänglig introduktion till avdunstning av svarta hål finns i Traschen 2000.
- ^ Wald 2001, kap. 3.
- ^ Enkelt uttryckt är materia källan till rumtidskrökning, och när materia har kvantegenskaper kan vi förvänta oss att rumtiden också har dem. se Carlip 2001, avsnitt 2.
- ^ Schutz 2003, s. 407.
- ^ [a b] Hamber 2009.
- ^ En tidslinje och översikt finns i Rovelli 2000.
- ^ 't Hooft 1974.
- ^ Donoghue 1995.
- ^ I synnerhet en perturbativ teknik känd som renormering, en integrerad del av härledda förutsägelser som tar hänsyn till högre energibidrag, se Weinberg 1996, ch. 17, 18, vilket misslyckas i detta fall; se Veltman 1975, Goroff & Sagnotti 1985; för en nyligen omfattande granskning av misslyckandet av perturbativ renormeringsbarhet för kvantgravitation, se Hamber 2009.
- ^ En tillgänglig introduktion på grundnivå finns i Zwiebach 2004; mer fullständiga översikter finns i Polchinski 1998a. och Polchinski 1998b.
- ^ Vid energierna som nås i aktuella experiment är dessa strängar oskiljbara från punktliknande partiklar, men skiljer sig väsentligt från normalmodus av oscillation av en och samma typ av fundamental sträng som framträder som partiklar med olika (elektriska och andra) laddningar, exempelvis Ibanez 2000. Teorin är framgångsrik i det att ett modus alltid kommer att motsvara en graviton, gravitationens fältpartikel, exempelvis Green, Schwarz & Witten 1987, avsnitt 2.3, 5.3.
- ^ Green, Schwarz & Witten 1987, avsnitt 4.2.
- ^ Weinberg 2000, kap. 31.
- ^ Townsend 1996, Duff 1996.
- ^ Kuchar 1973, avsnitt 3.
- ^ Dessa variabler representerar geometrisk gravitation med hjälp av matematiska analoger av elektriska fält och magnetfält; se Ashtekar 1986, Ashtekar 1987.
- ^ För en genomgång, se Thiemann 2006; mer omfattande redogörelser finns i Rovelli 1998, Ashtekar & Lewandowski 2004. såväl som i föreläsningsanteckningarna Thiemann 2003.
- ^ Isham 1994, Sorkin 1997.
- ^ Loll 1998.
- ^ Sorkin 2005.
- ^ Penrose 2004, kap. 33 och referenser däri.
- ^ Hawking 1987.
- ^ Ashtekar 2007, Schwarz 2007.
- ^ Maddox 1998, s. 52–59, 98–122; Penrose 2004, avsnitt 34.1, kap. 30.
- ^ Friedrich 2005.
- ^ För en genomgång av de olika problemen och teknikerna som utvecklats för att övervinna dem, se Lehner 2002.
- ^ Färsk information finns på de stora detektorprojektens webbplatser, se under Externa länkar
- ^ För artiklar om polariserade gravitationsvågor från kompakta binärer, se Blanchet et al. 2008. och Arun et al. 2007; för en översikt över forskningen om kompakta binärer, se Blanchet 2014. och Futamase & Itoh 2006; för en översikt över experimentella tester av allmän relativitetsteori, se Will 2014.
- ^ Se exempelvis den fackgranskade elektroniska tidskriften Living Reviews in Relativity
Källor[redigera | redigera wikitext]
- Alpher, R. A.; Herman, R. C. (1948). ”Evolution of the universe”. Nature 162 (4124): sid. 774–775. doi:.
- Anderson, J. D.; Campbell, J. K.; Jurgens, R. F.; Lau, E. L. (1992). ”Recent developments in solar-system tests of general relativity”. i Sato, H.; Nakamura, T.. Proceedings of the Sixth Marcel Großmann Meeting on General Relativity. World Scientific. sid. 353–355. ISBN 981-02-0950-9
- Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics. Springer. ISBN 3-540-96890-3
- Arnowitt, Richard; Deser, Stanley; Misner, Charles W. (1962). ”The dynamics of general relativity”. i Witten, Louis. Gravitation: An Introduction to Current Research. Wiley. sid. 227–265. https://arxiv.org/pdf/gr-qc/0405109.pdf
- Arun, K.G.; Blanchet, L.; Iyer, B. R.; Qusailah, M. S. S. (2007). ”Inspiralling compact binaries in quasi-elliptical orbits: The complete 3PN energy flux”. Physical Review D 77 (6). doi:. https://arxiv.org/abs/0711.0302.
- Ashby, Neil (2002). ”Relativity and the Global Positioning System” (PDF). Physics Today 55 (5): sid. 41–47. doi:. http://www.ipgp.jussieu.fr/~tarantola/Files/Professional/GPS/Neil_Ashby_Relativity_GPS.pdf.
- Ashby, Neil (2003). ”Relativity in the Global Positioning System”. Living Reviews in Relativity 6. doi:. https://link.springer.com/content/pdf/10.12942%2Flrr-2003-1.pdf. Läst 6 juli 2007.
- Ashtekar, Abhay (1986). ”New variables for classical and quantum gravity”. Phys. Rev. Lett. 57 (18): sid. 2244–2247. doi:. PMID 10033673.
- Ashtekar, Abhay (1987). ”New Hamiltonian formulation of general relativity”. Phys. Rev. D36 (6): sid. 1587–1602. doi:.
- Ashtekar, Abhay (2007). ”Loop Quantum Gravity: Four Recent Advances and a Dozen Frequently Asked Questions”. The Eleventh Marcel Grossmann Meeting - on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories - Proceedings of the MG11 Meeting on General Relativity. sid. 126. doi:. ISBN 9789812834263. Bibcode: 2008mgm..conf..126A. https://arxiv.org/abs/0705.2222
- Ashtekar, Abhay; Krishnan, Badri (2004). ”Isolated and Dynamical Horizons and Their Applications”. Living Reviews in Relativity 7. doi:. https://link.springer.com/article/10.12942/lrr-2004-10. Läst 28 augusti 2007.
- Ashtekar, Abhay; Lewandowski, Jerzy (2004). ”Background Independent Quantum Gravity: A Status Report”. Class. Quant. Grav. 21 (15): sid. R53–R152. doi:. https://arxiv.org/abs/gr-qc/0404018.
- Ashtekar, Abhay; Magnon-Ashtekar, Anne (1979). ”On conserved quantities in general relativity”. Journal of Mathematical Physics 20 (5): sid. 793–800. doi:.
- Auyang, Sunny Y. (1995). How is Quantum Field Theory Possible?. Oxford University Press. ISBN 0-19-509345-3
- Bania, T. M.; Rood, R. T.; Balser, D. S. (2002). ”The cosmological density of baryons from observations of 3He+ in the Milky Way”. Nature 415 (6867): sid. 54–57. doi:. PMID 11780112.
- Barack, Leor; Cutler, Curt (2004). ”LISA Capture Sources: Approximate Waveforms, Signal-to-Noise Ratios, and Parameter Estimation Accuracy”. Phys. Rev. D69 (8): sid. 082005. doi:. https://arxiv.org/abs/gr-qc/0310125.
- Bardeen, J. M.; Carter, B.; Hawking, S. W. (1973). ”The Four Laws of Black Hole Mechanics”. Comm. Math. Phys. 31 (2): sid. 161–170. doi:. http://projecteuclid.org/euclid.cmp/1103858973.
- Barish, Barry (2005). ”Towards detection of gravitational waves”. i Florides, P.; Nolan, B.; Ottewil, A.. General Relativity and Gravitation. Proceedings of the 17th International Conference. World Scientific. sid. 24–34. ISBN 981-256-424-1
- Barstow, M; Bond, Howard E.; Holberg, J. B.; Burleigh, M. R.; Hubeny, I.; Koester, D. (2005). ”Hubble Space Telescope Spectroscopy of the Balmer lines in Sirius B”. Mon. Not. Roy. Astron. Soc. 362 (4): sid. 1134–1142. doi:. https://arxiv.org/abs/astro-ph/0506600.
- Bartusiak, Marcia (2000). Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time. Berkley. ISBN 978-0-425-18620-6
- Begelman, Mitchell C.; Blandford, Roger D.; Rees, Martin J. (1984). ”Theory of extragalactic radio sources”. Rev. Mod. Phys. 56 (2): sid. 255–351. doi:.
- Beig, Robert; Chruściel, Piotr T. (2006). ”Stationary black holes”. i Françoise, J.-P.; Naber, G.; Tsou, T.S.. Encyclopedia of Mathematical Physics, Volume 2. Elsevier. sid. 2041. ISBN 0-12-512660-3. Bibcode: 2005gr.qc.....2041B. https://arxiv.org/abs/gr-qc/0502041
- Bekenstein, Jacob D. (1973). ”Black Holes and Entropy”. Phys. Rev. D7 (8): sid. 2333–2346. doi:.
- Bekenstein, Jacob D. (1974). ”Generalized Second Law of Thermodynamics in Black-Hole Physics”. Phys. Rev. D9 (12): sid. 3292–3300. doi:.
- Belinskii, V. A.; Khalatnikov, I. M.; Lifschitz, E. M. (1971). ”Oscillatory approach to the singular point in relativistic cosmology”. Advances in Physics 19 (80): sid. 525–573. doi:.; ryska originalartikeln: Belinsky, V. A.; Lifshits, I. M.; Khalatnikov, E. M. (1970). ”Колебательный Режим Приближения К Особой Точке В Релятивистской Космологии”. Uspekhi Fizicheskikh Nauk (Успехи Физических Наук) 102(3) (11): sid. 463–500.
- Bennett, C. L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S. S.; Page, L.; et al. (2003). ”First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results”. Astrophys. J. Suppl. 148 (1): sid. 1–27. doi:. https://arxiv.org/abs/astro-ph/0302207.
- Berger, Beverly K. (2002). ”Numerical Approaches to Spacetime Singularities”. Living Reviews in Relativity 5. doi:. https://link.springer.com/article/10.12942/lrr-2002-1. Läst 4 augusti 2007.
- Bergström, Lars; Goobar, Ariel (2003). Cosmology and Particle Astrophysics (2nd). Wiley & Sons. ISBN 3-540-43128-4
- Bertotti, Bruno; Ciufolini, Ignazio; Bender, Peter L. (1987). ”New test of general relativity: Measurement of de Sitter geodetic precession rate for lunar perigee”. Physical Review Letters 58 (11): sid. 1062–1065. doi:. PMID 10034329.
- Bertotti, Bruno; Iess, L.; Tortora, P. (2003). ”A test of general relativity using radio links with the Cassini spacecraft”. Nature 425 (6956): sid. 374–376. doi:. PMID 14508481.
- Bertschinger, Edmund (1998). ”Simulations of structure formation in the universe”. Annu. Rev. Astron. Astrophys. 36 (1): sid. 599–654. doi:.
- Birrell, N. D.; Davies, P. C. (1984). Quantum Fields in Curved Space. Cambridge University Press. ISBN 0-521-27858-9
- Blair, David; McNamara, Geoff (1997). Ripples on a Cosmic Sea. The Search for Gravitational Waves. Perseus. ISBN 0-7382-0137-5
- Blanchet, L.; Faye, G.; Iyer, B. R.; Sinha, S. (2008). ”The third post-Newtonian gravitational wave polarisations and associated spherical harmonic modes for inspiralling compact binaries in quasi-circular orbits”. Classical and Quantum Gravity 25 (16): sid. 165003. doi:. https://arxiv.org/abs/0802.1249.
- Blanchet, Luc (2014). ”Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries”. Living Reviews in Relativity 17. doi:. https://link.springer.com/article/10.12942/lrr-2014-2. Läst 30 augusti 2017.
- Blandford, R. D. (1987). ”Astrophysical Black Holes”. i Hawking, Stephen W.; Israel, Werner. 300 Years of Gravitation. Cambridge University Press. sid. 277–329. ISBN 0-521-37976-8
- Börner, Gerhard (1993). The Early Universe. Facts and Fiction. Springer. ISBN 0-387-56729-1
- Brandenberger, Robert H. (2007). ”Conceptual Problems of Inflationary Cosmology and a New Approach to Cosmological Structure Formation”. Inflationary Cosmology. Lecture Notes in Physics. "738". sid. 393. doi:. ISBN 978-3-540-74352-1. Bibcode: 2008LNP...738..393B. https://arxiv.org/abs/hep-th/0701111
- Brans, C. H.; Dicke, R. H. (1961). ”Mach's Principle and a Relativistic Theory of Gravitation”. Physical Review 124 (3): sid. 925–935. doi:.
- Bridle, Sarah L.; Lahav, Ofer; Ostriker, Jeremiah P.; Steinhardt, Paul J. (2003). ”Precision Cosmology? Not Just Yet”. Science 299 (5612): sid. 1532–1533. doi:. PMID 12624255. https://arxiv.org/abs/astro-ph/0303180.
- Bruhat, Yvonne (1962). ”The Cauchy Problem”. i Witten, Louis. Gravitation: An Introduction to Current Research. Wiley. sid. 130. ISBN 978-1-114-29166-9
- Buchert, Thomas (2007). ”Dark Energy from Structure—A Status Report”. General Relativity and Gravitation 40 (2–3): sid. 467–527. doi:. https://arxiv.org/abs/0707.2153.
- Buras, R.; Rampp, M.; Janka, H.-Th.; Kifonidis, K. (2003). ”Improved Models of Stellar Core Collapse and Still no Explosions: What is Missing?”. Phys. Rev. Lett. 90 (24): sid. 241101. doi:. PMID 12857181. https://arxiv.org/abs/astro-ph/0303171.
- Caldwell, Robert R. (2004). ”Dark Energy”. Physics World 17 (5): sid. 37–42.
- Carlip, Steven (2001). ”Quantum Gravity: a Progress Report”. Rept. Prog. Phys. 64 (8): sid. 885–942. doi:. https://arxiv.org/abs/gr-qc/0108040.
- Carroll, Bradley W.; Ostlie, Dale A. (1996). An Introduction to Modern Astrophysics. Addison-Wesley. ISBN 0-201-54730-9
- Carroll, Sean M. (2001). ”The Cosmological Constant”. Living Reviews in Relativity 4. doi:. https://link.springer.com/article/10.12942/lrr-2001-1. Läst 21 juli 2007.
- Carter, Brandon (1979). ”The general theory of the mechanical, electromagnetic and thermodynamic properties of black holes”. i Hawking, S. W.; Israel, W.. General Relativity, an Einstein Centenary Survey. Cambridge University Press. sid. 294–369 och 860–863. ISBN 0-521-29928-4
- Celotti, Annalisa; Miller, John C.; Sciama, Dennis W. (1999). ”Astrophysical evidence for the existence of black holes”. Class. Quant. Grav. 16 (12A): sid. A3–A21. doi:. https://arxiv.org/abs/astro-ph/9912186.
- Chandrasekhar, Subrahmanyan (1983). The Mathematical Theory of Black Holes. Oxford University Press. ISBN 0-19-850370-9
- Charbonnel, C.; Primas, F. (2005). ”The Lithium Content of the Galactic Halo Stars”. Astronomy & Astrophysics 442 (3): sid. 961–992. doi:. https://arxiv.org/abs/astro-ph/0505247.
- Ciufolini, Ignazio; Pavlis, Erricos C. (2004). ”A confirmation of the general relativistic prediction of the Lense-Thirring effect”. Nature 431 (7011): sid. 958–960. doi:. PMID 15496915.
- Ciufolini, Ignazio; Pavlis, Erricos C.; Peron, R. (2006). ”Determination of frame-dragging using Earth gravity models from CHAMP and GRACE”. New Astron. 11 (8): sid. 527–550. doi:.
- Coc, A.; Vangioni‐Flam, Elisabeth; Descouvemont, Pierre; Adahchour, Abderrahim; Angulo, Carmen (2004). ”Updated Big Bang Nucleosynthesis confronted to WMAP observations and to the Abundance of Light Elements”. Astrophysical Journal 600 (2): sid. 544–552. doi:. https://arxiv.org/abs/astro-ph/0309480.
- Cutler, Curt; Thorne, Kip S. (2002). ”An overview of gravitational wave sources”. i Bishop, Nigel; Maharaj, Sunil D.. Proceedings of 16th International Conference on General Relativity and Gravitation (GR16). World Scientific. sid. 4090. ISBN 981-238-171-6. Bibcode: 2002gr.qc.....4090C. https://arxiv.org/abs/gr-qc/0204090
- Dalal, Neal; Holz, Daniel E.; Hughes, Scott A.; Jain, Bhuvnesh (2006). ”Short GRB and binary black hole standard sirens as a probe of dark energy”. Phys.Rev. D74 (6): sid. 063006. doi:. https://arxiv.org/abs/astro-ph/0601275.
- Danzmann, Karsten; Rüdiger, Albrecht (2003). ”LISA Technology – Concepts, Status, Prospects” (PDF). Class. Quant. Grav. 20 (10): sid. S1–S9. doi:. Arkiverad från originalet den 26 september 2007. https://web.archive.org/web/20070926105922/http://www.srl.caltech.edu/lisa/documents/KarstenAlbrechtOverviewCQG20-2003.pdf.
- Donoghue, John F. (1995). ”Introduction to the Effective Field Theory Description of Gravity”. i Cornet, Fernando. Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 juni–1 juli 1995. Singapore: World Scientific. sid. 12024. ISBN 981-02-2908-9. Bibcode: 1995gr.qc....12024D. https://arxiv.org/abs/gr-qc/9512024
- Duff, Michael (1996). ”M-Theory (the Theory Formerly Known as Strings)”. Int. J. Mod. Phys. A11 (32): sid. 5623–5641. doi:. https://arxiv.org/abs/hep-th/9608117.
- Ehlers, Jürgen (1973). ”Survey of general relativity theory”. i Israel, Werner. Relativity, Astrophysics and Cosmology. D. Reidel. sid. 1–125. ISBN 90-277-0369-8
- Ehlers, Jürgen; Falco, Emilio E.; Schneider, Peter (1992). Gravitational lenses. Springer. ISBN 3-540-66506-4
- Ehlers, Jürgen; Lämmerzahl, Claus, reds (2006). Special Relativity—Will it Survive the Next 101 Years?. Springer. ISBN 3-540-34522-1
- Ehlers, Jürgen; Rindler, Wolfgang (1997). ”Local and Global Light Bending in Einstein's and other Gravitational Theories”. General Relativity and Gravitation 29 (4): sid. 519–529. doi:.
- Einstein, Albert (1907). ”Über das Relativitätsprinzip und die aus demselben gezogene Folgerungen” (PDF). Jahrbuch der Radioaktivität und Elektronik 4: sid. 411. http://www.soso.ch/wissen/hist/SRT/E-1907.pdf. Läst 5 maj 2008.
- Einstein, Albert (1915). ”Die Feldgleichungen der Gravitation”. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin: sid. 844–847. http://nausikaa2.mpiwg-berlin.mpg.de/cgi-bin/toc/toc.x.cgi?dir=6E3MAXK4&step=thumb. Läst 12 september 2006.
- Einstein, Albert (1916). ”Die Grundlage der allgemeinen Relativitätstheorie” (PDF). Annalen der Physik 49: sid. 769–822. doi:. Arkiverad från originalet den 29 augusti 2006. https://web.archive.org/web/20060829045130/http://www.alberteinstein.info/gallery/gtext3.html. Läst 14 februari 2016.
- Einstein, Albert (1917). ”Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie”. Sitzungsberichte der Preußischen Akademie der Wissenschaften: sid. 142.
- Ellis, George F R; Van Elst, Henk (1999). Lachièze-Rey, Marc. red. Theoretical and Observational Cosmology: Cosmological models (Cargèse lectures 1998). Kluwer. sid. 1–116. doi:. ISBN 978-0-7923-5946-3. Bibcode: 1999toc..conf....1E. https://arxiv.org/abs/gr-qc/9812046
- Everitt, C. W. F.; Buchman, S.; DeBra, D. B.; Keiser, G. M. (2001). ”Gravity Probe B: Countdown to launch”. i Lämmerzahl, C.; Everitt, C. W. F.; Hehl, F. W.. Gyros, Clocks, and Interferometers: Testing Relativistic Gravity in Space (Lecture Notes in Physics 562). Springer. sid. 52–82. ISBN 3-540-41236-0
- Everitt, C. W. F.; Parkinson, Bradford; Kahn, Bob (2007) (PDF). The Gravity Probe B experiment. Post Flight Analysis—Final Report (Preface and Executive Summary). Project Report: NASA, Stanford University and Lockheed Martin. http://einstein.stanford.edu/content/exec_summary/GP-B_ExecSum-scrn.pdf. Läst 5 augusti 2007.
- Falcke, Heino; Melia, Fulvio; Agol, Eric (2000). ”Viewing the Shadow of the Black Hole at the Galactic Center”. Astrophysical Journal 528 (1): sid. L13–L16. doi:. PMID 10587484. https://arxiv.org/abs/astro-ph/9912263.
- Flanagan, Éanna É.; Hughes, Scott A. (2005). ”The basics of gravitational wave theory”. New J.Phys. 7: sid. 204. doi:. https://arxiv.org/abs/gr-qc/0501041.
- Font, José A. (2003). ”Numerical Hydrodynamics in General Relativity”. Living Reviews in Relativity 6. doi:. https://link.springer.com/article/10.12942/lrr-2003-4. Läst 19 augusti 2007.
- Fourès-Bruhat, Yvonne (1952). ”Théoréme d'existence pour certains systémes d'équations aux derivées partielles non linéaires”. Acta Mathematica 88 (1): sid. 141–225. doi:.
- Frauendiener, Jörg (2004). ”Conformal Infinity”. Living Reviews in Relativity 7. doi:. https://link.springer.com/article/10.12942/lrr-2004-1. Läst 21 juli 2007.
- Friedrich, Helmut (2005). ”Is general relativity 'essentially understood'?”. Annalen der Physik 15 (1–2): sid. 84–108. doi:. https://arxiv.org/abs/gr-qc/0508016.
- Futamase, T.; Itoh, Y. (2006). ”The Post-Newtonian Approximation for Relativistic Compact Binaries”. Living Reviews in Relativity 10. doi:. https://link.springer.com/article/10.12942/lrr-2007-2. Läst 29 februari 2008.
- Gamow, George (1970). My World Line. Viking Press. ISBN 0-670-50376-2
- Garfinkle, David (2007). ”Of singularities and breadmaking”. Einstein Online. Arkiverad från originalet den 10 augusti 2007. https://web.archive.org/web/20070810114535/http://www.einstein-online.info/en/spotlights/singularities_bkl/index.html. Läst 3 augusti 2007.
- Geroch, Robert (1996). ”Partial Differential Equations of Physics”. https://arxiv.org/abs/gr-qc/9602055. Läst 23 september 2017.
- Giulini, Domenico (2005). Special Relativity: A First Encounter. Oxford University Press. ISBN 0-19-856746-4
- Giulini, Domenico (2006a). ”Algebraic and Geometric Structures in Special Relativity”. i Ehlers, Jürgen; Lämmerzahl, Claus. Special Relativity—Will it Survive the Next 101 Years?. Springer. sid. 45–111. ISBN 3-540-34522-1. Bibcode: 2006math.ph...2018G. https://arxiv.org/abs/math-ph/0602018
- Giulini, Domenico (2006b). ”An assessment of current paradigms in the physics of fundamental interactions: Some remarks on the notions of general covariance and background independence”. Approaches to Fundamental Physics (Springer) 721: sid. 105. doi:. https://arxiv.org/abs/gr-qc/0603087.
- Gnedin, Nickolay Y. (2005). ”Digitizing the Universe”. Nature 435 (7042): sid. 572–573. doi:. PMID 15931201.
- Goenner, Hubert F. M. (2004). ”On the History of Unified Field Theories”. Living Reviews in Relativity 7. doi:. https://link.springer.com/article/10.12942/lrr-2004-2. Läst 28 februari 2008.
- Goroff, Marc H.; Sagnotti, augustio (1985). ”Quantum gravity at two loops”. Phys. Lett. 160B (1–3): sid. 81–86. doi:.
- Gourgoulhon, Eric (2007). ”3+1 Formalism and Bases of Numerical Relativity”. https://arxiv.org/abs/gr-qc/0703035. Läst 23 september 2017.
- Gowdy, Robert H. (1971). ”Gravitational Waves in Closed Universes”. Phys. Rev. Lett. 27 (12): sid. 826–829. doi:.
- Gowdy, Robert H. (1974). ”Vacuum spacetimes with two-parameter spacelike isometry groups and compact invariant hypersurfaces: Topologies and boundary conditions”. Annals of Physics 83 (1): sid. 203–241. doi:.
- Green, M. B.; Schwarz, J. H.; Witten, E. (1987). Superstring theory. Volume 1: Introduction. Cambridge University Press. ISBN 0-521-35752-7
- Greenstein, J. L.; Oke, J. B.; Shipman, H. L. (1971). ”Effective Temperature, Radius, and Gravitational Redshift of Sirius B”. Astrophysical Journal 169: sid. 563. doi:.
- Gödel, Kurt (1949). ”An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation”. Rev. Mod. Phys. 21 (3): sid. 447. doi:.
- Hafele, J. C.; Keating, R. E. (14 juli 1972). ”Around-the-World Atomic Clocks: Predicted Relativistic Time Gains”. Science 177 (4044): sid. 166–168. doi:. PMID 17779917.
- Hafele, J. C.; Keating, R. E. (14 juli 1972). ”Around-the-World Atomic Clocks: Observed Relativistic Time Gains”. Science 177 (4044): sid. 168–170. doi:. PMID 17779918.
- Hamber, Herbert W. (2009). Quantum Gravitation - The Feynman Path Integral Approach. Springer Publishing. doi:. ISBN 978-3-540-85292-6
- Havas, P. (1964). ”Four-Dimensional Formulation of Newtonian Mechanics and Their Relation to the Special and the General Theory of Relativity”. Rev. Mod. Phys. 36 (4): sid. 938–965. doi:.
- Hawking, Stephen W. (1966). ”The occurrence of singularities in cosmology”. Proceedings of the Royal Society A294 (1439): sid. 511–521. doi:. http://links.jstor.org/sici?sici=0080-4630%2819661018%29294%3A1439%3C511%3ATOOSIC%3E2.0.CO%3B2-Y.
- Hawking, S. W. (1975). ”Particle Creation by Black Holes”. Communications in Mathematical Physics 43 (3): sid. 199–220. doi:.
- Hawking, Stephen W. (1987). ”Quantum cosmology”. i Hawking, Stephen W.; Israel, Werner. 300 Years of Gravitation. Cambridge University Press. sid. 631–651. ISBN 0-521-37976-8
- Hawking, Stephen W.; Ellis, George F. R. (1973). The large scale structure of space-time. Cambridge University Press. ISBN 0-521-09906-4
- Heckmann, O. H. L.; Schücking, E. (1959). ”Newtonsche und Einsteinsche Kosmologie”. i Flügge, S.. Encyclopedia of Physics. "53". sid. 489
- Heusler, Markus (1998). ”Stationary Black Holes: Uniqueness and Beyond”. Living Reviews in Relativity 1. doi:. https://link.springer.com/article/10.12942/lrr-1998-6. Läst 4 augusti 2007.
- Heusler, Markus (1996). Black Hole Uniqueness Theorems. Cambridge University Press. ISBN 0-521-56735-1
- Hey, Tony; Walters, Patrick (2003). The new quantum universe. Cambridge University Press. ISBN 0-521-56457-3
- Hough, Jim; Rowan, Sheila (2000). ”Gravitational Wave Detection by Interferometry (Ground and Space)”. Living Reviews in Relativity 3. https://link.springer.com/article/10.12942/lrr-2000-3. Läst 21 juli 2007.
- Hubble, Edwin (1929). ”A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae” (PDF). Proc. Nat. Acad. Sci. 15 (3): sid. 168–173. doi:. PMID 16577160. PMC: 522427. http://www.pnas.org/cgi/reprint/15/3/168.pdf.
- Hulse, Russell A.; Taylor, Joseph H. (1975). ”Discovery of a pulsar in a binary system”. Astrophys. J. 195: sid. L51–L55. doi:.
- Ibanez, L. E. (2000). ”The second string (phenomenology) revolution”. Class. Quant. Grav. 17 (5): sid. 1117–1128. doi:. https://arxiv.org/abs/hep-ph/9911499.
- Iorio, L. (2009). ”An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense-Thirring Effect with Satellite Laser Ranging”. Space Sci. Rev. 148 (1–4): sid. 363. doi:. https://arxiv.org/abs/0809.1373.
- Isham, Christopher J. (1994). ”Prima facie questions in quantum gravity”. i Ehlers, Jürgen; Friedrich, Helmut. Canonical Gravity: From Classical to Quantum. Springer. ISBN 3-540-58339-4
- Israel, Werner (1971). ”Event Horizons and Gravitational Collapse”. General Relativity and Gravitation 2 (1): sid. 53–59. doi:.
- Israel, Werner (1987). ”Dark stars: the evolution of an idea”. i Hawking, Stephen W.; Israel, Werner. 300 Years of Gravitation. Cambridge University Press. sid. 199–276. ISBN 0-521-37976-8
- Jaranowski, Piotr; Królak, Andrzej (2005). ”Gravitational-Wave Data Analysis. Formalism and Sample Applications: The Gaussian Case”. Living Reviews in Relativity 8. doi:. https://link.springer.com/article/10.12942/lrr-2005-3. Läst 30 juli 2007.
- Kahn, Bob (1996–2012). ”Gravity Probe B Website”. Stanford University. http://einstein.stanford.edu/. Läst 20 april 2012.
- Kahn, Bob (14 april 2007) (PDF). Was Einstein right? Scientists provide first public peek at Gravity Probe B results (Stanford University Press Release). Stanford University News Service. http://einstein.stanford.edu/content/press_releases/SU/pr-aps-041807.pdf.
- Kamionkowski, Marc; Kosowsky, Arthur; Stebbins, Albert (1997). ”Statistics of Cosmic Microwave Background Polarization”. Phys. Rev. D55 (12): sid. 7368–7388. doi:. https://arxiv.org/abs/astro-ph/9611125.
- Kennefick, Daniel (2005). ”Astronomers Test General Relativity: Light-bending and the Solar Redshift”. i Renn, Jürgen. One hundred authors for Einstein. Wiley-VCH. sid. 178–181. ISBN 3-527-40574-7
- Kennefick, Daniel (2007). ”Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition”. Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005. "0709". sid. 685. Bibcode: 2007arXiv0709.0685K. https://arxiv.org/abs/0709.0685
- Kenyon, I. R. (1990). General Relativity. Oxford University Press. ISBN 0-19-851996-6
- Kochanek, C.S.; Falco, E.E.; Impey, C.; Lehar, J. (2007). ”CASTLES Survey Website”. Harvard-Smithsonian Center for Astrophysics. http://cfa-www.harvard.edu/castles. Läst 21 augusti 2007.
- Komar, Arthur (1959). ”Covariant Conservation Laws in General Relativity”. Phys. Rev. 113 (3): sid. 934–936. doi:.
- Kramer, Michael (2004). Karshenboim, S. G.; Peik, E.. red. Astrophysics, Clocks and Fundamental Constants: Millisecond Pulsars as Tools of Fundamental Physics. "648". Springer. sid. 33–54. doi:. ISBN 978-3-540-21967-5. Bibcode: 2004LNP...648...33K. https://arxiv.org/abs/astro-ph/0405178
- Kramer, M.; Stairs, I. H.; Manchester, R. N.; McLaughlin, M. A.; Lyne, A. G.; Ferdman, R. D.; Burgay, M.; Lorimer, D. R.; et al. (2006). ”Tests of general relativity from timing the double pulsar”. Science 314 (5796): sid. 97–102. doi:. PMID 16973838. https://arxiv.org/abs/astro-ph/0609417.
- Kraus, Ute (1998). ”Light Deflection Near Neutron Stars”. Relativistic Astrophysics. Vieweg. sid. 66–81. ISBN 3-528-06909-0
- Kuchař, Karel (1973). ”Canonical Quantization of Gravity”. i Israel, Werner. Relativity, Astrophysics and Cosmology. D. Reidel. sid. 237–288. ISBN 90-277-0369-8
- Künzle, H. P. (1972). ”Galilei and Lorentz Structures on spacetime: comparison of the corresponding geometry and physics”. Annales de l'Institut Henri Poincaré A 17: sid. 337–362. http://www.numdam.org/item?id=AIHPA_1972__17_4_337_0.
- Lahav, Ofer; Suto, Yasushi (2004). ”Measuring our Universe from Galaxy Redshift Surveys”. Living Reviews in Relativity 7. doi:. https://link.springer.com/article/10.12942/lrr-2004-8. Läst 19 augusti 2007.
- Landgraf, M.; Hechler, M.; Kemble, S. (2005). ”Mission design for LISA Pathfinder”. Class. Quant. Grav. 22 (10): sid. S487–S492. doi:. https://arxiv.org/abs/gr-qc/0411071.
- Lehner, Luis (2001). ”Numerical Relativity: A review”. Class. Quant. Grav. 18 (17): sid. R25–R86. doi:. https://arxiv.org/abs/gr-qc/0106072.
- Lehner, Luis (2002). ”Numerical Relativity: Status and Prospects”. General Relativity and Gravitation - Proceedings of the 16th International Conference. sid. 210. doi:. ISBN 9789812381712. Bibcode: 2002grg..conf..210L. https://arxiv.org/abs/gr-qc/0202055
- Linde, Andrei (1990). Particle Physics and Inflationary Cosmology. Harwood. sid. 3203. ISBN 3-7186-0489-2. Bibcode: 2005hep.th....3203L. https://arxiv.org/abs/hep-th/0503203
- Linde, Andrei (2005). ”Towards inflation in string theory”. J. Phys. Conf. Ser. 24: sid. 151–160. doi:. https://arxiv.org/abs/hep-th/0503195.
- Loll, Renate (1998). ”Discrete Approaches to Quantum Gravity in Four Dimensions”. Living Reviews in Relativity 1. doi:. https://link.springer.com/article/10.12942/lrr-1998-13. Läst 9 mars 2008.
- Lovelock, David (1972). ”The Four-Dimensionality of Space and the Einstein Tensor”. J. Math. Phys. 13 (6): sid. 874–876. doi:.
- Ludyk, Günter (2013). Einstein in Matrix Form (1st). Berlin: Springer. ISBN 9783642357978
- MacCallum, M. (2006). ”Finding and using exact solutions of the Einstein equations”. i Mornas, L.; Alonso, J. D.. A Century of Relativity Physics (ERE05, the XXVIII Spanish Relativity Meeting). "841". American Institute of Physics. sid. 129. doi:. Bibcode: 2006AIPC..841..129M. https://arxiv.org/abs/gr-qc/0601102
- Maddox, John (1998). What Remains To Be Discovered. Macmillan. ISBN 0-684-82292-X
- Mannheim, Philip D. (2006). ”Alternatives to Dark Matter and Dark Energy”. Prog. Part. Nucl. Phys. 56 (2): sid. 340–445. doi:. https://arxiv.org/abs/astro-ph/0505266.
- Mather, J. C.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E.; Fixsen, D. J.; Hewagama, T.; Isaacman, R. B.; Jensen, K. A.; et al. (1994). ”Measurement of the cosmic microwave spectrum by the COBE FIRAS instrument”. Astrophysical Journal 420: sid. 439–444. doi:.
- Mermin, N. David (2005). It's About Time. Understanding Einstein's Relativity. Princeton University Press. ISBN 0-691-12201-6
- Messiah, Albert (1999). Quantum Mechanics. Dover Publications. ISBN 0-486-40924-4
- Miller, Cole (2002). Stellar Structure and Evolution (Lecture notes for Astronomy 606). University of Maryland. http://www.astro.umd.edu/~miller/teaching/astr606/. Läst 25 juli 2007.
- Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973). Gravitation. W. H. Freeman. ISBN 0-7167-0344-0
- Møller, Christian (1952). The Theory of Relativity (3rd). Oxford University Press. https://archive.org/details/theoryofrelativi029229mbp
- Narayan, Ramesh (2006). ”Black holes in astrophysics”. New Journal of Physics 7: sid. 199. doi:. https://arxiv.org/abs/gr-qc/0506078.
- Narayan, Ramesh; Bartelmann, Matthias (1997). ”Lectures on Gravitational Lensing”. https://arxiv.org/abs/astro-ph/9606001. Läst 23 september 2017.
- Narlikar, Jayant V. (1993). Introduction to Cosmology. Cambridge University Press. ISBN 0-521-41250-1
- Nieto, Michael Martin (2006). ”The quest to understand the Pioneer anomaly” (PDF). EurophysicsNews 37 (6): sid. 30–34. doi:. http://www.europhysicsnews.org/articles/epn/pdf/2006/06/epn06604.pdf.
- Nordström, Gunnar (1918). ”On the Energy of the Gravitational Field in Einstein's Theory”. Verhandl. Koninkl. Ned. Akad. Wetenschap. 26: sid. 1238–1245.
- Nordtvedt, Kenneth (2003). ”Lunar Laser Ranging—a comprehensive probe of post-Newtonian gravity”. https://arxiv.org/abs/gr-qc/0301024. Läst 23 september 2017.
- Norton, John D. (1985). ”What was Einstein's principle of equivalence?” (PDF). Studies in History and Philosophy of Science 16 (3): sid. 203–246. doi:. http://www.pitt.edu/~jdnorton/papers/ProfE_re-set.pdf. Läst 11 juni 2007.
- Ohanian, Hans C.; Ruffini, Remo (1994). Gravitation and Spacetime. W. W. Norton & Company. ISBN 0-393-96501-5
- Olive, K. A.; Skillman, E. A. (2004). ”A Realistic Determination of the Error on the Primordial Helium Abundance”. Astrophysical Journal 617 (1): sid. 29–49. doi:. https://arxiv.org/abs/astro-ph/0405588.
- O'Meara, John M.; Tytler, David; Kirkman, David; Suzuki, Nao; Prochaska, Jason X.; Lubin, Dan; Wolfe, Arthur M. (2001). ”The Deuterium to Hydrogen Abundance Ratio Towards a Fourth QSO: HS0105+1619”. Astrophysical Journal 552 (2): sid. 718–730. doi:. https://arxiv.org/abs/astro-ph/0011179.
- Oppenheimer, J. Robert; Snyder, H. (1939). ”On continued gravitational contraction”. Physical Review 56 (5): sid. 455–459. doi:.
- Overbye, Dennis (1999). Lonely Hearts of the Cosmos: the story of the scientific quest for the secret of the Universe. Back Bay. ISBN 0-316-64896-5
- Pais, Abraham (1982). 'Subtle is the Lord...' The Science and life of Albert Einstein. Oxford University Press. ISBN 0-19-853907-X
- Peacock, John A. (1999). Cosmological Physics. Cambridge University Press. ISBN 0-521-41072-X
- Peebles, P. J. E. (1966). ”Primordial Helium abundance and primordial fireball II”. Astrophysical Journal 146: sid. 542–552. doi:.
- Peebles, P. J. E. (1993). Principles of physical cosmology. Princeton University Press. ISBN 0-691-01933-9
- Peebles, P.J.E.; Schramm, D.N.; Turner, E.L.; Kron, R.G. (1991). ”The case for the relativistic hot Big Bang cosmology”. Nature 352 (6338): sid. 769–776. doi:.
- Penrose, Roger (1965). ”Gravitational collapse and spacetime singularities”. Physical Review Letters 14 (3): sid. 57–59. doi:.
- Penrose, Roger (1969). ”Gravitational collapse: the role of general relativity”. Rivista del Nuovo Cimento 1: sid. 252–276.
- Penrose, Roger (2004). The Road to Reality. A. A. Knopf. ISBN 0-679-45443-8
- Penzias, A. A.; Wilson, R. W. (1965). ”A measurement of excess antenna temperature at 4080 Mc/s”. Astrophysical Journal 142: sid. 419–421. doi:.
- Peskin, Michael E.; Schroeder, Daniel V. (1995). An Introduction to Quantum Field Theory. Addison-Wesley. ISBN 0-201-50397-2
- Peskin, Michael E. (2007). ”Dark Matter and Particle Physics”. Journal of the Physical Society of Japan 76 (11): sid. 111017. doi:. https://arxiv.org/abs/0707.1536.
- Poisson, Eric (2004). ”The Motion of Point Particles in Curved Spacetime”. Living Reviews in Relativity 7. doi:. https://link.springer.com/article/10.12942/lrr-2004-6. Läst 13 juni 2007.
- Poisson, Eric (2004). A Relativist's Toolkit. The Mathematics of Black-Hole Mechanics. Cambridge University Press. ISBN 0-521-83091-5
- Polchinski, Joseph (1998a). String Theory Vol. I: An Introduction to the Bosonic String. Cambridge University Press. ISBN 0-521-63303-6
- Polchinski, Joseph (1998b). String Theory Vol. II: Superstring Theory and Beyond. Cambridge University Press. ISBN 0-521-63304-4
- Pound, R. V.; Rebka, G. A. (1959). ”Gravitational Red-Shift in Nuclear Resonance”. Physical Review Letters 3 (9): sid. 439–441. doi:.
- Pound, R. V.; Rebka, G. A. (1960). ”Apparent weight of photons”. Phys. Rev. Lett. 4 (7): sid. 337–341. doi:.
- Pound, R. V.; Snider, J. L. (1964). ”Effect of Gravity on Nuclear Resonance”. Phys. Rev. Lett. 13 (18): sid. 539–540. doi:.
- Rees, Martin (1966). ”Appearance of Relativistically Expanding Radio Sources”. Nature 211 (5048): sid. 468–470. doi:.
- Reissner, H. (1916). ”Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie”. Annalen der Physik 355 (9): sid. 106–120. doi:.
- Remillard, Ronald A.; Lin, Dacheng; Cooper, Randall L.; Narayan, Ramesh (2006). ”The Rates of Type I X-Ray Bursts from Transients Observed with RXTE: Evidence for Black Hole Event Horizons”. Astrophysical Journal 646 (1): sid. 407–419. doi:. https://arxiv.org/abs/astro-ph/0509758.
- Renn, Jürgen, red (2007). The Genesis of General Relativity (4 Volumes). Springer. ISBN 1-4020-3999-9
- Renn, Jürgen, red (2005). Albert Einstein—Chief Engineer of the Universe: Einstein's Life and Work in Context. Wiley-VCH. ISBN 3-527-40571-2
- Reula, Oscar A. (1998). ”Hyperbolic Methods for Einstein's Equations”. Living Reviews in Relativity 1. doi:. https://link.springer.com/article/10.12942/lrr-1998-3. Läst 29 augusti 2007.
- Rindler, Wolfgang (2001). Relativity. Special, General and Cosmological. Oxford University Press. ISBN 0-19-850836-0
- Rindler, Wolfgang (1991). Introduction to Special Relativity. Clarendon Press, Oxford. ISBN 0-19-853952-5
- Robson, Ian (1996). Active galactic nuclei. John Wiley. ISBN 0-471-95853-0
- Roulet, E.; Mollerach, S. (1997). ”Microlensing”. Physics Reports 279 (2): sid. 67–118. doi:. https://arxiv.org/abs/astro-ph/9603119.
- Rovelli, Carlo (2000). ”Notes for a brief history of quantum gravity”. https://arxiv.org/abs/gr-qc/0006061. Läst 23 september 2017.
- Rovelli, Carlo (1998). ”Loop Quantum Gravity”. Living Reviews in Relativity 1. doi:. https://link.springer.com/article/10.12942/lrr-1998-1. Läst 13 mars 2008.
- Schäfer, Gerhard (2004). ”Gravitomagnetic Effects”. General Relativity and Gravitation 36 (10): sid. 2223–2235. doi:. https://arxiv.org/abs/gr-qc/0407116.
- Schödel, R.; Ott, T.; Genzel, R.; Eckart, A.; Mouawad, N.; Alexander, T. (2003). ”Stellar Dynamics in the Central Arcsecond of Our Galaxy”. Astrophysical Journal 596 (2): sid. 1015–1034. doi:. https://arxiv.org/abs/astro-ph/0306214.
- Schutz, Bernard F. (1985). A first course in general relativity. Cambridge University Press. ISBN 0-521-27703-5
- Schutz, Bernard F. (2003). Gravity from the ground up. Cambridge University Press. ISBN 0-521-45506-5
- Schwarz, John H. (2007). ”String Theory: Progress and Problems”. Progress of Theoretical Physics Supplement 170: sid. 214. doi:. https://arxiv.org/abs/hep-th/0702219.
- Schwarzschild, Karl (1916a). ”Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie”. Sitzungsber. Preuss. Akad. D. Wiss.: sid. 189–196.
- Schwarzschild, Karl (1916b). ”Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie”. Sitzungsber. Preuss. Akad. D. Wiss.: sid. 424–434.
- Seidel, Edward (1998). ”Numerical Relativity: Towards Simulations of 3D Black Hole Coalescence”. i Narlikar, J. V.; Dadhich, N.. Gravitation and Relativity: At the turn of the millennium (Proceedings of the GR-15 Conference, held at IUCAA, Pune, India, december 16–21, 1997). IUCAA. sid. 6088. ISBN 81-900378-3-8. Bibcode: 1998gr.qc.....6088S. https://arxiv.org/abs/gr-qc/9806088
- Seljak, Uros̆; Zaldarriaga, Matias (1997). ”Signature of Gravity Waves in the Polarization of the Microwave Background”. Phys. Rev. Lett. 78 (11): sid. 2054–2057. doi:. https://arxiv.org/abs/astro-ph/9609169.
- Shapiro, S. S.; Davis, J. L.; Lebach, D. E.; Gregory, J. S. (2004). ”Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999”. Phys. Rev. Lett. 92 (12): sid. 121101. doi:. PMID 15089661.
- Shapiro, Irwin I. (1964). ”Fourth test of general relativity”. Phys. Rev. Lett. 13 (26): sid. 789–791. doi:.
- Shapiro, I. I.; Pettengill, Gordon; Ash, Michael; Stone, Melvin; Smith, William; Ingalls, Richard; Brockelman, Richard (1968). ”Fourth test of general relativity: preliminary results”. Phys. Rev. Lett. 20 (22): sid. 1265–1269. doi:.
- Singh, Simon (2004). Big Bang: The Origin of the Universe. Fourth Estate. ISBN 0-00-715251-5
- Sorkin, Rafael D. (2005). ”Causal Sets: Discrete Gravity”. i Gomberoff, Andres; Marolf, Donald. Lectures on Quantum Gravity. Springer. sid. 9009. ISBN 0-387-23995-2. Bibcode: 2003gr.qc.....9009S. https://arxiv.org/abs/gr-qc/0309009
- Sorkin, Rafael D. (1997). ”Forks in the Road, on the Way to Quantum Gravity”. Int. J. Theor. Phys. 36 (12): sid. 2759–2781. doi:. https://arxiv.org/abs/gr-qc/9706002.
- Spergel, D. N.; Verde, L.; Peiris, H. V.; Komatsu, E.; Nolta, M. R.; Bennett, C. L.; Halpern, M.; Hinshaw, G.; et al. (2003). ”First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters”. Astrophys. J. Suppl. 148 (1): sid. 175–194. doi:. https://arxiv.org/abs/astro-ph/0302209.
- Spergel, D. N.; Bean, R.; Doré, O.; Nolta, M. R.; Bennett, C. L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; et al. (2007). ”Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology”. Astrophysical Journal Supplement 170 (2): sid. 377–408. doi:. https://arxiv.org/abs/astro-ph/0603449.
- Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos S.; Yoshida, Naoki; Gao, Liang; Navarro, Julio; Thacker, Robert; et al. (2005). ”Simulations of the formation, evolution and clustering of galaxies and quasars”. Nature 435 (7042): sid. 629–636. doi:. PMID 15931216. https://arxiv.org/abs/astro-ph/0504097.
- Stairs, Ingrid H. (2003). ”Testing General Relativity with Pulsar Timing”. Living Reviews in Relativity 6. doi:. https://link.springer.com/article/10.12942/lrr-2003-5. Läst 21 juli 2007.
- Stephani, H.; Kramer, D.; MacCallum, M.; Hoenselaers, C.; Herlt, E. (2003). Exact Solutions of Einstein's Field Equations (2). Cambridge University Press. ISBN 0-521-46136-7
- Synge, J. L. (1972). Relativity: The Special Theory. North-Holland Publishing Company. ISBN 0-7204-0064-3
- Szabados, László B. (2004). ”Quasi-Local Energy-Momentum and Angular Momentum in GR”. Living Reviews in Relativity 7. doi:. https://link.springer.com/article/10.12942/lrr-2004-4. Läst 23 augusti 2007.
- Taylor, Joseph H. (1994). ”Binary pulsars and relativistic gravity”. Rev. Mod. Phys. 66 (3): sid. 711–719. doi:.
- Thiemann, Thomas (2006). Approaches to Fundamental Physics: Loop Quantum Gravity: An Inside View. "721". sid. 185–263. doi:. ISBN 978-3-540-71115-5. Bibcode: 2007LNP...721..185T. https://arxiv.org/abs/hep-th/0608210
- Thiemann, Thomas (2003). Lectures on Loop Quantum Gravity. "631". sid. 41–135. doi:. ISBN 978-3-540-40810-9. https://arxiv.org/abs/gr-qc/0210094
- ’t Hooft, Gerard; Veltman, Martinus (1974). ”One Loop Divergencies in the Theory of Gravitation”. Ann. Inst. Poincare 20: sid. 69.
- Thorne, Kip S. (1972). ”Nonspherical Gravitational Collapse—A Short Review”. i Klauder, J.. Magic without Magic. W. H. Freeman. sid. 231–258
- Thorne, Kip S. (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W W Norton & Company. ISBN 0-393-31276-3
- Thorne, Kip S. (1995). Gravitational radiation. sid. 160. ISBN 0-521-36853-7. Bibcode: 1995pnac.conf..160T. https://arxiv.org/abs/gr-qc/9506086
- Townsend, Paul K. (1997). ”Black Holes (Lecture notes)”. https://arxiv.org/abs/gr-qc/9707012. Läst 23 september 2017.
- Townsend, Paul K. (1996). ”Four Lectures on M-Theory”. https://arxiv.org/abs/hep-th/9612121. Läst 23 september 2017.
- Traschen, Jenny (2000). Bytsenko, A.; Williams, F.. red. An Introduction to Black Hole Evaporation. World Scientific. sid. 180. Bibcode: 2000mmp..conf..180T. https://arxiv.org/abs/gr-qc/0010055
- Trautman, Andrzej (2006). ”Einstein–Cartan theory”. i Françoise, J.-P.; Naber, G. L.; Tsou, S. T.. Encyclopedia of Mathematical Physics, Vol. 2. Elsevier. sid. 189–195. Bibcode: 2006gr.qc.....6062T. https://arxiv.org/abs/gr-qc/0606062
- Unruh, W. G. (1976). ”Notes on Black Hole Evaporation”. Phys. Rev. D 14 (4): sid. 870–892. doi:.
- Valtonen, M. J.; Lehto, H. J.; Nilsson, K.; Heidt, J.; Takalo, L. O.; Sillanpää, A.; Villforth, C.; Kidger, M.; et al. (2008). ”A massive binary black-hole system in OJ 287 and a test of general relativity”. Nature 452 (7189): sid. 851–853. doi:. PMID 18421348. https://arxiv.org/abs/0809.1280.
- Veltman, Martinus (1975). ”Quantum Theory of Gravitation”. i Balian, Roger; Zinn-Justin, Jean. Methods in Field Theory - Les Houches Summer School in Theoretical Physics.. "77". North Holland
- Wald, Robert M. (1975). ”On Particle Creation by Black Holes”. Commun. Math. Phys. 45 (3): sid. 9–34. doi:.
- Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 0-226-87033-2
- Wald, Robert M. (1994). Quantum field theory in curved spacetime and black hole thermodynamics. University of Chicago Press. ISBN 0-226-87027-8
- Wald, Robert M. (2001). ”The Thermodynamics of Black Holes”. Living Reviews in Relativity 4. doi:. https://link.springer.com/article/10.12942/lrr-2001-6. Läst 8 augusti 2007.
- Walsh, D.; Carswell, R. F.; Weymann, R. J. (1979). ”0957 + 561 A, B: twin quasistellar objects or gravitational lens?”. Nature 279 (5712): sid. 381–4. doi:. PMID 16068158.
- Wambsganss, Joachim (1998). ”Gravitational Lensing in Astronomy”. Living Reviews in Relativity 1. doi:. https://link.springer.com/article/10.12942/lrr-1998-12. Läst 20 juli 2007.
- Weinberg, Steven (1972). Gravitation and Cosmology. John Wiley. ISBN 0-471-92567-5
- Weinberg, Steven (1995). The Quantum Theory of Fields I: Foundations. Cambridge University Press. ISBN 0-521-55001-7
- Weinberg, Steven (1996). The Quantum Theory of Fields II: Modern Applications. Cambridge University Press. ISBN 0-521-55002-5
- Weinberg, Steven (2000). The Quantum Theory of Fields III: Supersymmetry. Cambridge University Press. ISBN 0-521-66000-9
- Weisberg, Joel M.; Taylor, Joseph H. (2003). ”The Relativistic Binary Pulsar B1913+16"”. i Bailes, M.; Nice, D. J.; Thorsett, S. E.. Proceedings of "Radio Pulsars," Chania, Crete, augusti, 2002. ASP Conference Series
- Weiss, Achim (2006). ”Elements of the past: Big Bang Nucleosynthesis and observation”. Einstein Online. Max Planck Institute for Gravitational Physics. Arkiverad från originalet den 8 februari 2007. https://web.archive.org/web/20070208212728/http://www.einstein-online.info/en/spotlights/BBN_obs/index.html. Läst 24 februari 2007.
- Wheeler, John A. (1990). A Journey Into Gravity and Spacetime. Scientific American Library. W. H. Freeman. ISBN 0-7167-6034-7
- Will, Clifford M. (1993). Theory and experiment in gravitational physics. Cambridge University Press. ISBN 0-521-43973-6
- Will, Clifford M. (2014). ”The Confrontation between General Relativity and Experiment”. Living Reviews in Relativity 17. doi:. https://link.springer.com/article/10.12942/lrr-2014-4. Läst 21 augusti 2017.
- Zwiebach, Barton (2004). A First Course in String Theory. Cambridge University Press. ISBN 0-521-83143-1
Vidare läsning[redigera | redigera wikitext]
- Populärt
- Einstein, Albert (1997) [1917] (pocket). Den speciella och den allmänna relativitetsteorin (2. uppl.). Göteborg: Daidalos. Libris 7615223. ISBN 9789171730862
- Gustafsson, Bengt (2015). Svarta hål. Teorierna, upptäckterna, människorna. Fri Tanke förlag. ISBN 978-91-87513-39-8
- Sjöstrand, Olof (1971), Einsteins relativitetsteori - Matematisk bakgrund och enkla tillämpningar. Akademiförlaget, Göteborg, Libris 8081544
- Geroch, Robert (1981). General Relativity from A to B. Chicago: University of Chicago Press. ISBN 0-226-28864-1
- Lieber, Lillian (2008). The Einstein Theory of Relativity: A Trip to the Fourth Dimension. Philadelphia: Paul Dry Books, Inc. ISBN 978-1-58988-044-3
- Wald, Robert M. (1992). Space, Time, and Gravity: the Theory of the Big Bang and Black Holes. Chicago: University of Chicago Press. ISBN 0-226-87029-4
- Wheeler, John; Ford, Kenneth (1998). Geons, Black Holes, & Quantum Foam: a life in physics. New York: W. W. Norton. ISBN 0-393- 31991-1
- Inledande studentlitteratur
- Callahan, James J. (2000). The Geometry of Spacetime: an Introduction to Special and General Relativity. New York: Springer. ISBN 0-387-98641-3
- Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes: Introduction to General Relativity. Addison Wesley. ISBN 0-201-38423-X
- Avancerad studentlitteratur
- B. F. Schutz (2009). A First Course in General Relativity (Second Edition). Cambridge University Press. ISBN 978-0-521-88705-2
- Cheng, Ta-Pei (2005). Relativity, Gravitation and Cosmology: a Basic Introduction. Oxford and New York: Oxford University Press. ISBN 0-19-852957-0
- Hartle, James B. (2003). Gravity: an Introduction to Einstein's General Relativity. San Francisco: Addison-Wesley. ISBN 0-8053-8662-9
- Hughston, L. P. & Tod, K. P. (1991). Introduction to General Relativity. Cambridge: Cambridge University Press. ISBN 0-521-33943-X
- d'Inverno, Ray (1992). Introducing Einstein's Relativity. Oxford: Oxford University Press. ISBN 0-19-859686-3
- Ludyk, Günter (2013). Einstein in Matrix Form (1). Berlin: Springer. ISBN 9783642357978
- Litteratur för forskarstuderande
- Carroll, Sean M. (2004). Spacetime and Geometry: An Introduction to General Relativity. San Francisco: Addison-Wesley. ISBN 0-8053-8732-3. http://spacetimeandgeometry.net/
- Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's General Theory of Relativity. New York: Springer. ISBN 978-0-387-69199-2
- Landau, Lev D.; Lifshitz, Evgeny F. (1980). The Classical Theory of Fields (4th ed.). London: Butterworth-Heinemann. ISBN 0-7506-2768-9
- Misner, Charles W.; Thorne, Kip. S.; Wheeler, John A. (1973). Gravitation. W. H. Freeman. ISBN 0-7167-0344-0
- Stephani, Hans (1990). General Relativity: An Introduction to the Theory of the Gravitational Field,. Cambridge: Cambridge University Press. ISBN 0-521-37941-5
- Wald, Robert M. (1984). General Relativity. University of Chicago Press. ISBN 0-226-87033-2
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Allmänna relativitetsteorin.
Wikimedia Commons har media som rör Allmänna relativitetsteorin.- Einstein Online – artiklar om en rad olika aspekter av relativistisk fysik publicerade av Max Planck-institutet för gravitationsfysik (engelska)
- GEO600 – officiell webbplats
- LIGO Scientific Collaboration – officiell webbplats
- Kurser · Föreläsningar · Lektioner
- Einsteins allmänna relativitetsteori (föreläsning av Leonard Susskind inspelad 22 september 2008 vid Stanford University) (engelska)
- Föreläsningsserier om allmänna relativitetsteorin år 2006 vid Institut Henri Poincaré (introduktion/avancerad) (engelska)
- Lektioner om allmänna relativitetsteorin av John C. Baez (engelska)
- Brown, Kevin. ”Reflections on relativity” (på engelska). Mathpages.com. Arkiverad från originalet den 18 december 2015. https://web.archive.org/web/20151218205507/http://mathpages.com/rr/rrtoc.htm. Läst 29 maj 2005.
- Carroll, Sean M.. ”Lecture Notes on General Relativity” (på engelska). http://arxiv.org/abs/gr-qc/9712019. Läst 5 januari 2014.
- Moor, Rafi. ”Understanding General Relativity” (på engelska). Arkiverad från originalet den 28 december 2015. https://web.archive.org/web/20151228173642/http://www.rafimoor.com/english/GRE.htm. Läst 11 juli 2006.
- Waner, Stefan. ”Introduction to Differential Geometry and General Relativity” (på engelska) (PDF). Arkiverad från originalet den 19 april 2015. https://web.archive.org/web/20150419010152/http://www.zweigmedia.com/diff_geom/tc.html. Läst 5 april 2015.
|











