Boolesk algebra
| Logik, Formellt system |
|---|
| Logiska system |
|
|
Boolesk algebra är ursprungligen en överföring av satslogiken till kalkyl, som introducerades av George Boole år 1854. Den är även ekvivalent med mängdalgebran, med operatorerna union, snitt och komplement. Formellt kan en boolesk algebra definieras som ett distributivt lattice, vars alla element har ett komplement.
Ytterligare ett exempel på en boolesk algebra är ringen , där de binära operationerna , och definieras enligt
En boolesk algebra kan uppfattas som en boolesk ring. De är således ekvivalenta begrepp. En boolesk algebra kan omformas till en boolesk ring genom definitionerna
- .
Booles logiska algebra förbättrades och utvecklades vidare av bland andra matematikerna Charles Peirce, Ernst Schröder och Giuseppe Peano, som moderniserade Booles beteckningar och uttryckssätt. Om man i Booles kalkyl låter 0 och 1 representera sanningsvärdena falskt respektive sant och operatorerna + och motsvara konnektiven respektive , fås enligt ovan endast ett undantag från ordinarie räkneregler, nämligen att 1 + 1 = 1.
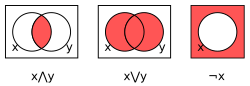
Med venndiagram kan man åskådliggöra de logiska funktionernas sanningsvärden.
Den booleska algebran har tillämpningar bland annat inom områdena digitalteknik, kretskonstruktion, datorer och programkonstruktion.

Den nedre figuren visar booleska funktionsvärdestabeller, kretskonstruktioner och venndiagram för de logiska konnektiven och, eller, materiell implikation och antingen-eller. Det sistnämnda konnektivet motsvaras i algebran av addition modulo 2 och betecknas med symbolen .
Se även[redigera | redigera wikitext]
Källor[redigera | redigera wikitext]
- Whitesitt, J.E., Boolean Algebra and its Applications, Addison-Wesley, 1961.
- von Wright, G.H., Logik, filosofi och språk, Berlingska, Lund, 1957.
- Abbott, J.C., Sets, Lattices and Boolean Algebra, Allyn and Bacon, 1969.
- Bäckström, Karl-Johan, Diskret matematik, Studentlitteratur, 1986.
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Boolesk algebra.
Wikimedia Commons har media som rör Boolesk algebra.
















