Rumtid

Rumtid är en matematisk modell som kombinerar rum och tid till ett enda sammanvävt kontinuum. I sin enklaste form utgår den från ett euklidiskt rum med tre rumsdimensioner och lägger till tiden som en ”fjärde dimension”. Tillsammans bildar de en mångfald som är känd som Minkowskirummet. En punkt i denna fyrdimensionella rumtid kallas för en händelse.
Rumtiden introducerades av den tyske matematikern Hermann Minkowski (1908) som ett sätt att ge en geometrisk beskrivning av de förändringar av tid och rum som Albert Einstein formulerade i sin speciella relativitetsteori (1905). Relativistiska fenomen som längdkontraktion och tidsdilatation kan beskrivas som att olika observatörers koordinatsystem (deras referenssystem) är roterade i förhållande till varandra.
Med den allmänna relativitetsteorin utvidgas rumtidsbegreppet, så att den fyrdimensionella rumtiden kan vara krökt, icke-euklidisk. Under frånvaro av massiva objekt är rumtiden platt, men under påverkan av gravitationskrafter, eller vid accelererande rörelser kröks den och de tidigare räta koordinatlinjerna blir böjda geodetiska linjer. Inom loopkvantgravitation kallar man samma begrepp för rumtidsväv.
Rumtiden i den speciella relativitetsteorin[redigera | redigera wikitext]
Visualisering[redigera | redigera wikitext]

Eftersom det är svårt att tänka sig ett fyrdimensionellt rum avlägsnas ofta för enkelhets skull en av rumsdimensionerna och därmed visualiseras rumtiden med enbart två rumsdimensioner. Skalan på rumsdimensionerna brukar sättas så att ljushastigheten c = 1. Därigenom får exempelvis ett år på tidsaxeln samma längd som ett ljusår på rumsaxlarna.
Händelser[redigera | redigera wikitext]
En händelse på platsen med rumskoordinaterna x och y vid tidpunkten t representeras då av en punkt i ett tredimensionellt koordinatsystem som i bilden till höger. Ett objekt (för enkelhets skull representerat som en enda punkt) som rör sig med konstant hastighet genom rummet kan beskrivas som en rät linje genom rumtiden. Linjens lutning är ett mått på hastigheten – ett objekt i vila representeras av en lodrät linje, och ju fortare objektet rör sig desto mer lutar linjen. Andra typer av rörelser ger andra typer av kurvor. En sådan kurva, som på detta sätt visar objektets position vid alla tidpunkter, kallas för dess världslinje. Punkten A med koordinaterna i bilden till höger visar en sådan händelse och dess världslinje.
Nu[redigera | redigera wikitext]
Vi kan låta origo representera en händelse här och nu. Ljusstrålar som anländer eller utgår från denna händelsepunkt bildar två koner med spetsarna i origo. Med den vedertagna skalan bildar dessa ljuskoner en 45°-vinkel mot axlarna. Punkterna på ljuskonerna representerar fotoner som nu anländer hit och sedan avlägsnar sig igen. Dessa fotoners världslinjer utgör räta linjer som går genom origo och ligger utefter ytan på konerna. De händelser i universum som vi kan se just nu är de som ligger på den nedåtriktade ljuskonen, och omvänt så de händelser i framtiden som kan se vårt nu är de som ligger på den uppåtriktade ljuskonen.
Framtid och dåtid[redigera | redigera wikitext]
Eftersom enligt relativitetsteorin inget massivt objekt kan accelereras till ljusets hastighet, måste världslinjen för ett objekt som befinner sig här och nu ligga innanför dessa koner. Punkter innanför den övre konen representerar objektets tänkbara framtid, och de innanför den undre konen dess möjliga förflutna. Sådana kurvor som ligger innanför dessa koner, och alltså representerar världslinjer för objekt som rör sig med lägre hastighet än ljuset, kallas för tidsliknande kurvor.
Annorstädes[redigera | redigera wikitext]
Punkter som befinner sig utanför konerna representerar händelser som inte är en del av observatörens förflutna eller framtid, och som därför inte är tillgängliga för eller kan påverka denna. Information om dessa händelser når dock observatören så småningom, när ljuskoner som utgår från dem slutligen överlappar den egna ljuskonen. Kurvor som förbinder origo med sådan händelser kan inte utgöra verkliga världslinjer. De representerar snarare rumsdimensioner och kallas för rumsliknande.
Rumtid och Lorentztransformation[redigera | redigera wikitext]

Hur en observatör delar upp rumtiden i rum och tid bestäms av hur observatören rör sig och är därmed olika för två observatörer som rör sig relativt varandra. Sambandet mellan deras koordinater ges av Lorentztransformationens formler och ger upphov till tidsdilatation och längdkontraktion. Bilden till höger visar hur rumtiden förändras för en observatör som färdas med 30 % av ljusets hastighet i x-axelns riktning i förhållande till en annan observatör, sett ur den senares synvinkel. Planen som anger en viss tidpunkt för observatören i rörelse (visade via cirklarna i ljuskonerna) lutar i förhållande till tidsplanen för observatören i vila, och den förras x-axel och tidsaxel är vridna mot varandra jämfört med den stillastående personens axlar. Detta betyder att de båda observatörerna inte är överens om vilka rumslikt separerade händelser som sker samtidigt. Därtill skiljer sig skalorna på de båda observatörernas koordinataxlar åt, så att de inte är överens om storleken på tids- eller längdintervall. Däremot är de båda observatörerna överens om ljuskonernas positioner och orientering.
Minkowskirummet[redigera | redigera wikitext]
Avstånd i rumtiden – rumtidsintervall[redigera | redigera wikitext]
I ett traditionellt tredimensionellt euklidiskt rum definieras avståndet s mellan två punkter A = och B = som:
eller uttryckt på ett annat sätt
I ett fyrdimensionellt Minkowskirum definieras istället för avståndet mellan två punkter i rummet rumtidsintervallet ds mellan två händelser i rumtiden som . Minustecknen i de sista termerna medför att värdet kan bli både positivt och negativt. Ett annat, ålderdomligt sätt att uttrycka detta är att istället för att använda tiden t som den fjärde dimensionen använda det imaginära uttrycket it som enhet. Eftersom i2 = −1 får alla termerna samma signum.
Några egenskaper för rumtidsintervall:
- Händelser mellan vilka intervallet är positivt, ligger i varandras framtid eller förflutna (innanför ljuskonerna). Ett sådant intervall kallas för tidsliknande.
- Intervallets storlek är invariant och oberoende av vem som mäter det och ett mått på den reella tidsdifferensen, som uppmäts av en observatör som ”färdas” mellan händelserna.
- Händelser som ligger på ytan av ljuskonerna har ett intervall som är lika med noll. Ett sådant intervall kallas för ljusliknande.
- Händelser som befinner sig annorstädes, utanför ljuskonerna, har ett negativt rumtidsintervall till utgångspunkten, vilket kallas rumsliknande.
Lorentztransformationen i ett Minkowskirum[redigera | redigera wikitext]
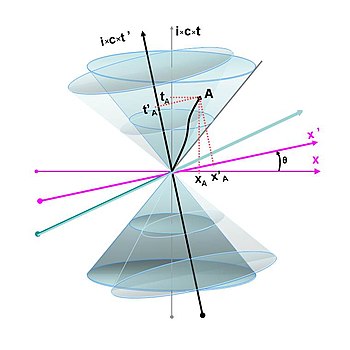
Genom att använda ett Minkowskirum istället för ett vanligt euklidiskt rum blir effekterna av Lorentztransformationen betydligt enklare att åskådliggöra. Istället för den förvrängning som syntes i förra bilden, kommer nu koordinatsystemet för en person i rörelse, att vara roterat i förhållande till en stillastående persons koordinatsystem. Ju större hastighet desto större rotation. Det syns tydligt hur det som ena personen uppfattar som ren tid respektive ren rumsdimension, för den andra personen blir en blandning av rum och tid. Vinkeln θ för denna rotation ges av formeln:
Den allmänna relativitetsteorin och den krökta rumtiden[redigera | redigera wikitext]
I den allmänna relativtetsteorin representeras gravitationen av rumtidens krökning. Fördelningen av massa och energi bestämmer rumtidens krökning enligt Einsteins fältekvationer, och ett föremål som rör sig genom denna rumtid följer den minst krökta linjen, en geodet, genom rumtiden. Geodeten beskriver alltså till exempel den bana som en planet rör sig omkring sin stjärna. Det är värt att notera att i den allmänna relativitetsteorin är rumtiden inte entydigt bestämd av materiens fördelning. Till exempel kan man hitta flera lösningar för ett universum som är tomt på materia och energi. En lösning är naturligtvis Minkowskirummet från den speciella relativitetsteorin, men en annan är Fridman-Robertson-Walker-rummet, som beskriver ett expanderande universum. Detta beror på att lösningen till fältekvationerna kräver begynnelsevillkor eller randvillkor för att vara unik.
Det är inte bara i den allmänna relativitetsteorin som rumtiden är krökt, utan man har även utforskat hur strängteori beter sig rumtider av en högre dimension. Strängteorin formuleras i en tiodimensionell rumtid, och Maldacena har visat att i vissa rumtider som innehåller ett anti-de Sitter-rum[1] så svarar strängteorin mot en konform fältteori i en rumtid av lägre dimension.
Rumtiden och kvantmekaniken[redigera | redigera wikitext]
Det finns problem med att koppla ihop den relativistiska rumtiden med kvantmekaniken, vilket exemplifieras med det så kallade EPR-experimentet, ett tankeexperiment som skapades av Einstein, Podolsky och Rosen. I en enkel form består experimentet av en atom, som är preparerad så att den sänder ut två sammanflätade polariserade fotoner, ljuspartiklar. Att fotonerna är sammanflätade betyder att de båda har kopplade polarisationstillstånd, så att om man genom en mätning bestämmer den ena fotonens polarisation, så vet man också den andra fotonens polarisation. Enligt kvantmekaniken beskrivs de båda fotonerna, då de sänds ut från atomen av en vågfunktion, som beskriver alla möjliga polarisationstillstånd för fotonerna. Då man mäter polarisationstillståndet för den ena fotonen genom att se om den passerar genom ett polarisationsfilter, så kollapsar vågfunktionen och fotonen får en polarisation antingen parallellt med filtrets polarisationsplan, om fotonen passerar, eller vinkelrät mot detsamma om den inte passerar. Då är också polarisationsplanet för den andra fotonen bestämd och man kan beräkna sannolikheten för att den passerar ett polarisationsfilter med en godtycklig orientering av sitt polarisationsplan. Denna sannolikhet är inte densamma som om fotonens polarisationsplan hade varit bestämd i det ögonblick då fotonerna lämnar atomen, vilken ges av Bells teorem. Experiment visar att fotonerna följer den kvantmekaniska fördelningen och inte den sannolikhetsfördelning som ges av Bells teorem, vilket är en utmaning för relativitetsteorin och vår traditionella tolkning av rumtiden, eftersom de två händelserna att man mäter de båda fotonernas polarisation är rumslikt separerade från varandra och därmed inte ens kan förbindas med en ljussignal.[2] Faktum är att två olika observatörer kan ha olika uppfattning om vilken av fotonerna som mättes först och därmed av var kollapsen av vågfunktionen skedde. En tolkning av detta fenomen är att den relativistiska lokaliciteten[3] bryter samman i kvantmekaniken, och de två fotonerna utbyter information snabbare än den kan överföras med ljussignaler, men att detta fenomen inte kan användas för att överföra meddelanden snabbare än ljuset.[4] Kvantmekaniken beskriver alltså en icke-lokal koppling mellan fotonerna, men det är inte en koppling, som ger en perfekt synkronisering mellan fotoner, utan det går att föreställa sig ännu starkare kopplingar.[5] Det är inte bara fotoner som kan vara kvantmekaniskt hopflätade utan detsamma kan gälla andra sorters partiklar. Maldacena med medarbetare har visat att två svarta hål som är hopflätade beter sig som om de är hopkopplade via ett maskhål[6], vilket antyder att man kan betrakta rumtiden i sig själv som en produkt av kvantsammanflätningar. Detta utforskas i ett projekt It from Qubit.[7]
Ett annat problem är hur man ska koppla rumtiden till en kvantiserad gravitationsteori. I dagsläget studeras flera olika metoder för att kvantisera gravitationen såsom supersträngteori och loopkvantgravitation. En del framsteg har gjorts genom att studera hur gravitationen beter sig i en rumtid med bara två rumsdimensioner och en tidsdimension.[8]
Källor[redigera | redigera wikitext]
- ^ Maldacena, J. (1999). ”The large-N limit of superconformal field theories and supergravity”. Int. J. Theor. Phys 38: sid. 1113–1133.
- ^ Albert, David Z. & Galchen, Rivka (2009). ”A quantum threat to special relativity”. Scientific American (March): sid. 26–33.
- ^ Musser, George (2015). ”Where is here?”. Scientific American (November).
- ^ Maudlin, Tim (2011). Quantum non-locality and relativity. Metaphysical intimations of modern physics. 3rd edition. Wiley-Blackwell
- ^ Popescu, Sandu (2014). ”Nonlocality beyond quantum mechanics”. Nature Physics 10 (4): sid. 264–270.
- ^ Maldacena, J (2016). ”Black holes, wormholes and the secrets of quantum spacetime”. Scientific American (November).
- ^ ”It from Qubit”. Simons foundation. https://www.simonsfoundation.org/mathematics-physical-sciences/it-from-qubit/. Läst 17 september 2019.
- ^ Carlip, Steven (2012). ”Quantum gravity in flatland”. Scientific American (April): sid. 30–37.
Vidare läsning[redigera | redigera wikitext]
- Taylor, E. F. & Wheeler, J. A., 1992, Spacetime physics. Introduction to special relativity, Second edition, W. H. Freeman & Co, New York
- Schutz, B. F., 1985, A first course in general relativity, Cambridge University Press
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Rumtid.
Wikimedia Commons har media som rör Rumtid.
| ||||||||||||||||||||
|








