Gyllene snittet
- För andra betydelser, se Gyllene snittet (olika betydelser).
| Gyllene snittet (φ) | |
| Irrationella tal ζ(3) – E – e – γ – δ – φ – √2 – √3 – √5 – π – ρ – ρ – δS – 12√2 | |
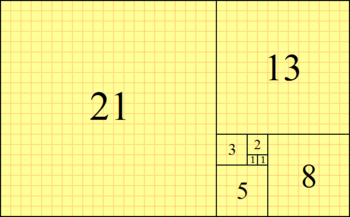 Fibonaccitalen approximerar den gyllene rektangeln, som har sidlängderna 1 och gyllene snittet | |
| Decimalutveckling | 1,61803 39887 49894 84820 45868 ... |
|---|---|

Gyllene snittet, på latin: sectio aurea, är det förhållande som erhålls när en sträcka delas i en längre del a och en kortare del b så att hela sträckan a + b förhåller sig till a som a förhåller sig till b[1]:
Gyllene snittet brukar betecknas med φ (den grekiska bokstaven fi). Det gyllene snittets värde är
Ofta används också det omvända förhållandet 1/φ. Detta värde brukar betecknas med Φ (ett versalt fi):
En rektangel vars sidor förhåller sig som det gyllene snittet kallas den gyllene rektangeln.
Gyllene snittet var känt redan av Pythagoras och de gamla grekerna och genom tiderna, kanske framför allt under renässansen, har man i detta förhållande velat se en norm för den fullkomliga harmonin hos mått och proportioner inom måleriet, fotokonsten, arkitekturen och bildhuggarkonsten.
Förespråkare har också velat se gyllene snittets proportioner i ett stort antal av naturens skapelser, något som dock har ifrågasatts.
Matematikerna i det antika Grekland intresserade sig för det man nu kallar gyllene snittet eftersom värdet ständigt dök upp i olika geometriska figurer och kroppar som pentagrammet och ikosaedern. Upptäckten av förhållandet brukar tillskrivas Pythagoras och hans följeslagare. Dessa hade en regelbunden femhörning, med ett inskrivet regelbundet pentagram, som symbol.
Den första exakta beskrivningen av gyllene snittet återfinns hos Euklides (cirka 300 f.Kr.). I sin Elementa betecknar han uppdelningen av en sträcka i gyllene snittets proportioner som "delning i extrem- och medelförhållande".[2] Begreppet används i lösningen av flera av problemen i Elementa.[3] Euklides beteckning var fram till mitten av 1800-talet den huvudsakligen använda.
Den medeltida matematikern och franciskanermunken Luca Pacioli (1445–1517) betecknar i sitt verk De Divina Proportione, publicerad i Venedig år 1509, det gyllene snittet som "det gudomliga förhållandet". I den andra delen av detta verk avhandlas den romerske arkitekten Vitruvius idéer om den mänskliga kroppens proportioner som utgångspunkt för arkitektur. Skriften innehåller illustrationer av Leonardo da Vinci som undervisades i matematik av Pacioli. I en annan av da Vincis berömda teckningar, den Vitruvianske mannen från runt 1492, kan man hitta ett approximativt gyllene snitt i förhållandet mellan kvadratens sida och cirkelns radie.
Namnet "det gyllene snittet" användes första gången 1835 av Martin Ohm, bror till Georg Ohm i en lärobok i matematik.[4]
Gyllene snittet som skönhetsideal[redigera | redigera wikitext]

Med en början under renässansen har en stor mängd litteratur producerats om gyllene snittets estetiska värde och dess betydelse för utformningen av ideala proportioner inom arkitektur, måleri, skulptur och andra konstnärliga områden. Ett av de första, och kanske det mest inflytelserika verket på detta område var den ovan nämnda La divina proportione av Pacioli. Det har senare ifrågasatts om Pacioli verkligen förespråkade just proportionerna hos gyllene snittet utan snarare var anhängare av Vitruvius system med rationella proportioner.[5]. Oavsett vilket, har hans verk och Da Vincis teckningar haft stort inflytande på efterföljande generationer av konstnärer och arkitekter.
Arkitektur[redigera | redigera wikitext]

Den största av pyramiderna i Giza, Cheopspyramiden, har påståtts approximativt vara en gyllene pyramid, det vill säga en kvadratisk pyramid där höjden på sidoytans triangel och halva basen förhåller sig som φ. En sådan pyramid har en vinkel mellan sidoytan och markplanet på ungefär 51,92°. Olika mätningar har till exempel gett värden på 51,85°[6] och 51,83°,[7] vilket är anmärkningsvärt nära vinkeln i den gyllene pyramiden. Det är dock tveksamt om egyptierna hade de matematiska kunskaper som krävs för att medvetet konstruera en pyramid med sådana proportioner.[8] Så vitt man vet kände de endast till den rätvinkliga triangeln med sidorna i förhållandena 3:4:5 och hade ingen kunskap om Pythagoras sats eller andra möjligheter att resonera kring irrationella förhållanden som φ. De kände till och använde bråk och formler för ett värde på pi, förhållandet mellan en cirkels radie och omkrets, för fyratusen år sedan, så viss matematisk kunskap fanns tidigt hos egyptierna.[9] En pyramid konstruerad utgående från 3:4:5-triangeln skulle ge en lutningsvinkel mellan sidoytan och markplanet på cirka 53,13°, vilket också är ganska nära de uppmätta värdena, och de angivna värden för till exempel pyramidens höjd varierar flera meter i olika källor.[6][10]
Vissa studier av byggnaderna på Atens Akropolis, inklusive Parthenon, har ansett att många av byggnadsverkens proportioner approximativt sammanfaller med gyllene snittet.[11] Detta skulle kunna tyda på att de antika arkitekterna kände till gyllene snittet och medvetet använde sig av dessa proportioner i sina verk. Alternativt, är det möjligt att de bara använde sig av sitt eget omdöme och att detta ledde till just värden som nära sammanföll med gyllene snittet. Å andra sidan kan sentida analyser i efterhand av detta slag kritiseras och ifrågasättas eftersom de lätt påverkas av valet av punkter som man utgår ifrån när man gör mätningarna och slutsatserna därför blir osäkra. Den engelske matematikern Keith Devlin säger
"I själva verket stöds inte det ofta upprepade påståendet att Parthenon i Aten är baserad på gyllene snittets proportioner av verkliga mätningar. Påståendena om grekerna och det gyllene snittet verkar vara utan grund. Det enda vi verkligen vet är att Euklides i sin berömda bok Elementa … visade hur man kunde beräkna dess värde".[12]
Nära samtida källor som Vitruvius, diskuterar uteslutande proportioner som kan uttryckas med hela tal.
Medeltida exempel på byggnadsverk där gyllene snittets proportioner hittats är katedralen i Florens, Notre-Dame i Paris och klosterporten i Lorsch. Det finns dock inte heller här några historiska belägg för att dessa proportioner är avsiktliga. Ett exempel där man vet att gyllene snittet använts medvetet är dock gamla rådhuset i Leipzig från 1556/57, där tornet är asymmetriskt placerat och delar fasadens längd enligt detta förhållande.
Den schweiziske arkitekten och målaren Le Corbusier (1887–1967), utvecklade ett enhetligt mått- och proportionssystem baserat på mänskliga mått och det gyllene snittet. Han offentliggjorde detta system i sin skrift Le Modulor 1948.[13] Han såg sitt system som en vidareutveckling av Vitruvius och Da Vincis tankar. Le Corbusier's Villa Stein i Garches från 1927 är en tillämpning av Modulor-systemet. Husets rektangulära grundplan, fasader och inre struktur är alla utformade enligt gyllene snittets proportioner.[14]
Skulptur[redigera | redigera wikitext]
För världens vackraste kvinna, Venus Milo, ansågs midjans placering i förhållande till hela kroppslängden följa gyllene snittet.
Måleri och fotokonst[redigera | redigera wikitext]


Gyllene snittet tilldelades en nästan magisk betydelse av några renässansteoretiker och utnyttjades i hög grad av vissa målare, i synnerhet Piero della Francesca. Bildytan delas upp enligt formeln 2:3, 3:5, 5:8, 8:13 osv. Det som händer i bilden skall hända i den punkt där Gyllene snittets linjer korsas varvid jämviktsförhållande och harmoni i bilden uppstår. Kompositionen med Gyllene snittet används alltså för att understryka bildinnehållet.
Leonardo da Vincis illustrationer till De Divina Proportione och hans åsikter att gyllene snittet återfinns i många kroppsliga proportioner, har lett till spekulationer om att han använde gyllene snittet i sina egna målningar. Det har till exempel föreslagits att Mona Lisas ansikte skulle vara målat i dessa proportioner.
Gyllene snittet i naturen[redigera | redigera wikitext]
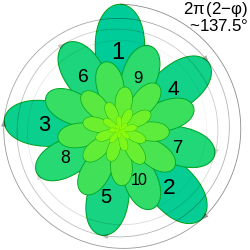
Flera personer, bland annat den tyske filosofen och matematikern Adolf Zeising, har ansett sig finna det gyllene snittets proportioner i många av naturens former.[15] Han ansåg till exempel att naveln delade kroppslängden i detta förhållande, att avståndet upp till naveln i sin tur förhöll sig till avståndet upp till knäet i samma proportion o.s.v. Hans idéer fick stor spridning under 1800-talet och uppfattningen att naturen enligt någon form av naturlag strävade efter sådana proportioner var populär. I praktiken förekommer dock naturligtvis stora variationer i former och proportioner från individ till individ och det är därför diskutabelt om man verkligen kan påvisa gyllene snittets proportioner på detta sätt.
Ett annat exempel på gyllene snittet i naturen är bladens placering och fördelning hos många plantor[källa behövs]. Enligt denna uppfattning växer ofta ett nytt blad ut med en vinkel till föregående blad som är lika med den gyllene vinkeln 137,5°. Exempel på detta växtmönster skulle vara solrosen, olika kål-växters blad, tallbarren på unga tallskott, fjällen på olika kottar, många palm- och Yucca-arter och rosens blomblad[källa behövs]. Därmed får bladen en optimal spridning runt stjälken på så sätt att varje blad hamnar på ett ställe där det skuggas minimalt av övriga blad och växten kan därför utnyttja solljuset på bästa möjliga sätt.[källa behövs]
När till exempel solrosorna har slagit ut vänder de sig mot solen under dagen, så kallad heliotropism. Om man tittar på blomkorgarna ser man att de har spiraler i varsin riktning och antalet spiraler i ena riktningen är större. Antalet spiraler i respektive riktning är vanligen antingen 21 och 34, antingen 34 och 55, antingen 55 och 89, eller 89 och 144[källa behövs]. De hör alla till Fibonaccis talserie: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. (Varje nytt tal i serien är lika med summan av de närmast 2 föregående.) För att optimera utfyllnaden är det nödvändigt för växten att välja det mest passande förhållandet. Förhållandet är exakt gyllene snittet, cirka 1,6180. Motsvarande vinkel, den gyllene vinkeln, är 137,5 grader. Med denna vinkel får man optimal utfyllnad, det vill säga samma utrymme mellan alla fröna. Detta ger en optimal packning av fröna.[källa behövs]
Tillämpningsexempel[redigera | redigera wikitext]

Mer eller mindre medvetna tillämpningar av gyllene snittet:
- Kreditkort enligt ISO 7810-standarden, som till exempel VISA och MasterCard, har ett förhållande mellan sidorna på 1:1,586[16] vilket avviker från den gyllene rektangeln med mindre än 2 %.
- Den civila (tvärskurna) svenska flaggans yttermått har proportionerna 5:8[17].
Beräkning av gyllene snittet[redigera | redigera wikitext]

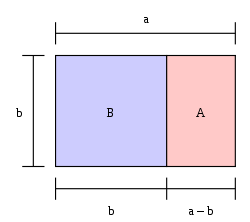
Enligt definitionen av gyllene snittet är
Divideras täljare och nämnare i vänsterledet med erhålls
som ger
vilket är tillåtet, då φ är en kvot mellan två längder och därmed är nollskild. Andragradsekvationen har två reella rötter
- .
vilka approximativt kan skrivas som
Den andra lösningen är uppenbarligen ogiltig, då φ är en kvot mellan längder och måste vara positiv. Icke desto mindre är den intressant, eftersom
En metod som endast utnyttjar heltalsaritmetik, är att beräkna två stora, på varandra följande fibonaccital och dividera dem med varandra. Division mellan till exempel F25001 och F25000, båda mer än 5000-siffriga tal, ger ett approximativt värde på φ med över 10 000 signifikanta siffror.
Matematiska egenskaper[redigera | redigera wikitext]
Geometri[redigera | redigera wikitext]
Pentagonen och pentagrammet[redigera | redigera wikitext]
Som redan de gamla grekerna upptäckte, finns en stark koppling mellan det gyllene snittet och de geometriska figurerna pentagrammet och den regelbundna pentagonen. Förhållandet mellan en diagonal och en kant i en regelbunden pentagon är just φ, det vill säga (se bild).
I pentagrammet kan det gyllene snittet hittas i flera av förhållandena mellan de olika linjerna och kanterna som bygger upp denna symbol (se bild).
Även talet fem dyker ju upp i den matematiska formeln för φ (se ovan).
Ikosaedern[redigera | redigera wikitext]
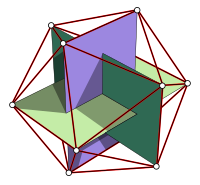
Förhållandet mellan en kant och vissa av diagonalerna i ikosaedern förhåller sig som det gyllene snittet. Detta innebär att man kan tänka sig ikosaedern uppspänd av tre mot varandra vinkelrätt liggande gyllene rektanglar.
Gyllene spiralen[redigera | redigera wikitext]

En gyllene rektangel kan delas in i en kvadrat och en mindre gyllene rektangel. Genom att upprepat dela upp den mindre rektangeln på samma sätt får man en figur i vilken en logaritmisk spiral, den så kallade gyllene spiralen, kan ritas in. Spiralen kan approximeras med en följd av kvartscirklar, en i varje kvadrat.
Gyllene triangeln[redigera | redigera wikitext]

En likbent triangel där den långa sidan förhåller sig till den korta som det gyllene snittet, kallas en gyllene triangel. Sådana trianglar kan bl.a. hittas inskrivna i en regelbunden femhörning. Toppvinkeln i en sådan triangel är 36 grader och basvinklarna 72 grader. En gyllene triangel kan, på liknande sätt som en gyllene rektangel, delas upp i en större triangel och en ytterligare mindre gyllene triangel. Genom att upprepat göra sådana indelningar, får man en serie trianglar genom vars hörnpunkter man kan rita in en gyllene spiral.
Gyllene vinkeln[redigera | redigera wikitext]

Om en cirkel delas in i två vinklar, där den större vinkeln förhåller sig till den mindre som det gyllene snittet, kallas den mindre vinkeln ibland för den gyllene vinkeln och betecknas Ψ. Den gyllene vinkeln är approximativt 137,5 grader. Förhållandet mellan ett helt varv, 360 grader, och den större vinkeln är, på grund av det gyllene snittets egenskaper, också φ.
Samband med Fibonaccitalen[redigera | redigera wikitext]
| n | Fn | kvot Fn / Fn-1 | Avvikelse från φ i procent |
|---|---|---|---|
| 1 | 1 | ||
| 2 | 1 | 1,000000 | -38,1966 |
| 3 | 2 | 2,000000 | 23,6068 |
| 4 | 3 | 1,500000 | -7,2949 |
| 5 | 5 | 1,666667 | 3,00566 |
| 6 | 8 | 1,600000 | -1,11456 |
| 7 | 13 | 1,625000 | 0,43052 |
| 8 | 21 | 1,615385 | -0,16374 |
| 9 | 34 | 1,619048 | 0,06265 |
| 10 | 55 | 1,617647 | -0,02392 |
| 11 | 89 | 1,618182 | 0,00914 |
| 12 | 144 | 1,617977 | -0,00349 |
| 13 | 233 | 1,618056 | 0,00133 |
Kvoten mellan två på varandra följande Fibonaccital (Fn) närmar sig φ då n växer, se tabellen till höger. Detta faktum kan härledas från definitionen av dessa tal: Fn = Fn-1 + Fn-2 vilket ger:
Då n växer mot oändligheten innebär detta att kvoten uppfyller samma samband som gäller för φ nämligen
Ett explicit samband mellan Fibonaccitalen och φ är
Gyllene snittet som det mest irrationella och ädlaste av alla tal[redigera | redigera wikitext]
Gyllene snittet är ett irrationellt tal och kan därmed inte uttryckas exakt med ett bråk, det vill säga en kvot mellan två heltal. I viss mening är det också det tal som sämst kan approximeras med ett bråk. Om man tittar på kedjebråksutvecklingen av φ får man
Att denna utveckling bara innehåller ettor innebär att man vid en trunkering efter ett visst antal termer får största tänkbara rest jämfört med kedjebråksutvecklingen av andra irrationella tal, och det trunkerade uttrycket därmed är en jämförelsevis dålig approximation av det exakta värdet för detta antalet termer i en kedjebråksutveckling. Jämfört till exempel med kedjebråksutvecklingen av π som är
vilket efter bara tre termer ger approximationen 333/106 vilket ger ett närmevärde med fyra riktiga decimaler. Samma antal termer från utvecklingen av φ ger närmevärdet 5/3 = 1.66666... som bara har en riktig decimal. Man kan alltså säga att φ är det tal som svårast låter sig approximeras med ett bråk.
Ekvationen φ2 = 1 + φ ger på motsvarande sätt kvadratrotsutvecklingen
som även den ger förhållandevis dåliga approximationer av φ jämfört med vid utvecklingen av andra irrationella tal.
Andra formler[redigera | redigera wikitext]
En serie för gyllene snittet är[18]
Andra intressanta formler är
Se även[redigera | redigera wikitext]
Referenser[redigera | redigera wikitext]
- Den här artikeln är helt eller delvis baserad på material från tyskspråkiga Wikipedia.
- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia.
Noter[redigera | redigera wikitext]
- ^ ”Goldener Schnitt” (på tyska). Schlag nach!: 100000 Tatsachen aus allen Wissensgebieten. Fachrekationen des Bibliographischen Instituts & Springer-Verlag. 2012. sid. 30
- ^ Euklides, Elementa, Bok 6. definition 3
- ^ till exempel Euklides, Elementa, Bok 2, Proposition XI
- ^ Martin Ohm: Lehrbuch der gesamten höhern Mathematik. Bd 2. Friedrich Volckmar, Leipzig 1835
- ^ Livio, Mario, 2002, The Golden Ratio: The Story of Phi, The World's Most Astonishing Number, Broadway Books, New York, ISBN 0-7679-0815-5
- ^ [a b] Matila Ghyka, The Geometry of Art and Life, New York, Dover, 1977 (pyramidhöjd 148,2m halva basen 116,4m)
- ^ Taylor, The Great Pyramid: Why Was It Built and Who Built It?, 1859 (sidoytans höjd 186,4 m halva basen 115,2 m)
- ^ Eric Temple Bell. The Development of Mathematics, New York: Dover, 1940, s 40
- ^ Emrah Sütcü (14 mars 2024). ”Matematiska genier kämpade för att knäcka pi”. Världens Historia. https://varldenshistoria.se/vetenskap/vem-upptackte-pi. Läst 15 mars 2024.
- ^ Tour Egypt, http://www.touregypt.net/featurestories/greatpyramid1.htm
- ^ Van Mersbergen, Audrey M., "Rhetorical Prototypes in Architecture: Measuring the Acropolis", Philosophical Polemic Communication Quarterly, Vol. 46, 1998.
- ^ Keith J. Devlin The Math Instinct: Why You're A Mathematical Genius (Along With Lobsters, Birds, Cats, And Dogs) New York: Thunder's Mouth Press, 2005, ISBN 1-56025-672-9
- ^ ”Arkiverade kopian”. Arkiverad från originalet den 2 september 2007. https://web.archive.org/web/20070902184146/http://www.fondationlecorbusier.asso.fr/fondationlc.htm. Läst 6 september 2007.
- ^ Le Corbusier, Le Modulor, s 35, citerad i Padova, Richard, Proportion, Science, Philosophy", Architecture, 1999, s 320. Taylor & Francis. ISBN 0-419-22780-6: "Both the paintings and the architectural designs make use of the golden section".
- ^ Zeising, Adolf, Neue Lehre van den Proportionen des meschlischen Körpers, Leipzig, 1854
- ^ ISO/IEC 7810:2003
- ^ lagen (1982:269)
- ^ Brian Roselle, "Golden Mean Series" Arkiverad 25 oktober 2020 hämtat från the Wayback Machine.
Källor[redigera | redigera wikitext]
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Gyllene snittet.
Wikimedia Commons har media som rör Gyllene snittet.
| |||||




























![{\displaystyle \varphi ={\frac {1}{\sqrt[{5}]{-1}}}+{\sqrt[{5}]{-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2e59ccfdcb0aa84fc8e7a22dc776c4f1b434548)