Rotation (avbildning)
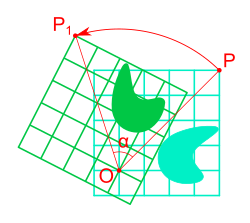
En rotationsmatris är en beskrivning av en linjär avbildning som roterar ett geometriskt objekt.
Sedan början av 1990-talet har transformationer i form av isometrier (det vill säga främst rotationer och translationer) blivit allt viktigare i datorgrafiksammanhang då man söker efterlikna vår vardagliga tredimensionella värld till exempel i spel. Betraktar man ett någorlunda modernt 3D-spel blir det väldigt tydligt. Allteftersom man springer runt i den tredimensionella världen flyttas (roteras) spelfiguren runt i världen.
Rotationer kan realiseras i datorgrafik på flera olika sätt. Två vanliga representationer är via rotationsmatriser och via kvaternioner. Rotationsmatriser lider dock av flera brister, som inte finns i kvaternionrepresentationen. Därför används kvaternioner allt oftare.
Matrisrotation kan anges genom att man använder tre stycken Eulervinklar – en för varje axel – eller med en axel och en rotationsvinkel. Detta tillvägagångssätt för med sig vissa problem.
En typisk rotationsmatris i tre dimensioner är
Den är alltså ett specialfall av en generell rotationsmatris som vid matrismultiplikation roterar en vektor en vinkel kring z-axeln (med andra ord z-axeln är rotationsaxel). Notera att varje rotationsmatris med nödvändighet är ortogonal ty annars blir den omöjligen en isometri och (nästan) omvänt är alla matriser med determinant ett () en rotationsmatris för någon vinkel (specialfallet med translation räknas som rotation med rotationscentrum beläget på oändlighetslinjen).
Så här realiserar man en rotation via kvaternioner: vi specificerar rotationsaxeln (med krav att ) och rotationsvinkel genom att skapa kvaternionen och dess konjugat . All multiplikation nedan är för övrigt kvaternionmultiplikation, som skiljer sig från vanlig multiplikation.
Bilda sedan konjugationsmappningen , där man tänker sig att den helt imaginära kvaternionen representerar den aktuella 3D-punkten (eftersom den är helt imaginär finns det en entydigt förhållande mellan de tre 3D-koordinaterna och kvaternionen ). Då kommer den att rotera punkter (imaginära kvaternioner) en vinkel .
Lägg märke till att konjugatet är detsamma som inversa kvaternionen eftersom vi kräver att , vilket är helt analogt med att matrisen måste vara ortogonal (egentligen ännu mer analogt för unitära matriser och konjugatets betydelse för dessa).
En trevlig egenskap hos kvaternionrotation är att den sammansatta rotationen ges av produkten. Alltså, ska man rotera punkten först med axel och vinkel (kvaternionen) via och sedan med via fås sammansatta rotationen direkt av , där avser kvaternionprodukten av axlarna och vinklarna (kvaternionerna) och .
Externa länkar[redigera | redigera wikitext]
 Wikimedia Commons har media som rör Rotation (avbildning).
Wikimedia Commons har media som rör Rotation (avbildning).
| ||||||||||||||||||||||||||


















